Основы логики

Что такое высказывание?
Какое предложение является высказыванием?
Форма мышления, в которой что-либо утверждается или отрицается.
Высказывание - повествовательное предложение

На какие виды делятся высказывания по своей структуре?
Простые и сложные

Как обозначаются простые высказывания в алгебре логики?
Логическими переменными, которые обозначаются латинскими буквами

Как обозначается истинность таких высказываний?
1 и 0

Сложное
(составное)
высказывание

Что связывает переменные в формулах алгебры высказываний?
Логические операции

Перечислите логические операции
Инверсия (отрицание)
Конъюнкция (умножение)
Дизъюнкция (сложение)
Импликация (следование)
Эквиваленция (равносильность)

Даны простые высказывания
А = "Вчера было пасмурно"
В = "Сегодня ярко светит солнце"
Постройте составное высказывание
" Если вчера было пасмурно, то сегодня ярко светит солнце"
А → B

Переведите на язык алгебры логики сложное высказывание
А = Идёт налево С = Песнь заводит
В = Идёт направо D = Сказку говорит
(A ⇒C)V(B ⇒ D)
… Идёт налево
- песнь заводит,
направо -
сказку говорит…

Переведите сложное высказывание на естественный язык
(А∨В)⇒С
А= «это утро ясное»
В= «это утро теплое»
С=«зонтик не нужен»
Если это утро ясное или теплое, то зонтик не нужен.

Таблицы истинности
Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Алгоритм построения таблицы истинности:
Подсчитать количество переменных n в логическом выражении.
Определить число строк в таблице: m = 2n+ строка заголовка.
Подсчитать количество и установить последовательность выполнения логических операций в формуле с учетом скобок и приоритетов.
Определить количество столбцов в таблице = количество переменных + количество операций.
Заполнить столбцы входных переменных наборами значений.
Провести заполнение таблицы истинности по столбцам, выполняя логические операции в установленной последовательности.

Алгоритм заполнения набора входных переменных:
а) разделить колонку значений первой переменной пополам и заполнить верхнюю часть колонки нулями (ложь), а нижнюю единицами (истина);
б) разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами нулей и единиц, начиная с группы нулей;
в) продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами нулей или единиц до тех пор, пока группы нулей и единиц не будут состоять из одного символа.

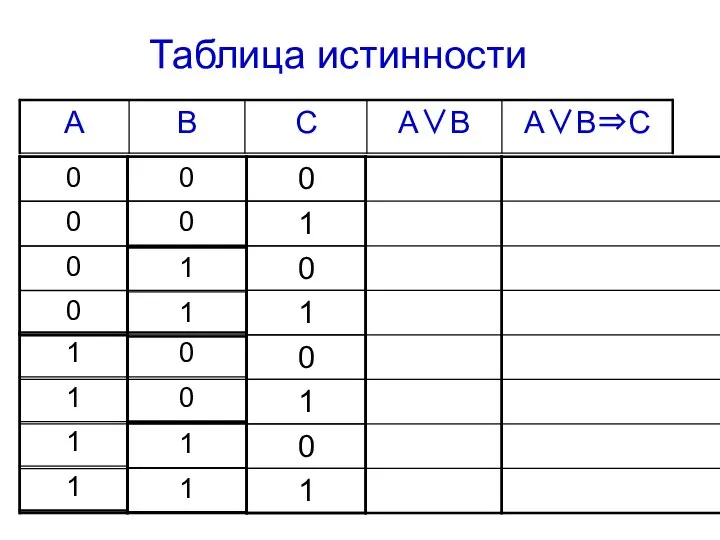
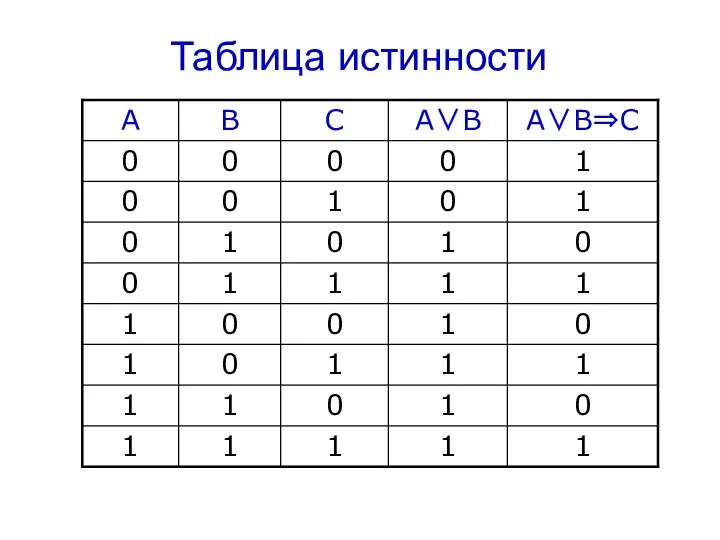
Пример 1.
Определим истинность составного высказывания:
"Если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог".

Переведем высказывание на язык алгебры логики:
A ="купить яблоки"
B ="купить абрикосы"
C ="испечь пирог"
(A v B) → C

Построим таблицу истинности по алгоритму
Сколько переменных? 3
Сколько будет строк? 23=8 + строка на заголовок
Сколько операций в формуле? 2
Подсчитаем количество столбцов в таблице: количество переменных + количество операций 3+2=5

Таблица истинности

Таблица истинности

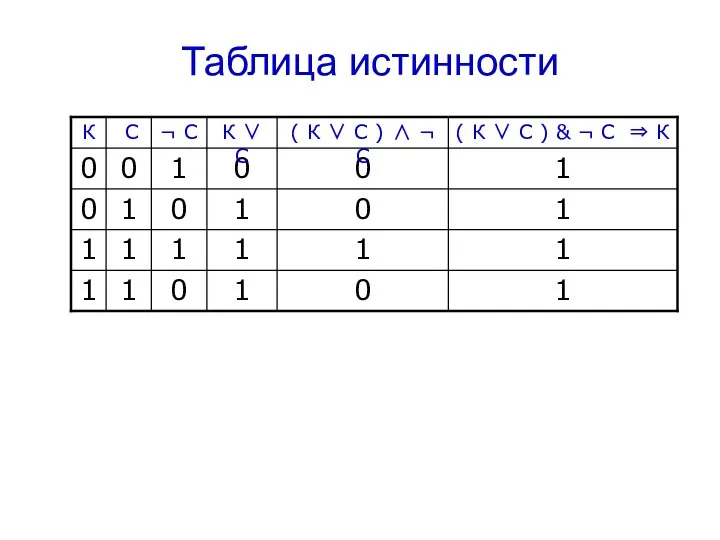
Пример 2. Определим истинность составного высказывания:
В классе оказалось разбито стекло. Учитель объясняет директору: «Это сделал Коля или Саша. Но Саша этого не делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля».

Переведем высказывание на язык алгебры логики:
К = " это сделал Коля "
С = " это сделал Саша "
( К ∨ C ) ∧ ¬ С ⇒ К

Построим таблицу истинности по алгоритму
Сколько переменных? 2
Сколько будет строк? 22=4 + строка на заголовок
Сколько операций в формуле? 4
Подсчитаем количество столбцов в таблице: количество переменных + количество операций 2+4=6

Таблица истинности

Составить таблицы истинности для формул:
а) (А ↔ В) ∧ (¬В → С)
б) А ∧ В ∨ С → (¬А ↔ С)
в) (А ∨ В) ∧ (¬А ∨ С) → (В ↔ С)

Дополнительно:
г) (А ∨ В) ∧ С ↔ ¬В → С
д) А → (В ∧ С ↔ ¬А) ∨ В
е) ((А ↔ В) → ¬(А ∧ С)) ∨ В
ж) ((А ∨ ¬В) → В) ∧ (¬А ∨ В)