Содержание
- 2. Процессор компьютера выполняет арифметические и логические операции над двоичными кодами. И поэтому чтобы иметь представление об
- 3. Логика - это наука о формах и способах мышления. Термин «логика» происходит от древнегреческого logos, означающего
- 4. Первые учения о формах и способах рассуждений возникли в странах Дальнего Востока (Китай, Индия), но в
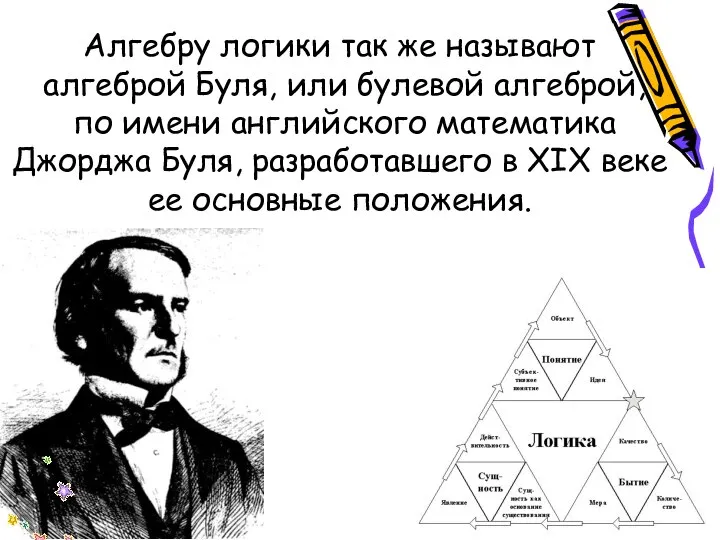
- 5. Алгебру логики так же называют алгеброй Буля, или булевой алгеброй, по имени английского математика Джорджа Буля,
- 6. Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие имеет две стороны: содержание и
- 7. Высказывание (суждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов,
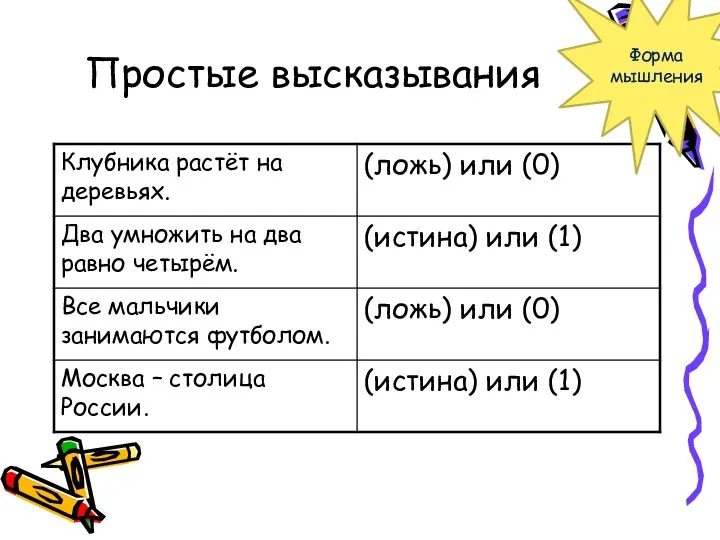
- 8. Простые высказывания Форма мышления
- 9. Простое высказывание состоит из одного высказывания и не содержит логической операции. Составное высказывание содержит высказывания, объединенные
- 10. Сложные высказывания. Форма мышления
- 11. Предикаты Высказывание состоит из понятий, и его можно сравнить с арифметическим выражением. В математической логике рассматриваются
- 12. Умозаключение - это форма мышления, с помощью которой из одного или нескольких высказываний может быть получено
- 13. В качестве основных логических операций в составных высказываниях используются: НЕ (логическое отрицание, инверсия) ИЛИ (логическое сложение,
- 14. Все операции алгебры логики определяются таблицами истинности. Таблица истинности определяет результат выполнения операции для всех возможных
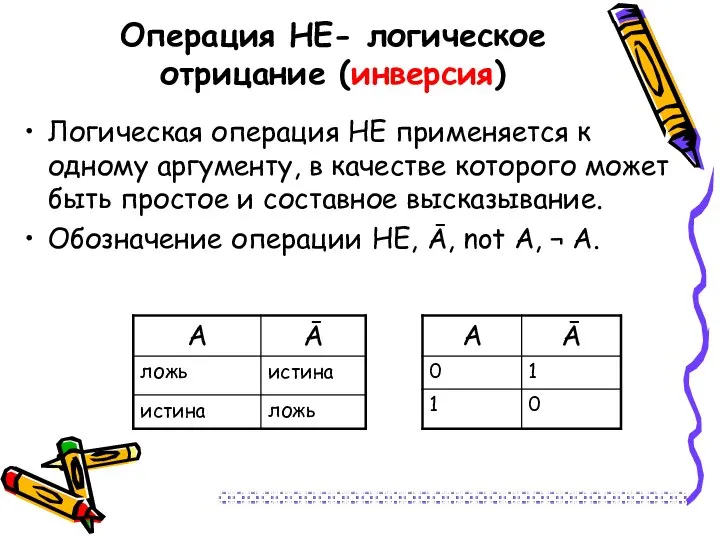
- 15. Операция НЕ- логическое отрицание (инверсия) Логическая операция НЕ применяется к одному аргументу, в качестве которого может
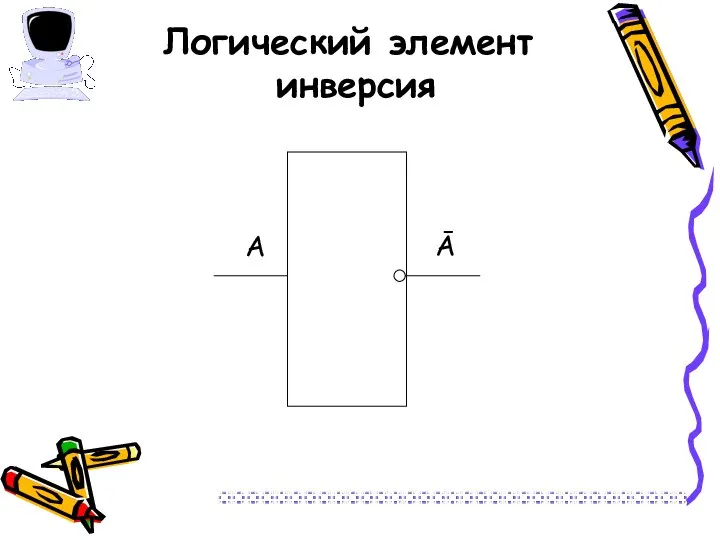
- 16. Логический элемент инверсия
- 17. Операция ИЛИ – логическое сложение (дизъюнкция нестрогая, объединение) Выполняет функцию объединения двух высказываний, в качестве которых
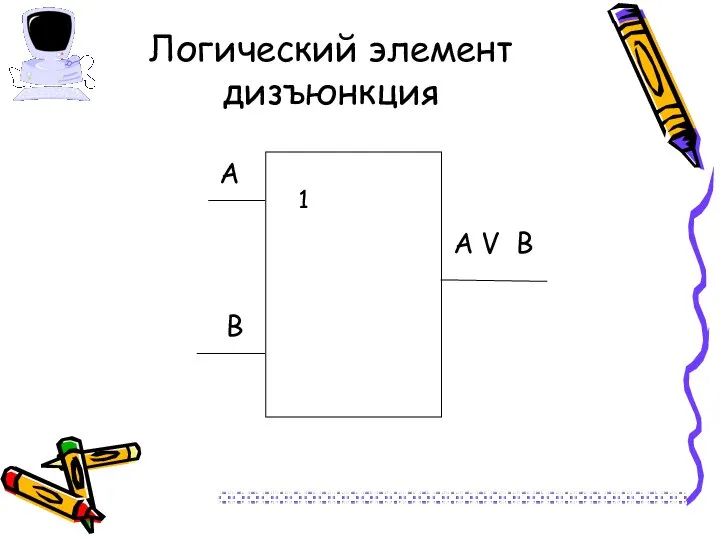
- 18. Логический элемент дизъюнкция
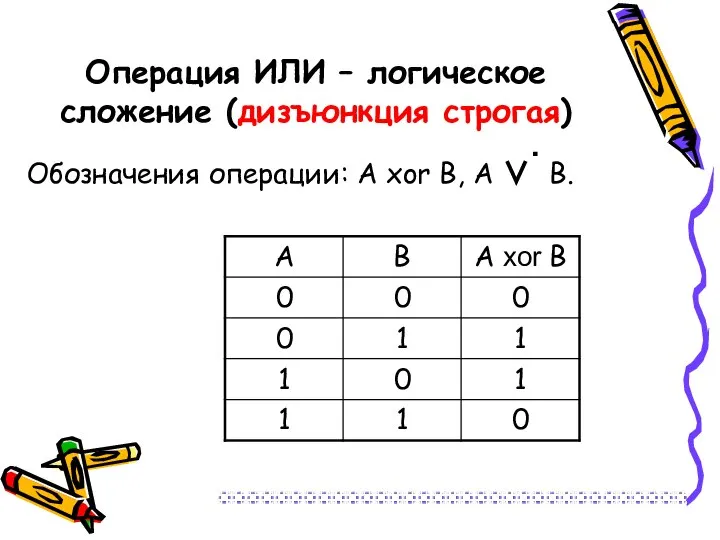
- 19. Операция ИЛИ – логическое сложение (дизъюнкция строгая) Обозначения операции: А xor В, А ∨· В.
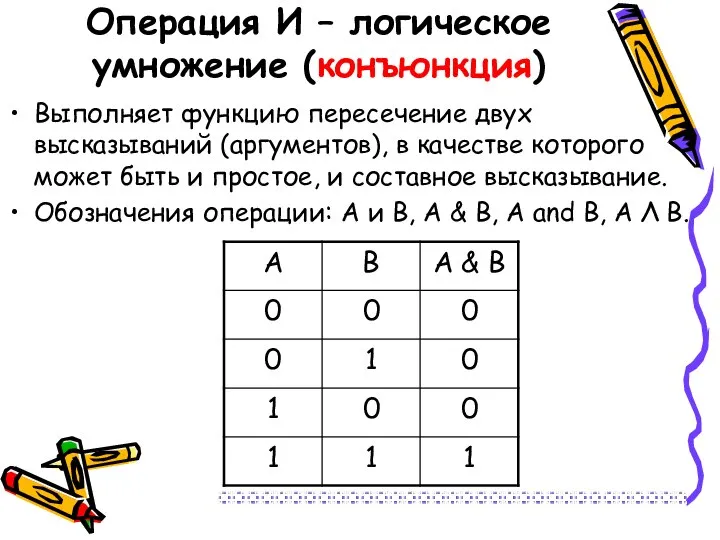
- 20. Операция И – логическое умножение (конъюнкция) Выполняет функцию пересечение двух высказываний (аргументов), в качестве которого может
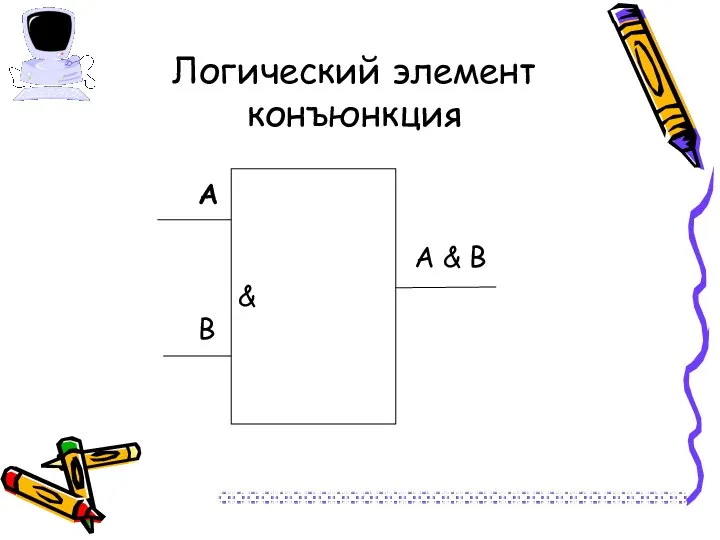
- 21. Логический элемент конъюнкция
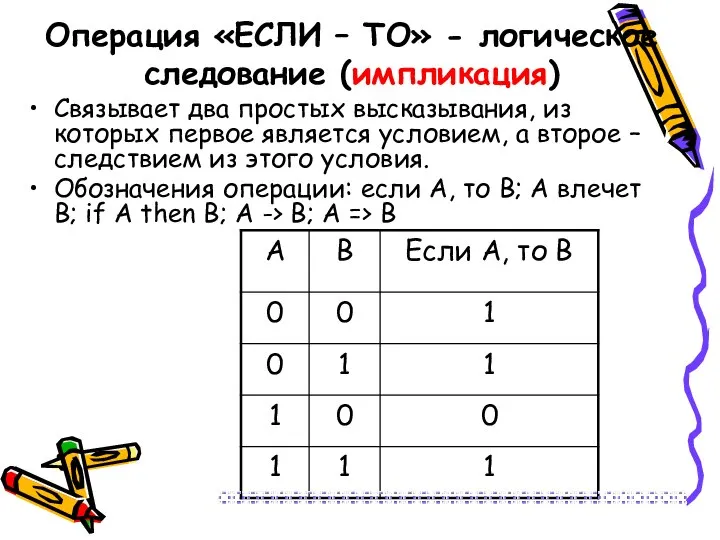
- 22. Операция «ЕСЛИ – ТО» - логическое следование (импликация) Связывает два простых высказывания, из которых первое является
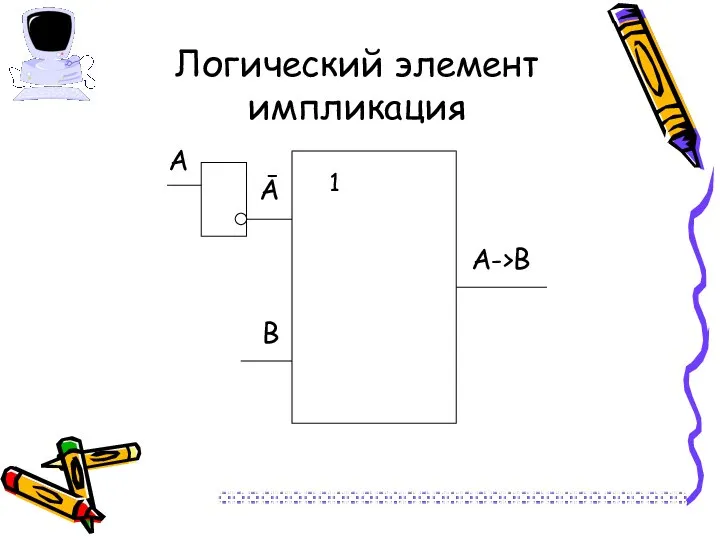
- 23. Логический элемент импликация А
- 24. Операция «А тогда и только тогда, когда В» (эквивалентность, равнозначность) Обозначения операции: А ~ В, А
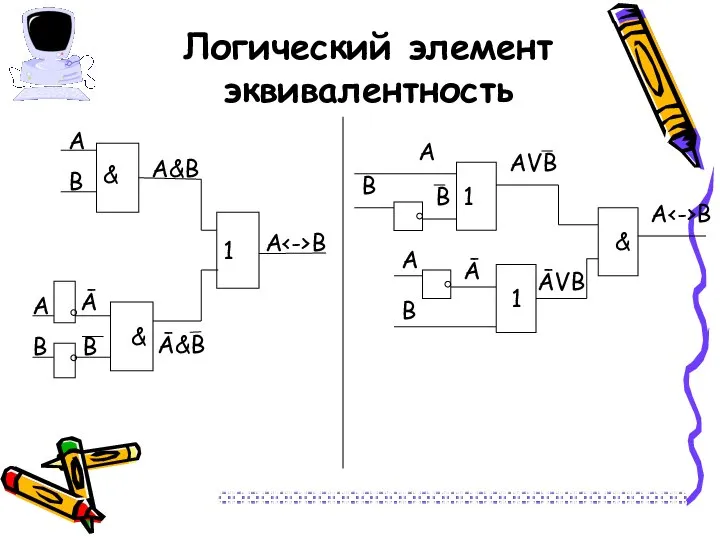
- 25. Логический элемент эквивалентность А В
- 26. Каждое составное высказывание можно выразить в виде формулы (логического выражения). Логическое выражение(формула) – содержит логические переменные,
- 27. Приоритет логических высказываний действия в скобках инверсия конъюнкция дизъюнкция импликация эквивалентность Пример: U ∨ (В ⇒
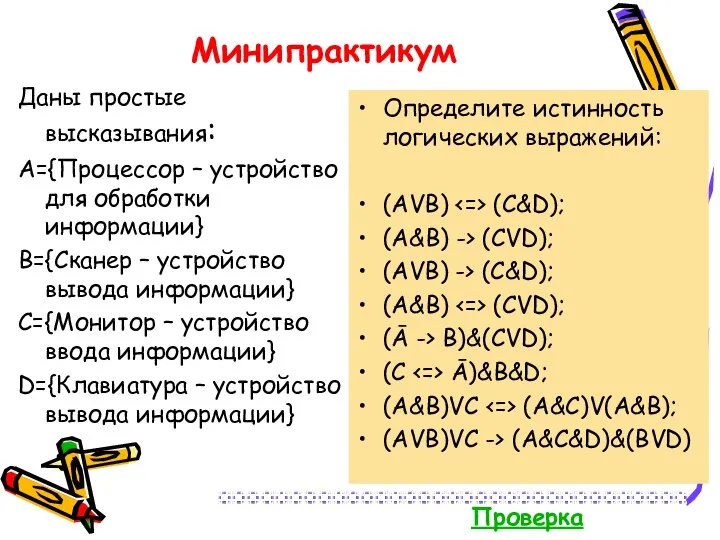
- 28. Минипрактикум Даны простые высказывания: A={Процессор – устройство для обработки информации} B={Сканер – устройство вывода информации} C={Монитор
- 29. Правильные ответы (AVB) (C&D) = 0 (A&B) -> (CVD) = 1 (AVB) -> (C&D) = 0
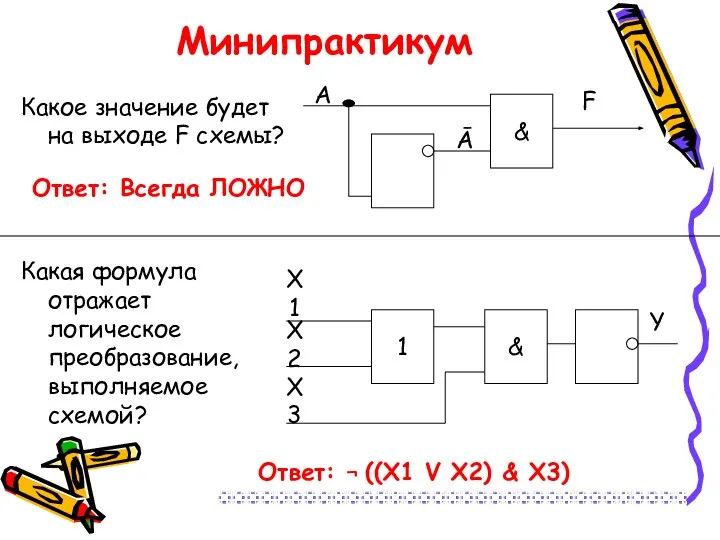
- 30. Ответ: Всегда ЛОЖНО Минипрактикум Какое значение будет на выходе F схемы? Какая формула отражает логическое преобразование,
- 31. Практическая работа ПК Создание в электронных таблицах Microsoft Excel(OpenOffice.org Calc) таблиц истинности логических функций: Конъюнкции Дизъюнкции
- 32. Составление таблиц истинности по логической формуле Количество строк - 2ⁿ, где n- это количество логических переменных
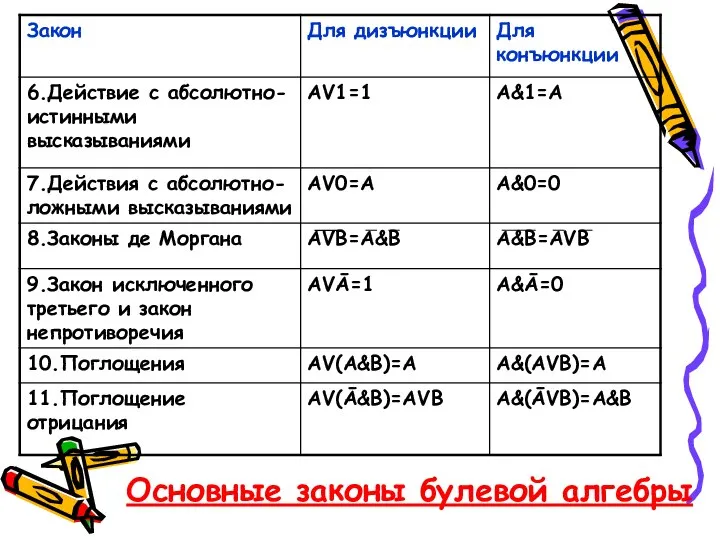
- 33. Основные законы булевой алгебры
- 34. Основные законы булевой алгебры
- 35. Формула склеивания (А В) (А В)=А (А В) (А В)=А
- 36. Формулы поглощения А (А В)= А А (А В)=А А (Ā В)=А В А (Ā В)=А
- 37. Тестовое задание Начать тест
- 38. Вопросы и задания по теме «Основы логики» Зачёт по теме «Основы логики»
- 40. Скачать презентацию























 Логические элементы
Логические элементы ТЗ на интро-заставку
ТЗ на интро-заставку 9-4-3 (1)
9-4-3 (1) Презентация на тему Растровая и векторная графика
Презентация на тему Растровая и векторная графика  Арифметические и логические основы вычислительной техники
Арифметические и логические основы вычислительной техники Создание Web странички - портфолио
Создание Web странички - портфолио Формальная грамматика именования
Формальная грамматика именования Презентация на тему Принципы работы вычислительной техники
Презентация на тему Принципы работы вычислительной техники  Школа Московской биржи. Иркутск, день 2
Школа Московской биржи. Иркутск, день 2 Создание бионического протеза руки с минимальной стоимостью и максимальным функционалом
Создание бионического протеза руки с минимальной стоимостью и максимальным функционалом Кодирование и шифрование
Кодирование и шифрование Программирование на языке Python
Программирование на языке Python Моделирование протокола SNMP с помощью пакета Telelogic TAU SDL
Моделирование протокола SNMP с помощью пакета Telelogic TAU SDL Строки, дата и время в C#. Паттерны GoF. Лекция 4
Строки, дата и время в C#. Паттерны GoF. Лекция 4 Шрифт. Типографика
Шрифт. Типографика Анализ рисков информационной безопасности с помощью нейронных сетей и нечетких когнитивных карт. Лекция 9
Анализ рисков информационной безопасности с помощью нейронных сетей и нечетких когнитивных карт. Лекция 9 3. Formalar
3. Formalar Программное обеспечение. Введение
Программное обеспечение. Введение Запись видео мастер-класса в дистанционной форме
Запись видео мастер-класса в дистанционной форме Представление данных (объекты СУБД)
Представление данных (объекты СУБД) Компьютерная графика
Компьютерная графика Построение отказоустойчивых распределенных систем хранения данных на основе модулярной арифметики
Построение отказоустойчивых распределенных систем хранения данных на основе модулярной арифметики Микропроцессорные устройства. Лекция 4
Микропроцессорные устройства. Лекция 4 Camtasia getting started guide
Camtasia getting started guide Мой ютуб канал и его дальнейшего. Развитие на канале в направление блокинга и гейминга
Мой ютуб канал и его дальнейшего. Развитие на канале в направление блокинга и гейминга Оформление библиографических ссылок к курсовой, дипломной и научным работам
Оформление библиографических ссылок к курсовой, дипломной и научным работам Списки, кортежи
Списки, кортежи Всероссийская образовательная акция Урок цифры — 2020. Нейросети и коммуникации
Всероссийская образовательная акция Урок цифры — 2020. Нейросети и коммуникации