Перевод чисел в системы счисления по разным основаниям

Алгоритм перевода чисел из любой системы счисления в десятичную
Представить число в развернутой форме.
Найти сумму ряда. Полученное число является значением числа в десятичной системе счисления.
Пример: 1011002 = 1 · 25 + 0 · 24 + 1 · 23 + 1 · 22 + 0 · 21 + 0 · 20 =
= 1 · 32 + 0 · 16 + 1 · 8 + 1 · 4 + 0 · 2 + 0 · 1 = 32 + 8 + 4 + 0 = 4410

Алгоритм перевода целых чисел из десятичной системы счисления в любую другую
1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
2. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Пример: 4410 →А2
44/2 │0
22/2│0
11/2│1
5/2 │1
2/2│0
1/2│1 4410 = 1011002

Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2n

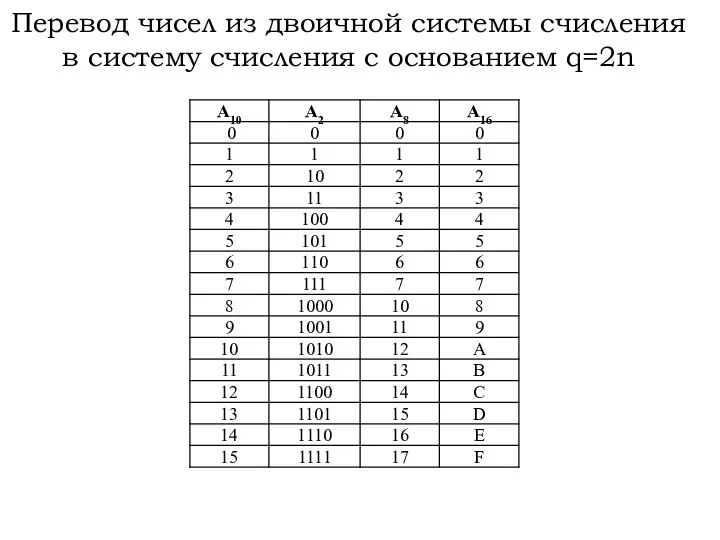
Перевод чисел из двоичной системы счисления в систему счисления с основанием q=2n
Если основание q-ричной системы счисления является степенью числа 2, то перевод чисел из q-ричной систему счисления в 2-ичную и обратно можно проводить по более простым правилам:
1. Двоичное число разбить справа налево на группы по n в каждой.
2. Если в левой последней группе окажется меньше n разрядов, то её надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать её соответствующей цифрой в системе счисления с основанием q=2n
Пример: 11001010011010101112 →А16
0110 0101 0011 0101 0111
6 5 3 5 7 11001010011010101112 = 6535716