Перевод дробных и произвольных чисел из одной системы счисления в другую

Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления числа.
3. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
1. Алгоритм перевода дробных чисел:

Пример 1 Перевести число 0,6562510 в восьмеричную систему счисления.
Получаем: 0,6562510=0,528

Пример 2. Перевести число 0,6562510 в шестнадцатеричную систему счисления.
Получаем: 0,6562510=0,А81

Пример 3. Перевести десятичную дробь 0,562510 в двоичную систему счисления.
Получаем: 0,562510=0,10012

Пример 4. Перевести в двоичную систему счисления десятичную дробь 0.710.

Этот процесс может продолжаться бесконечно, давая все новые и новые знаки в изображении двоичного эквивалента числа 0,710. Так, за четыре шага мы получаем число 0,10112, а за семь шагов число 0,10110012, которое является более точным представлением числа 0,710 в двоичной системе счисления, и т.д. Такой бесконечный процесс обрывают на некотором шаге, когда считают, что получена требуемая точность представления числа.

2. Перевод произвольных чисел
Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа.
Отдельно переводится целая часть, отдельно — дробная.
В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Пример 2.20. Перевести число 17,2510 в двоичную систему счисления.
Получаем: 17,2510=1001,012

Пример 2.21. Перевести число 124,2510 в восьмеричную систему.
Получаем: 124,2510=174,28

Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2n и обратно
Перевод целых чисел. Если основание q-ичной системы счисления является степенью числа 2, то перевод чисел
из q-ичной системы счисления в 2-ичную и обратно можно проводить по более простым правилам. Для того, чтобы целое двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Двоичное число разбить справа налево на группы по n цифр в каждой.
2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.

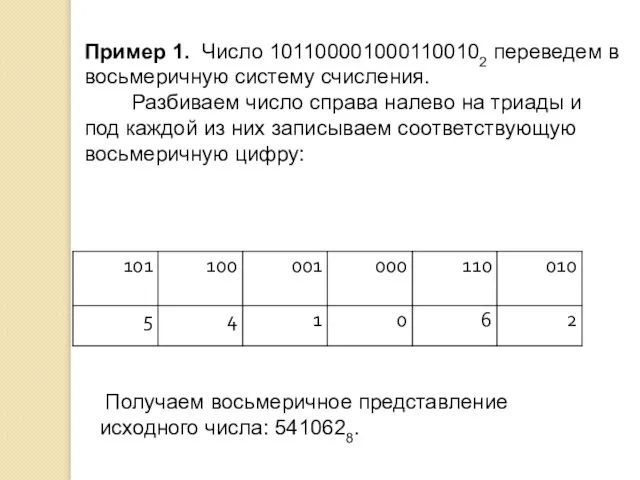
Пример 1. Число 1011000010001100102 переведем в восьмеричную систему счисления.
Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 5410628.

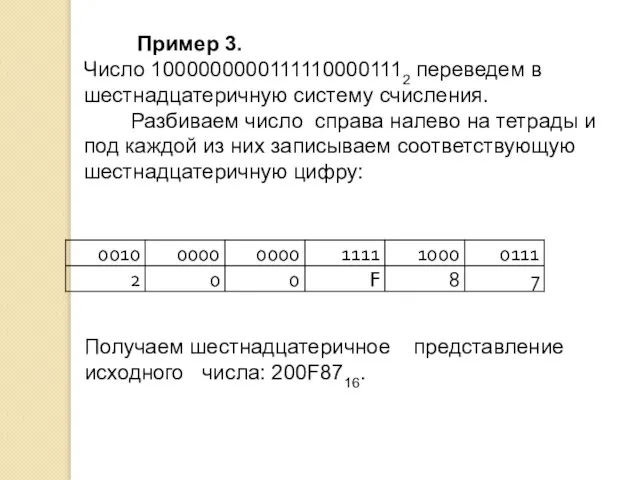
Пример 3.
Число 10000000001111100001112 переведем в шестнадцатеричную систему счисления.
Разбиваем число справа налево на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 200F8716.

Для того, чтобы дробное двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Двоичное число разбить слева направо на группы по n цифр в каждой.
2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Перевод дробных чисел

Пример 2.24. Число 0,101100012 переведем в восьмеричную систему счисления.
Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 0,5428.

Пример 2.25. Число 0,1000000000112 переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 0,80316

Перевод произвольных чисел.
Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой.
2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов;
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n
Пример . Число 111100101,01112 переведем в восьмеричную систему счисления.
Разбиваем целую и дробную части числа на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Получаем восьмеричное представление исходного числа: 745,348.

Пример 2.27. Число 11101001000,110100102 переведем в шестнадцатеричную систему счисления.
Разбиваем целую и дробную части числа на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
Получаем шестнадцатеричное представление исходного числа: 748,D216.
Получаем шестнадцатеричное представление исходного числа: 748,D216.

Перевод чисел из систем счисления с основанием q=2n
в двоичную систему.
Для того, чтобы произвольное число, записанное в системе счисления с основанием q=2n, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-значным эквивалентом в двоичной системе счисления.
Пример 2.28. Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления.
В соответствии с алгоритмом:
Получаем: 10010101100001101012.

Задание:
1. Переведите числа из десятичной системы счисления в восьмеричную:
1) 0,43 2) 37,41 3) 2936 4) 481,625
2. Переведите числа из десятичной системы счисления в шестнадцатеричную:
1) 0,17 2) 43,78 3) 25,25 4) 18,5
4. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):
5 . Переведите двоичные числа в восьмеричную систему счисления:
1) 1010,00100101 2) 1110,01010001 3) 1000,1111001