Содержание
- 2. Схема работы GDCT кодека Исходное изображение 1. Прямое GDCT 2. Квантование 3. Энтропийное кодирование Сжатое представление
- 3. Сжатие информации
- 4. Стратегии сжатия Статистическая стратегия сжатия предполагает определение вероятностей элементов. В блочных методах статистика элементов отдельно кодируется
- 5. Классификация методов сжатия
- 6. Расшифровка названий методов CM (Context modeling) – контекстное моделирование. DMC (Dynamic Marcov compression) – динамическое марковское
- 7. Расшифровка названий методов DC (Distance coding) – кодирование расстояний. IF (Inversion frequencies) – «обратные частоты» (вариант
- 8. Характеристики сжатия а) фактор сжатия r= FS/F0, б) коэффициент сжатия k=F0/FS=1/r , в) качество сжатия η=100(1-r)=100(F0-FS)/FS.
- 9. Энтропия сообщения по К.Шеннону – bps (bit per symbol)
- 10. Теоретический предел длины сжатого сообщения
- 11. Пример расчета энтропии сообщения длины сжатого сообщения и коэффициента сжатия Сообщение : Длинношеее животное Частоты символов
- 12. Пример расчета энтропии сообщения длины сжатого сообщения и коэффициента сжатия Сообщение : 2718281828 Частоты символов Число
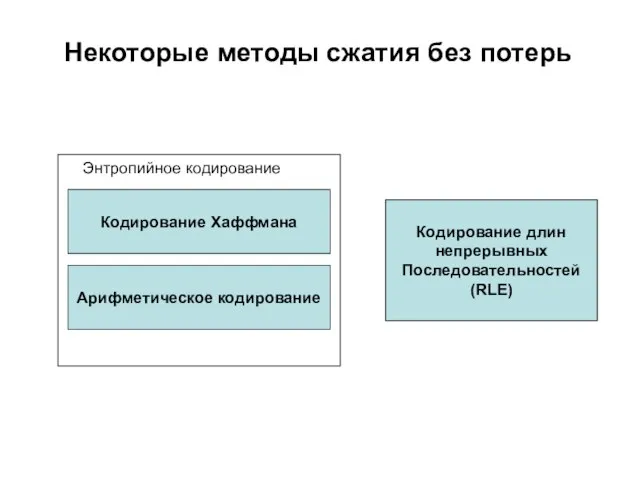
- 13. Некоторые методы сжатия без потерь Кодирование Хаффмана Арифметическое кодирование Кодирование длин непрерывных Последовательностей (RLE) Энтропийное кодирование
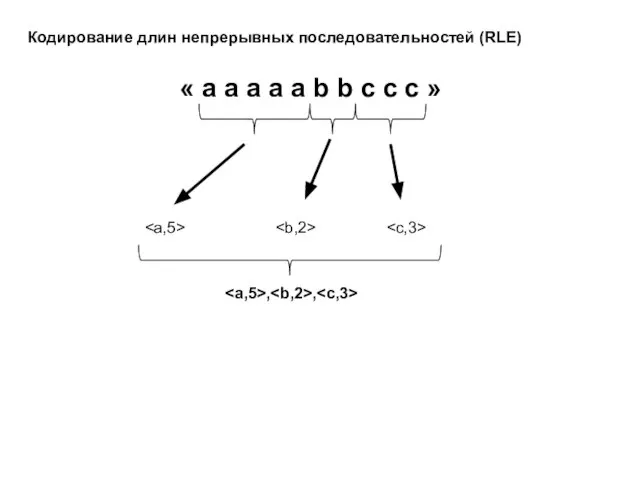
- 14. Кодирование длин непрерывных последовательностей (RLE) « a a a a a b b c c c
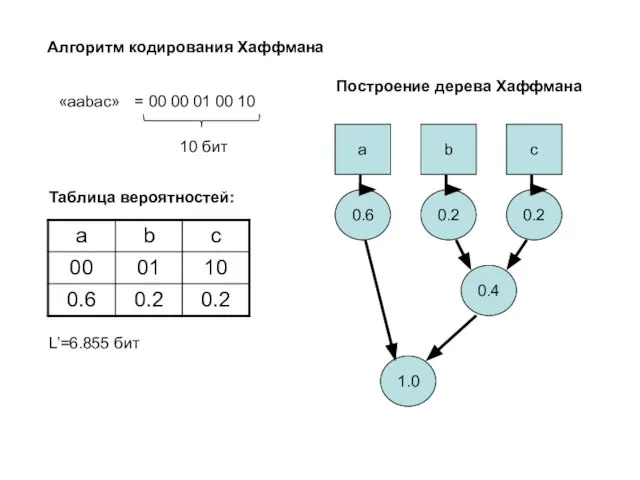
- 15. Алгоритм кодирования Хаффмана «aabac» = 00 00 01 00 10 10 бит Таблица вероятностей: L’=6.855 бит
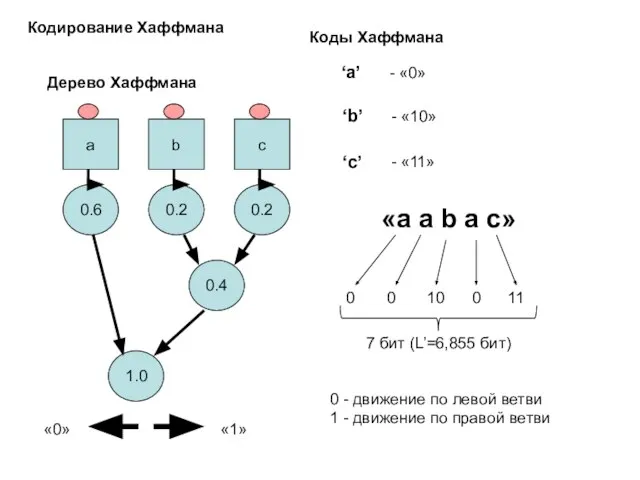
- 16. a b c 0.6 0.2 0.2 0.4 1.0 Дерево Хаффмана «0» «1» ‘a’ - «0» ‘b’
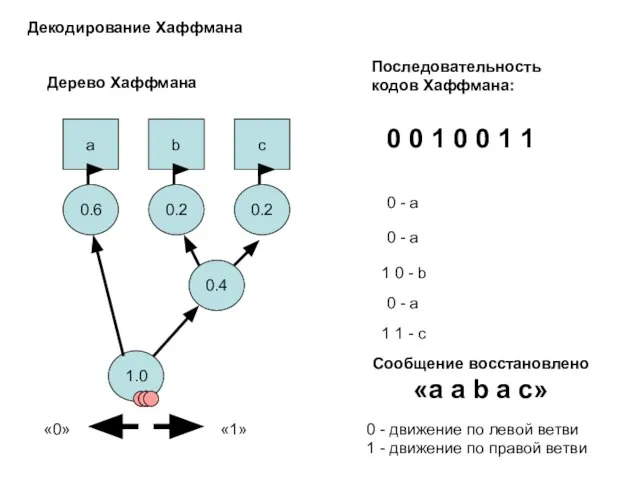
- 17. a b c 0.6 0.2 0.2 0.4 1.0 Дерево Хаффмана «0» «1» Декодирование Хаффмана 0 0
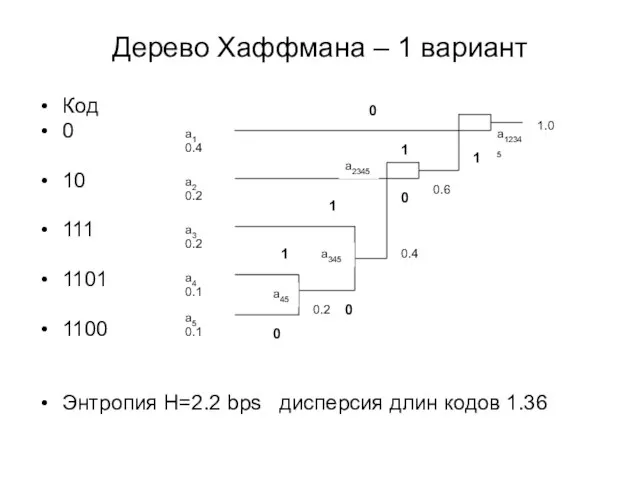
- 18. Дерево Хаффмана – 1 вариант Код 0 10 111 1101 1100 Энтропия Н=2.2 bps дисперсия длин
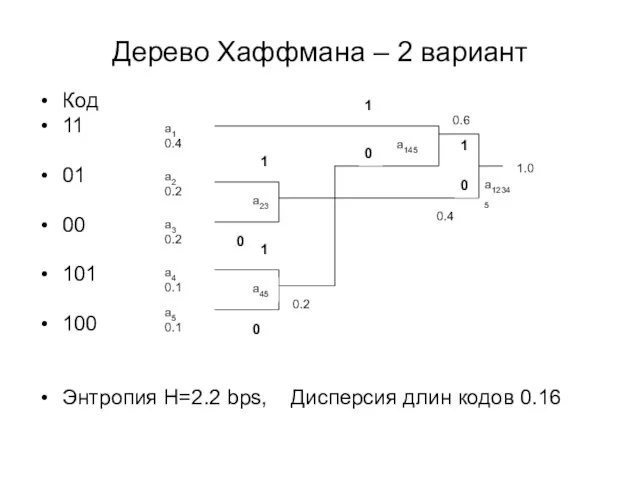
- 19. Дерево Хаффмана – 2 вариант Код 11 01 00 101 100 Энтропия Н=2.2 bps, Дисперсия длин
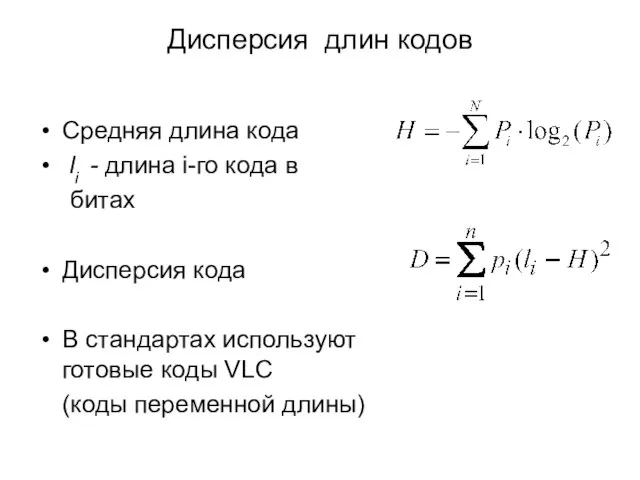
- 20. Дисперсия длин кодов Средняя длина кода li - длина i-го кода в битах Дисперсия кода В
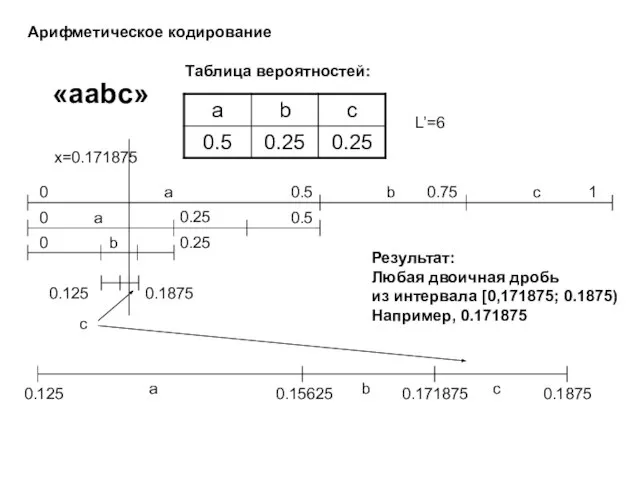
- 21. Арифметическое кодирование «aabc» Таблица вероятностей: Результат: Любая двоичная дробь из интервала [0,171875; 0.1875) Например, 0.171875 L’=6
- 22. Арифметическое кодирование «aabc» Таблица вероятностей: Выходной поток: 0.171875d=0.001011b=«001011» Результат: Любая двоичная дробь из интервала [0,171875; 0.1875)
- 23. Сравнение кодов VLC – удобны для реализации, не универсальны, средняя длина отлична от энтропии Двухпроходные коды
- 24. Исходное изображение «Masha»
- 25. Результат восстановления RLE: 14953 байт (сжатие: 25,29) RLE+Huffman: 11047 байт (сжатие: 34,24) RLE+Arithm: 11022 байт (сжатие:
- 27. Скачать презентацию






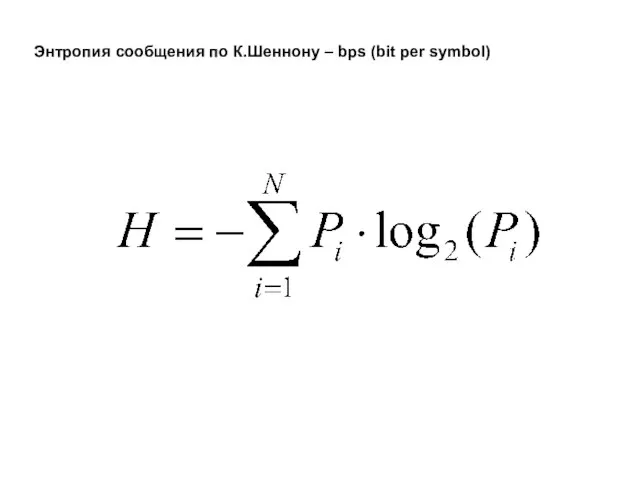







 Основные понятия. Устройство компьютерных систем. Системы счисления
Основные понятия. Устройство компьютерных систем. Системы счисления CD DVD дисководы
CD DVD дисководы Антивирусные программы. Урок 8
Антивирусные программы. Урок 8 Формализация понятия Алгоритм
Формализация понятия Алгоритм Организация вычислений. Относительные, абсолютные и смешанные ссылки
Организация вычислений. Относительные, абсолютные и смешанные ссылки Создание сообщества в ВК
Создание сообщества в ВК Актуальные способы мошенничества и защита от них
Актуальные способы мошенничества и защита от них Ассистент on line проектов
Ассистент on line проектов Несанкционированная рассылка электронных писем
Несанкционированная рассылка электронных писем Батут-арена
Батут-арена Информационные системы и программирование
Информационные системы и программирование Технология программирования на языке Python
Технология программирования на языке Python Методические аспекты эволюции информационных технологий. NBICS-конвергенция
Методические аспекты эволюции информационных технологий. NBICS-конвергенция Указатели. Оператор адреса &
Указатели. Оператор адреса & Умная лента ВК
Умная лента ВК Кодирование информации
Кодирование информации Logowanie do MS Teams
Logowanie do MS Teams Величины. Характеристики величин
Величины. Характеристики величин Принципы защиты персональных данных
Принципы защиты персональных данных Презентация на тему Corel Paint Shop Pro X
Презентация на тему Corel Paint Shop Pro X  История развития средств коммуникации
История развития средств коммуникации Программное обеспечение. Профессия программист
Программное обеспечение. Профессия программист Цикл For
Цикл For Проект Цифровая платформа МАИ
Проект Цифровая платформа МАИ Западное побережье. Автопутешествие
Западное побережье. Автопутешествие Модель текстового документа
Модель текстового документа Программное обеспечение компьютера (ПО)
Программное обеспечение компьютера (ПО) Выбираем вкладку - личный кабинет гражданина
Выбираем вкладку - личный кабинет гражданина