Поиск оптимальных упаковок кругов при помощи алгоритмов оптимизации пакета PyTorch

Введение
Курсовая работа посвящена применению современных методов оптимизации, в частности стохастического градиентного спуска, к задаче поиска оптимальной упаковки кругов.
Цель работы – применить алгоритм стохастического градиентного спуска к задаче об оптимальной упаковке кругов.
Задачи:
Научиться работать с фреймворком PyTorch на базовом уровне;
Улучшить скорость работы алгоритма оптимизации за счет выбора параметров;
Найти процент оптимальных конфигураций, вычисляемых алгоритмом оптимизации;
Максимизировать получаемые значения;
Собрать и проанализировать получаемые данные.

Фреймворк PyTorch
PyTorch — современная библиотека глубокого обучения, разработанная и развивающаяся компанией Facebook. Его разработка началась в 2012 году, но открытым и доступным широкой публике PyTorch стал лишь в 2017 году. С этого момента фреймворк очень быстро набирает популярность и привлекает внимание всё большего числа исследователей.
Тензорные вычисления — основа PyTorch, каркас, вокруг которого наращивается вся остальная функциональность.

Постановка задачи
Задачи упаковки — это класс задач оптимизации в математике, в которых пытаются упаковать объекты в контейнеры. Цель упаковки — либо упаковать отдельный контейнер как можно плотнее, либо упаковать все объекты, использовав как можно меньше контейнеров, либо нахождение конфигурации, которая упаковывает один контейнер с максимальной плотностью. При этом объекты не должны пересекаться и объекты не должны пересекать стены контейнера.
Многие из таких задач могут относиться к упаковке предметов в реальной жизни, вопросам складирования и транспортировки.

Градиентный спуск
Градиентный спуск — это эвристический алгоритм, который выбирает случайную точку, рассчитывает направление скорейшего убывания/возрастания функции (пользуясь градиентом функции в данной точке), а затем пошагово рассчитывает новые значения функции, двигаясь в выбранную сторону. Если убывание/возрастание значения функции становится слишком медленным, алгоритм останавливается и говорит, что нашел минимум.
Градиентный спуск выбирает случайную точку, находит направление самого быстрого убывания функции и двигается до ближайшего минимума вдоль этого направления. Если на каком-то этапе разность между старой точкой (до шага) и новой снижается ниже предела, считается, что минимум найден, алгоритм завершен.

Скорость обучения
Размер шага алгоритма определяет, насколько мы собираемся двигать точку на графике функции потерь, и этот параметр называется «скоростью обучения».
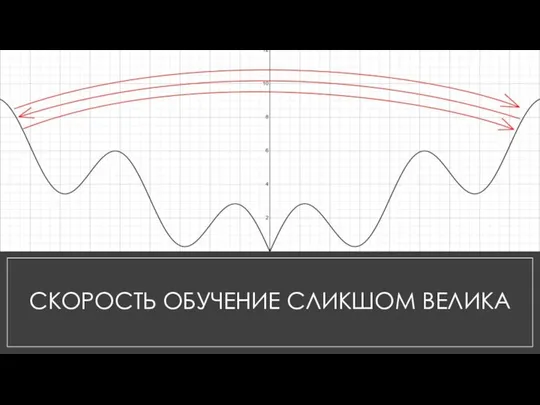
Скорость обучения стоит воспринимать как ширину шагов. В некоторых случаях бывает так, что слишком широкие шаги вообще не позволяют достичь минимума, и машина бесконечно перешагивает через него, затем градиент «разворачивает» ее обратно, и алгоритм снова перескакивает через минимум.
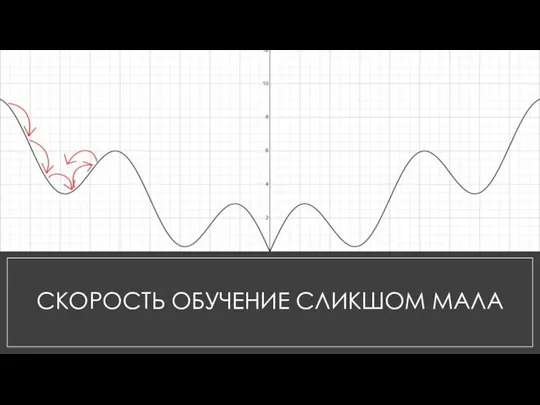
Слишком маленькая скорость обучения тоже может не дать нужного результата, так как можно попасть в локальный минимум, из которого уже не получится выйти.

СКОРОСТЬ ОБУЧЕНИЕ СЛИКШОМ ВЕЛИКА

СКОРОСТЬ ОБУЧЕНИЕ СЛИКШОМ МАЛА

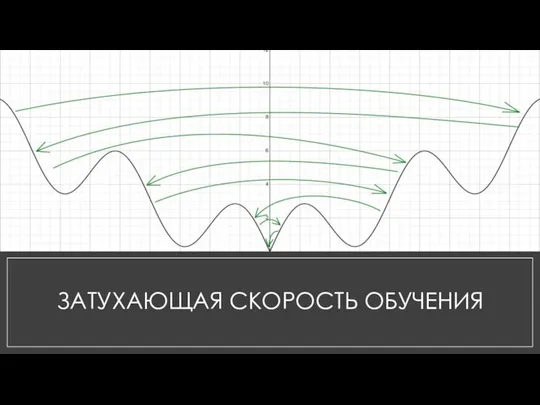
Затухающая скорость обучения
Программа начинает работать с большой скоростью обучения, когда разность между старой точкой и новой перестает меняться или меняется слишком незначительно указанное количество шагов (значение patience), скорость обучения понижается. Таким образом, постепенно доходим до минимума функции.

ЗАТУХАЮЩАЯ СКОРОСТЬ ОБУЧЕНИЯ

Значение patience
При затухающей скорости обучения важно знать, в какой момент нужно уменьшить скорость. Для этого используется значение patience.
Чтобы определить, какое значение даст наилучший результат, было решено провести большое количество запусков программы при разных значениях, при этом подсчитывая среднее арифметическое радиусов кругов и записывая всю полученную информацию в документ. Таким образом получилось выяснить примерные лучшие варианты.

ПРИМЕР ПОЛУЧЕННЫХ ДАННЫХ

Результаты испытаний
По полученным результатам можно сказать, что с ростом количества кругов лучшие результаты получаются на больших значениях patience, но разница между ними уменьшается, поэтому для дальнейших вычислений было выбрано среднее из лучших значений – 320.

Решение задачи
Построим область ( контейнер ) по заданным координатам вершин с помощью уравнений прямых. Далее находим попарно расстояние между центрами кругов, делим на 2 и выбираем наименьшее из них. Находим расстояние от центров кругов до сторон квадрата. Выбираем наименьшее значение из двух полученных, оно и будет является новым радиусом кругов. Далее сдвигаем центры кругов и повторяем тот же алгоритм, таким образом на n-ном шаге находим лучшее значение радиуса.
В программе реализуем этот же алгоритм, с использованием тензоров.

ПРИМЕР ВЫПОЛНЕНИЯ

ПРИМЕР ВЫПОЛНЕНИЯ

ПРИМЕР ВЫПОЛНЕНИЯ

Результаты
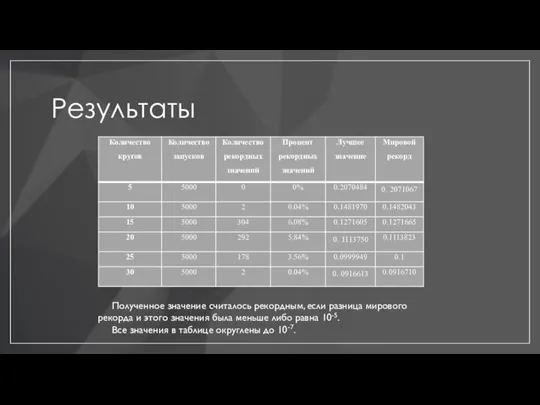
Полученное значение считалось рекордным, если разница мирового рекорда и этого значения была меньше либо равна 10-5.
Все значения в таблице округлены до 10-7.

Структура
Как можно заметить, при малом количестве кругов рекордных значений практически нет. Вероятно, это связано с тем, что при такой размерности критерии остановки алгоритма оказываются слишком грубыми. По получаемому изображению, например, для 5 кругов, видно, что структура составляется верно, но алгоритм не может найти более точно локальный минимум.

Структура
С ростом количества кругов сильно растет влияние фактора случайности генерации центров, поэтому процент рекордных значений уменьшается. При этом программа не редко находит нужную структуру размещения, но ей не удается получить лучшее значение локального минимума.

Заключение
Как показали исследования, при выбранных параметрах алгоритма и критериях сравнения с рекордом количество рекордных значений быстро уменьшается с ростом количества кругов. Чтобы улучшить результаты нужно более детально подобрать значение patience для каждого набора кругов, а также изменять множитель learning rate для более тонкой настройки.
Из приведенных рисунков видно, что во многих случаях программа правильно находит структуру оптимальной упаковки, но не может вычислить значение с высокой точностью.