Содержание
- 2. Информатика – наука об общих свойствах информации, закономерностях и методах её поиска и получения, хранения, передачи,
- 3. Информатика как наука Предметом Информатики как науки являются общие закономерности управления данными, принципы организации и поиска
- 4. Происхождение термина информатика В СССР в 60-е годы – кибернетика. Кибернетика - наука об общих закономерностях
- 5. 1978г. Международный конгресс по информатике Понятие Информатики - охватывает области, связанные с разработкой, созданием, использованием, и
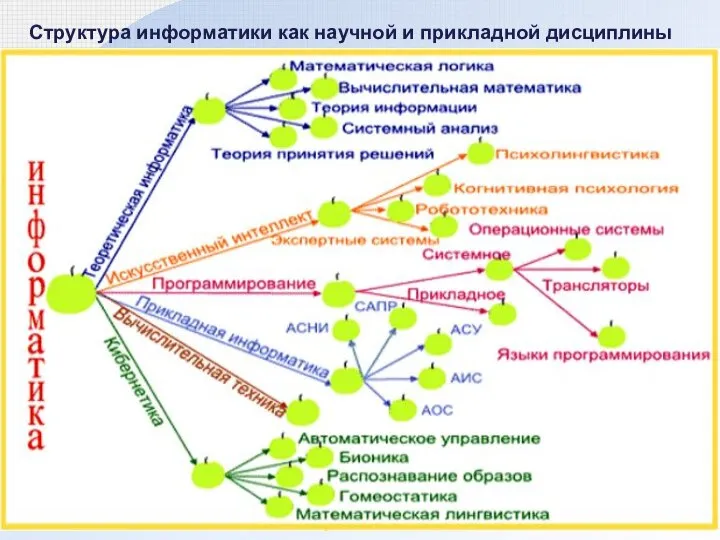
- 6. Структура информатики как научной и прикладной дисциплины
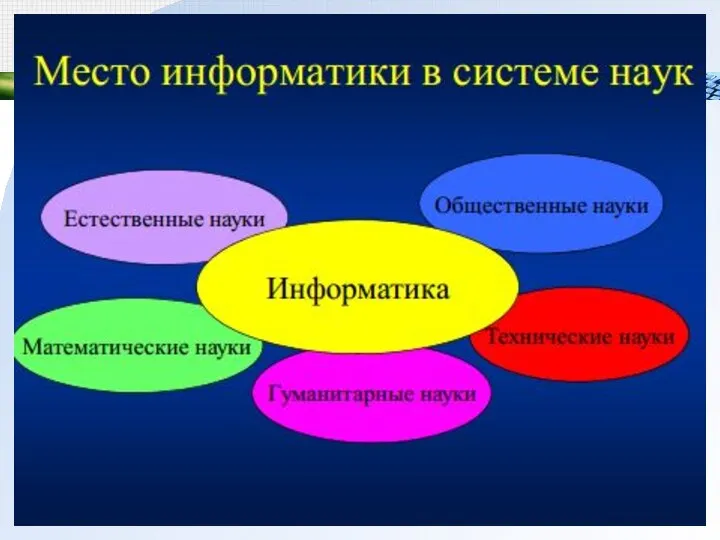
- 8. Естественные науки - имеют дело с объективными сущностями мира, существующими независимо от нашего сознания. Гуманитарные науки
- 9. Информация – сведения и данные, отражающие свойства объектов в природных, социальных и технических системах и передаваемые
- 10. Информация – сведения об объектах и явлениях, их параметрах, свойствах и состоянии, которые уменьшают степень неопределенности
- 11. Цель информатики - поиск нового знания. Информатика - технология обработки накопленного знания и построения нового знания.
- 12. Знание - форма существования и систематизации результатов познавательной деятельности человека. Виды знания: научное, обыденное (здравый смысл),
- 13. Физическая информация: третий компонент материального мира (наряду с веществом и энергией), управляющий порядком и хаосом в
- 14. Смысловая (семантическая) информация: информация, которую воспринимает человек (и которая, к примеру, передаётся средствами массовой информации). Это
- 15. Техническая информация (она же кибернетическая или компьютерная) – информация, передаваемая азбукой Морзе, по радио- или телеканалу,
- 16. Свойства смысловой информации запоминаемость, передаваемость, преобразуемость, воспроизводимость, стираемость, объективность, достоверность, полнота, точность, полезность, ценность, актуальность, понятность,
- 17. Хранение информации Письменность — графическое изображение символов на камне, глине, папирусе, бумаге. Огромное значение в развитии
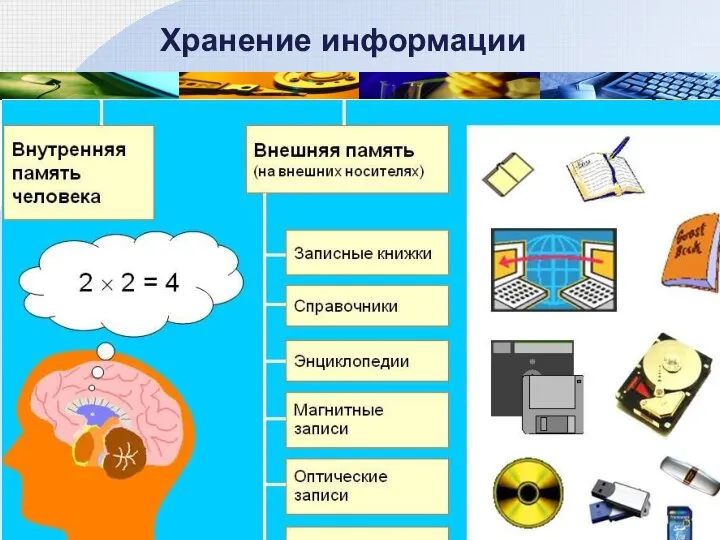
- 18. Хранение информации
- 19. Хранение информации
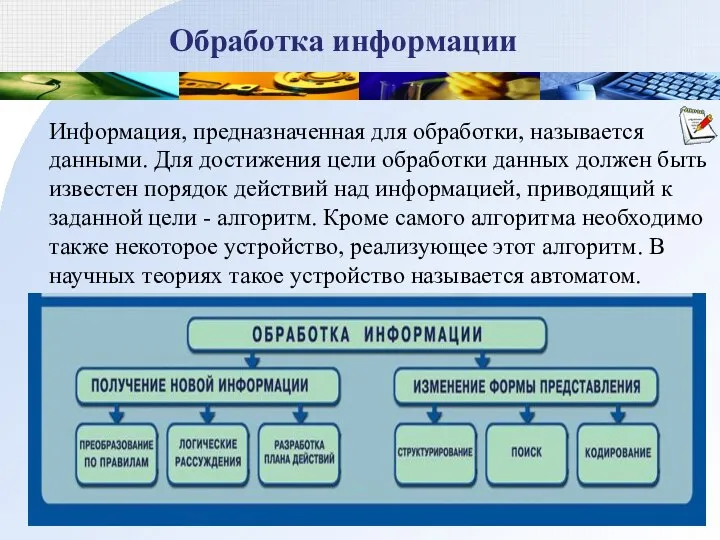
- 20. Обработка информации Информация, предназначенная для обработки, называется данными. Для достижения цели обработки данных должен быть известен
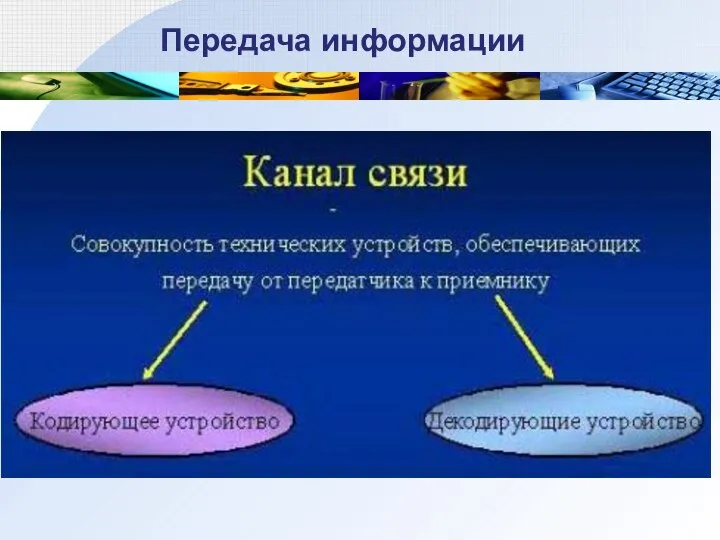
- 21. Передача информации Передачей информации называется процесс её пространственного переноса от источника к получателю. (Речь, письмо и
- 22. Передача информации
- 23. Количество информации
- 24. Меры информации
- 25. Меры информации семантического уровня Тезаурус — совокупность сведений, которыми располагает пользователь или система Зависимость количества семантической
- 26. Меры информации семантического уровня Коэффициент содержательности C - относительная мера семантической информации: C = Ic/Vд, Ic
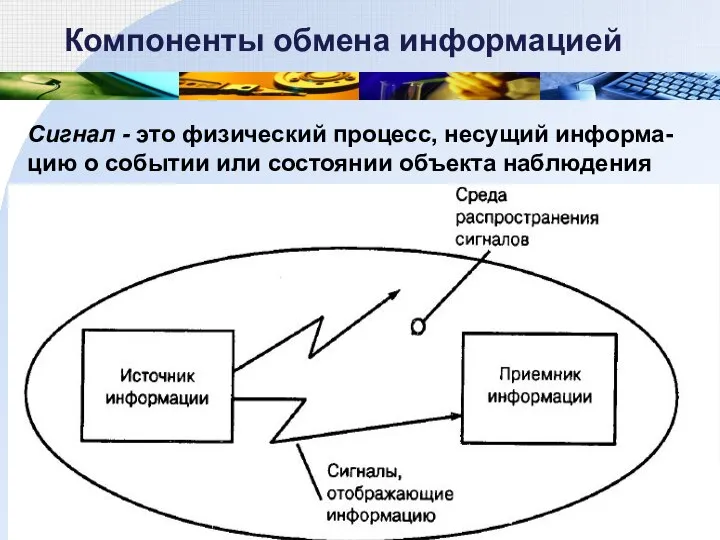
- 27. Компоненты обмена информацией Сигнал - это физический процесс, несущий информа-цию о событии или состоянии объекта наблюдения
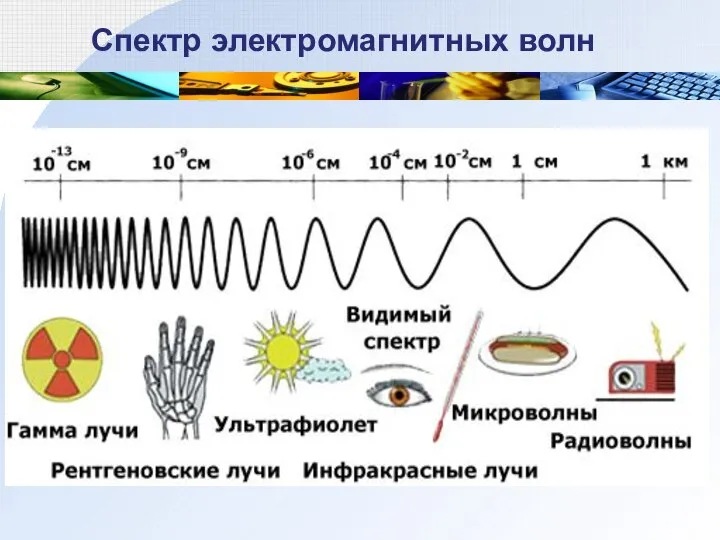
- 28. Спектр электромагнитных волн
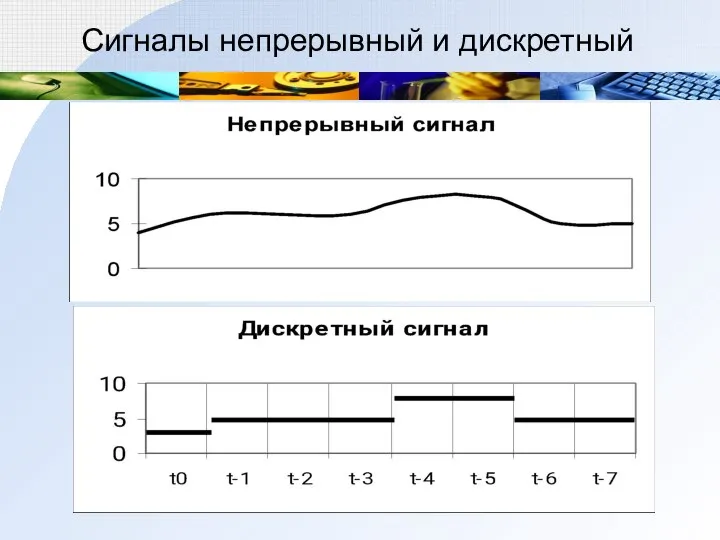
- 29. Сигналы непрерывный и дискретный
- 30. Количество информации, воспринятой приемником, характеризуется не длиной сообщения, а разнообразием сигнала порожденного в приемнике этим сообщением.
- 31. Минимальное разнообразие обеспечивается наличием двух состояний. Информационная ёмкость одной ячейки памяти, способной находиться в двух различных
- 32. Клод Шеннон: «Информация - снятая неопределенность». Неопределенность возникает в ситуации выбора. Задача снятия неопределенности – уменьшение
- 33. Минимальное разнообразие обеспечивается наличием двух состояний. Информационная ёмкость одной ячейки памяти, способной находиться в двух различных
- 34. 1928 г. Р. Хартли: процесс получения информации - выбор одного сообщения из конечного наперёд заданного множества
- 35. Равновероятны ли сообщения "первой выйдет из дверей здания женщина" и "первым выйдет из дверей здания мужчина".
- 36. 1948 г. Клод Шеннон. Формула определения количества информации, учитывающую возможную неодинаковую вероятность сообщений в наборе. Формула
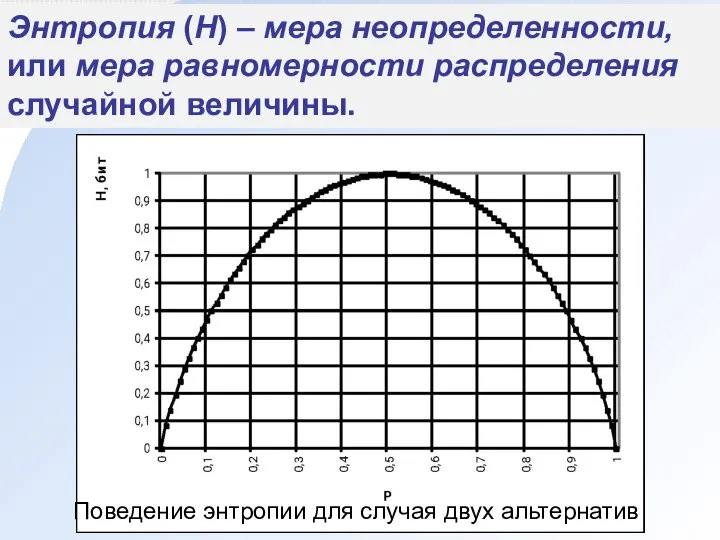
- 37. Энтропия (H) – мера неопределенности, или мера равномерности распределения случайной величины. Поведение энтропии для случая двух
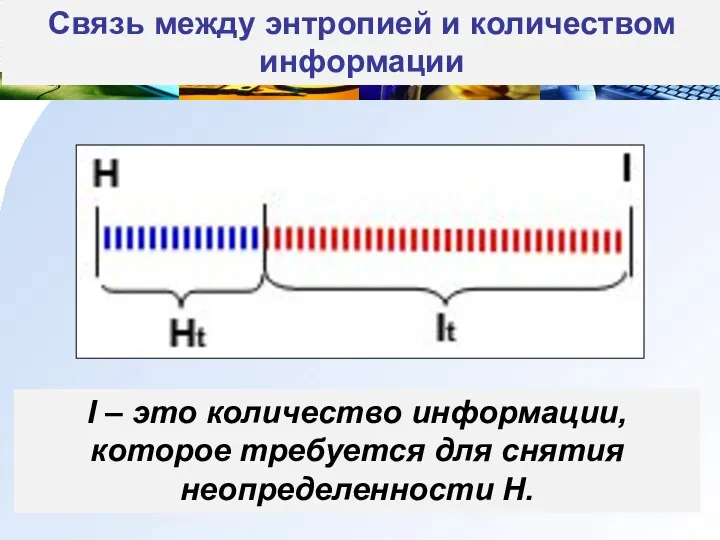
- 38. Связь между энтропией и количеством информации I – это количество информации, которое требуется для снятия неопределенности
- 39. Количество информации в сообщении В общем случае, энтропия H и количество получаемой в результате снятия неопреде-ленности
- 40. Пример. Пусть в некотором учреждении состав работников распределяется так: 3/4 - женщины, 1/4 - мужчины. Тогда
- 41. Количество информации в сообщении Формула Хартли – частный случай формулы Шеннона для равновероятных альтернатив. Подставив в
- 42. Количество информации в сообщении Неопределенность может быть снята только частично, поэтому количество информации I, получаемой из
- 43. Некто вынимает одну карту из колоды (36 карт). Изначальная неопределенность H=log2(36)≅5,17бит. Вытянувший карту сообщает нам часть
- 44. Задача 1. Какое количество информации будет содержать зрительное сообщение о цвете вынутого шарика, если в непрозрачном
- 45. Задача 3. В корзине лежат черные и белые шары. Среди них18 черных шаров. Сообщение о том,
- 46. Решение. Количество символов для кодирования номера составляет: 30 букв + 10 цифр = 40 символов. Количество
- 48. Скачать презентацию


































 Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР
Режимы построения объектов. Использование режимов ОРТО и ПОЛЯР 2._
2._ Курсовая работа. Анализ алгоритмов сортировки массивов. Формат данных для хранения изображения
Курсовая работа. Анализ алгоритмов сортировки массивов. Формат данных для хранения изображения Новостные сообщения по основным новостным каналам
Новостные сообщения по основным новостным каналам Структура сайта. Сайт-визитка
Структура сайта. Сайт-визитка Презентация на тему Основные понятия PowerPoint
Презентация на тему Основные понятия PowerPoint  Примеры построения алгоритмов и их реализации на компьютере
Примеры построения алгоритмов и их реализации на компьютере Что такое информатика? 3 класс
Что такое информатика? 3 класс Информационные технологии
Информационные технологии Язык программирования Smalltalk
Язык программирования Smalltalk Реализация на жесткой и программируемой логике
Реализация на жесткой и программируемой логике Конденсатор в компьютере
Конденсатор в компьютере Анимация. 8-9 класс
Анимация. 8-9 класс Компьютер как универсальное устройство обработки информации
Компьютер как универсальное устройство обработки информации Исходная концептуальная схема обеспечения ИБ
Исходная концептуальная схема обеспечения ИБ Электронная система Охрана труда
Электронная система Охрана труда Мобильное приложение Crazy Color. Проект
Мобильное приложение Crazy Color. Проект Додавання відеокліпів, звукових ефектів і мовного супроводу до слайдової презентації
Додавання відеокліпів, звукових ефектів і мовного супроводу до слайдової презентації Программа Sarafan
Программа Sarafan Функции, рекурсии. Лекция 2
Функции, рекурсии. Лекция 2 Приложение STEmnt. Проект
Приложение STEmnt. Проект Вебинар 12. Предварительно
Вебинар 12. Предварительно 3D – печать. Механизмы и кинематика
3D – печать. Механизмы и кинематика Лонгрид. Мультимедийные элементы
Лонгрид. Мультимедийные элементы Множественные выравнивания
Множественные выравнивания Панель основных процессов (Basic Process)
Панель основных процессов (Basic Process) Семисегментный индикатор
Семисегментный индикатор Обзор составных частей языка
Обзор составных частей языка