Построение таблиц истинности для логических выражений

Вопросы :
Что такое высказывание?
Какие бывают высказывания?
Приведите пример простого высказывания. Сложного высказывания.
Как обозначаются высказывания в Алгебре логики?
Чему могут быть равны логические переменные?

Построение таблиц истинности для логических выражений
Таблица истинности – это таблица, в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения выходной логической функции.

Алгоритм построения таблиц
Определить число переменных
Определить количество строк в таблице истинности
Записать все возможные значения переменных
Определить количество логических операций и их порядок
Записать логические операции в таблицу истинности
Определить для каждой операции значение.

Определение количества строк в таблице.
Где N – количество строк в таблице
q – количество логических переменных, участвующих в данном высказывании.

Порядок выполнения действий
Инверсия (отрицание)
Операции в скобках
Конъюнкция (логическое умножение)
Дизъюнкция (логическое сложение)
Импликация (следование)
Эквиваленция (равенство)

Построение таблиц истинности для логических выражений
Постройте таблицу истинности для следующего логического выражения:
F(A,B,C)= ¬(A&B˅¬C)
Где F – это логическое высказывание(логическая функция).
В скобках пишут от каких логических переменных зависит высказывание( в нашем случае от трёх переменных:A,B,C).

Построение таблиц истинности для логических выражений.

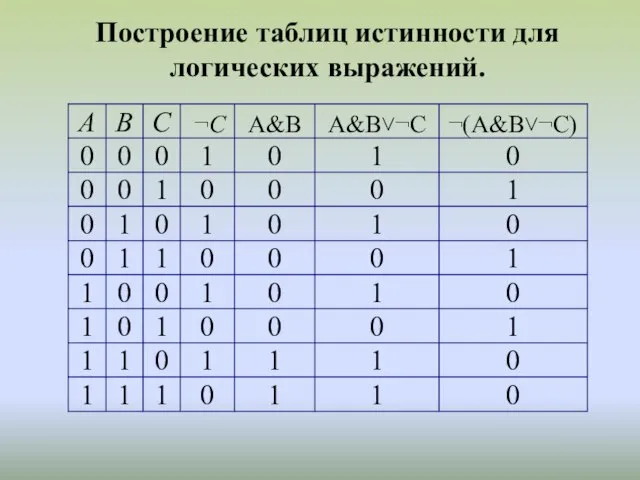
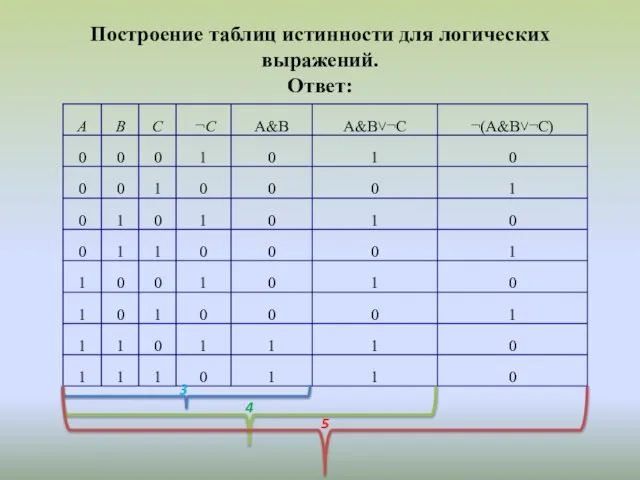
Построение таблиц истинности для логических выражений.
Ответ:
3
4
5

Пример 2:
Построить таблицу истинности(ТИ) для следующей логической функции:
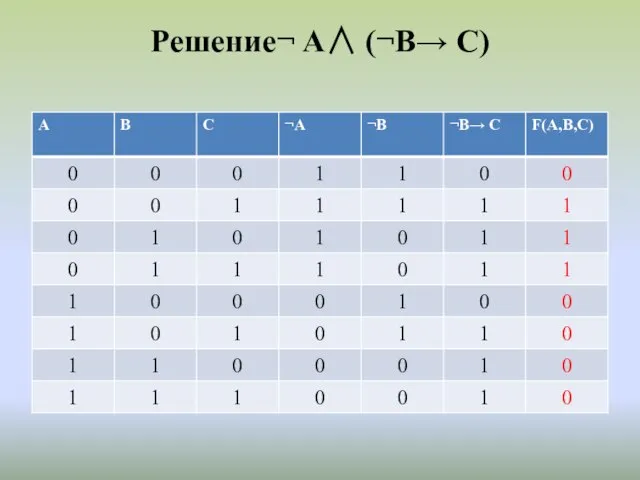
F(A,B,C)=(А∧ ¬В)→ ¬С

Решение

Пример 3:
Построить таблицу истинности(ТИ) для следующей логической функции:
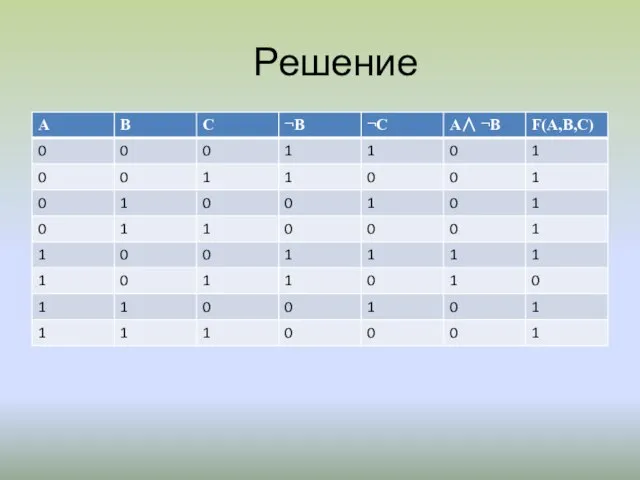
F(A,B,C)= ¬ А∧ (¬В→ С)

Решение¬ А∧ (¬В→ С)

Домашняя работа
Составьте таблицы истинности:
F(A,B,C)= ¬((А∨В)→С)
F(A,B,C)= ¬(А∨В∧¬С)
F(A,B,C)= (А∧ В) ∨ ¬ (С∧ В)
F(A,B,C)=(А∨¬В)→(¬С∧¬А)
F(X,Y,Z)=(¬X ∧ ¬Z∨Y) ↔ ¬(Z ∧ Y) →(X∨¬Y)