Позиционные системы счисления

Содержание
Определения
Непозиционные системы счисления
Римская система счисления
Правила перевода из риской системы счисления в десятичную
Позиционные системы
Примеры позиционных систем
Двоичная система счисления
Перевод из десятичной системы счисления в двоичную
Перевод из двоичной системы счисления в десятичную
Восьмеричная система счисления
Перевод из двоичной системы счисления в восьмеричную
Шестнадцатеричная система счисления
Перевод из двоичной системы счисления в шестнадцатеричную
Задачи и упражнения
Заключение
Ответы к упражнениям
Список литературы

Определения
Система счисления – набор правил представления и наименования чисел.
Цифры – знаки, используемые для записи чисел.
Числа: 256, 12, 100101, CXL.
Пример: десятичная система счисления, римская система счисления.

Непозиционные системы счисления
Унарная система счисления: одна цифра обозначает единицу (1 час, 1 день, 1 монета, 1 верблюд и т.п.). Человек догадался, что для счета можно использовать все, что попадется под руку.
Древнеегипетская система счисления: использовались специальные цифры для обозначения чисел.
Пример №1. Число 3215:

Римская система счисления
Римляне обозначали числа специальными символами (буквами). Натуральные числа записываются при помощи повторения этих цифр. Например, II = 1+1 =2, где I обозначает единицу, независимо от её места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Часы куранты Спасской башни Московского кремля с римскими цифрами на циферблате

Правила перевода из римской системы счисления в десятичную
Больше трех одинаковых цифр подряд не ставят.
Если младшая цифра (только одна) стоит слева от старшей, то она вычитается из суммы
Если младшие цифры (одна или две) стоят справа от старшей, то они суммируются.

Позиционные системы
В позиционных системах счисления значение цифры определяется ее позицией в записи числа.
Разряд – положение цифры в форме записи числа.
Десятичная система счисления – позиционная система по основанию 10.
Алфавит: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}

Примеры позиционных систем
Пятеричная: счетным «прибором» служат пальцы рук.
Двенадцатеричная: возникла в древнем Шумере, вероятно для подсчета использовались фаланги на руке большим пальцем. Сохранившиеся способы применения:
год состоит из 12 месяцев;
половина суток состоит из 12 часов;
дюжина содержит 12 единиц;
в британской системе мер 1 фут равен 12 дюймов;
английский фунт состоит из 12 шиллингов, 1 шиллинг из 12 пенсов.
Двадцатеричная: используется во многих языках (азиатских и кавказских), в системе записи чисел майя и ацтеков.
Шестидесятеричная: придумана в Древнем Вавилоне, в ней использовалось шестьдесят цифр.

Двоичная система счисления
Для компьютера эффективна система двоичных чисел, основанная только на двух цифрах – 0 и 1.
Двоичная система идеальна для компьютера, поскольку во время работы используется электрический ток: он либо течет по цепи (цепь включена), либо не течет (цепь выключена).
В компьютере двоичные числа 0 и 1 можно использовать для описания электрических сигналов по принципу включено-выключено. На этом простом принципе основана работа центрального процессора.
Все входные данные преобразуются в нули и единицы, при этом нуль означает отсутствие тока в цепи (т.е. выключение цепи), единица – присутствие тока в цепи (т.е. включение цепи).
Два числа – 0 и 1 – называют битами. Слово «bit» (бит) представляет собой сокращенную форму термина binary digit (двоичный разряд). Бит – это 0 или 1.
Недостаток двоичного кодирования – длинные коды. Но в технике проще обрабатывать большое количество простых элементов, чем небольшое число сложных.

Двоичная система счисления
Используется для представления числовых данных в компьютерах и других электронных вычислительных устройствах.
Алфавит: {0, 1}
Основание (количество цифр): 2
1·27+ 0·26+ 1·25+ 0·24+ 0·23+ 1·22+ 1·21+ 0·20=128 + 32 + 4 + 2 = 166

Необыкновенная девочка (А.Н. Стариков)
Ей было тысяча сто лет,
Она в 101-ый класс ходила,
В портфеле по сто книг носила –
Все это правда, а не бред.
Когда, пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять темно-синих глаз
Рассматривали мир привычно,…
Но станет все совсем обычным,
Когда поймете наш рассказ.

Перевод из десятичной системы счисления в двоичную
Число делится на 2, после чего запоминается остаток от деления. Полученное частное вновь делится на 2, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на 2 выписываются в порядке, обратном их получению.
Пример №2. Перевести число 860 из десятичной системы счисления в двоичную.
86(10) =1010110(2)
Пример №3. Перевести число 149 из десятичной системы счисления в двоичную. 149(10) =10010101(2)

Метод подбора
Определяем наибольшую степень 2, которая меньше данного числа. Например, для числа 89, это 64 = 26.
Вычитаем эту степень из исходного числа: 89 – 64 = 25.
Повторяем для полученной разности с п.1, пока не получим 0.
Пример №4. 89 = 64 + 25 = (64 + 16) + 9 = (64 + 16 + 8) + 1 = 1·26 + 0·25 +1·24 + 1·23 + 0·22 + 0·21 +1· 20
89(10) = 1011001(2).

Упражнение №1
Переведите в двоичную систему счисления следующие числа:
167
205
47
81

Перевод из двоичной системы счисления в десятичную
При переводе чисел из двоичной системы счисления в десятичную необходимо пронумеровать разряды справа налево, начиная с нуля. Затем вычислить сумму соответствующих значений разрядов, помноженных на основания системы счисления в степени, равной номеру разряда. В результате получим представление исходного числа в десятичной системе счисления.
Пример №5. Перевести числа из двоичной системы счисления в десятичную.
1111000(2) = 1⋅26 + 1⋅25 + 1⋅24 +1⋅23 + 0⋅22 + 0⋅21 +0⋅20 =131(10)
100111100(2) = 1⋅28 + 1⋅25 + 1⋅24 + 1⋅23 + 1⋅22 = 316(10)

Упражнение №2
Переведите из двоичной системы счисления в десятичную следующие числа:
101101;
1101101;
1111;
1010110.

Восьмеричная система счисления
Пример №6. Перевести число 154 из десятичной системы счисления в восьмеричную: 154(10) = 232(8);
Пример №7. Перевести число 276 из восьмеричной системы счисления в десятичную:
276(8) = 2·82 + 7 · 81 + 6 · 80 = 2 · 64 + 7 · 8 + 6 = 190(10)
Основание (количество цифр): 8
Алфавит: {0, 1, 2, 3, 4, 5, 6, 7}
Перевод из десятичной системы в восьмеричную: Число делится на 8, после чего запоминается остаток от деления. Полученное частное вновь делится на 8, остаток запоминается. Процедура продолжается до тех пор, пока частное станет меньше 8. Это частное становится первой цифрой. Далее выписываются остатки от деления в порядке, обратном их получению.

Таблица чисел в двоичной и восьмеричной системах счисления

Перевод из двоичной системы счисления в восьмеричную
Перевести из двоичной системы счисления в восьмеричную и наоборот очень просто!
Налево от младшего разряда откладываем триады – группы по три цифры. После этого записываем из в восьмеричном виде.
Неполные триады дополняем нулями слева.
Пример №8. Перевести из двоичной системы в восьмеричную 1101110011(2) = 1563(8)
Пример №9. Перевести из восьмеричной системы в двоичную 3512(8) = 11101001010(2)

Шестнадцатеричная система счисления
Основание (количество цифр): 16
Алфавит: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}
Перевод из десятичной системы в шестнадатеричную: Число делится на 16, после чего запоминается остаток от деления. Полученное частное вновь делится на 16, остаток запоминается. Процедура продолжается до тех пор, пока частное станет меньше 16. Это частное становится первой цифрой. Далее выписываются остатки от деления в порядке, обратном их получению.
Пример №10. Перевести число 155 из десятичной системы счисления в шестнадцатеричную:
155(10) = 9B(16);
Пример №11. Перевести число 1DA из шестнадцатеричной системы счисления в десятичную:
1DA(16) = 1·162 + 13 · 81 + 10 · 80 = 1 · 256 + 13 · 8 + 10 = 370(10)

Таблица чисел в двоичной и шестнадцатеричной системах счисления

Перевод из двоичной системы счисления в шестнадцатеричную
Перевести из двоичной системы в шестнадцатеричную и наоборот очень просто!
Налево от младшего разряда откладывает тетрады – группы по четыре цифры. После этого записываем из в шестнадцатеричном виде.
Неполные тетрады дополняем нулями слева.
Пример №12. Перевести из двоичной системы в шестнадцатеричную 1011100101(2) = 2E5(16)
Пример №13. Перевести из шестнадцатеричной системы в двоичную AB2(16) = 101010110010(2)

Задача №1
Число 437 записали в системах счисления с основаниями от 2 до 10 включительно. При каких основаниях сумма цифр этого числа является простым числом? В ответе укажите сумму всех подходящих оснований.

Решение
Переведем число 437 в системы счисления, основания которых являются степенями двойки: 2, 4, 8.
Для перевода числа в двоичную систему счисления делим последовательно число 437 на 2. Получаем: 437(10) = 110110101(2). Сумма цифр числа = 6, не является простым числом.
Для перевода числа в систему счисления с основанием 4, воспользуемся двоичным числом, разбив его на пары цифр. Каждую пару преобразуем в четверичные цифры. Получим: 437(10) = 12311(4). Сумма цифр числа = 8, не является простым числом.
Для перевода числа в систему счисления с основанием 8, также воспользуемся двоичным числом, разбив его на триады цифр. Каждую тройку цифр преобразуем в восьмеричные цифры. Получаем: 437(10) = 665(8). Сумма цифр числа = 17, это простое число.
Перевод десятичного числа в двоичную систему счисления
Перевод двоичного числа в четверичную систему счисления
Перевод двоичного числа в восьмеричную систему счисления

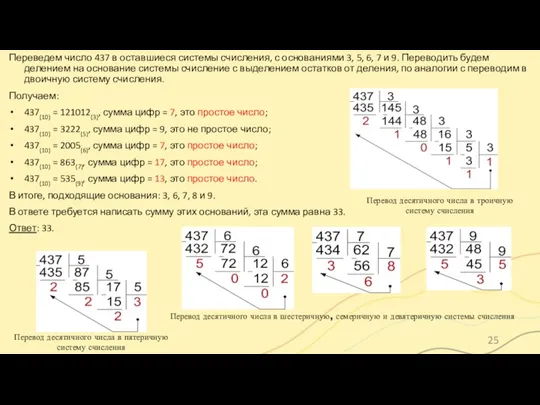
Переведем число 437 в оставшиеся системы счисления, с основаниями 3, 5, 6, 7 и 9. Переводить будем делением на основание системы счисление с выделением остатков от деления, по аналогии с переводим в двоичную систему счисления.
Получаем:
437(10) = 121012(3), сумма цифр = 7, это простое число;
437(10) = 3222(5), сумма цифр = 9, это не простое число;
437(10) = 2005(6), сумма цифр = 7, это простое число;
437(10) = 863(7), сумма цифр = 17, это простое число;
437(10) = 535(9), сумма цифр = 13, это простое число.
В итоге, подходящие основания: 3, 6, 7, 8 и 9.
В ответе требуется написать сумму этих оснований, эта сумма равна 33.
Ответ: 33.
Перевод десятичного числа в троичную систему счисления
Перевод десятичного числа в пятеричную систему счисления
Перевод десятичного числа в шестеричную, семеричную и девятеричную системы счисления

Упражнение №3
Число 210 записали в системах счисления с основаниями от 2 до 10 включительно. При каких основаниях цифры этого числа при чтении слева направо образуют убывающие арифметические прогрессии? В ответе укажите сумму всех подходящих оснований.

Задача №2
В какой системе счисления выполняется равенство 12X · 13X = 211 X? В ответе укажите число – основание системы счисления.

Решение
Рассмотрим уравнение 12X · 13X = 211 X, переведем все числа в десятичную систему счисления:
12x =1 ·x+2; 13x = 1 ·x+3;
211x = 2 ·x2+1 ·x+1.
Перепишем уравнение в десятичной системе счисления:
(x+2) ·(x+3) = 2 ·x2+x+1.
Раскроем скобки и приведем подобные члены, получим квадратное уравнение:
x2 – 4x – 5 =0,
корни которого x1 = -1 и x2 = 5.
Проверка: 12(5) = 1 ·5+2 = 7, 13(5) = 1 ·5+3=8, 211(5) = 2 ·52+1 ·5+1 = 56;
7 ·8 = 56 – верное тождество.
Ответ: 5.

Упражнение №4
В каких системах счисления выполняются равенства:
21X · 13X = 313 X
12X · 31X = 402 X
13X · 31X = 423 X
12X · 33X = 406 X

Задача №3
Решите уравнение 42(5) + x(10) = 1122(3).
Решение:
Переведем в десятичную систему счисления каждое слагаемое уравнения:
42(5) = 4⸱51 + 2=22(10);
1122(3) = 1 ⸱33 + 1 ⸱32 + 2 ⸱31 + 2 = 27 + 9 + 6 + 2 = 44.
Получим уравнение в десятичной системе:
22 + x = 44.
Корень уравнения: x = 22.
Ответ: 22.

Упражнение №5
Решите уравнения:
100(7) + x(10) = 230(5);
54(7) + x(10) = 320(5);
32(8) + x(10) = 214(5).

Задача №4
Решите уравнение 101(x) + 13(10) = 101(x+1).
Решение:
Переведем каждый член уравнения в десятичную систему счисления:
101x = 1⸱x2 + 0 ⸱x1 + 1 ⸱x0 = x2 + x;
101(x+1) = 1 ⸱(x+1)2 + 0 ⸱(x+1)1 + 1 ⸱(x+1)0 = x2+ 2x + 2;
Получим следующее уравнение: x2 + 14 = x2 + 2x + 2.
После приведения подобных получаем линейное уравнение 2x = 12, корень которого x = 6.
Выполним проверку:
101(6) = 1 ⸱62 + 0 ⸱61 + 1 ⸱60 = 36 + 1 =37(10);
101(7) = 1⸱72 + 0 ⸱71 + 1⸱70 = 49 + 1 = 50(10);
37 + 13 = 50 – верное тождество.
Ответ: 6

Упражнение №6
Решите уравнения:
103(x) + 11(10) = 103(x+1);
104(x) + 20(x) = 84(10).

Задача №5
Найти основания систем счисления x и y:
87x = 73y;
62x = 52y.
Решение:
Приведем все части уравнений в десятичную систему счисления, получим следующую систему уравнений относительно неизвестных x и y:
8⸱x + 7 = 7 ⸱y + 3
6 ⸱x + 2 = 5 ⸱y + 2
После преобразования:
8⸱x - 7 ⸱y = -4;
6 ⸱x - 5 ⸱y = 0.
Решение уравнения: x = 10, y = 12.
Проверка:
87(10) = 73(12) → 87 = 7 ⸱12 + 3 – верное тождество.
62(10) = 52(12) → 62 = 5 ⸱12 + 2 – верное тождество.
Ответ: x = 10, y = 12.

Заключение
Двоичные числа имеют много разрядов, человеку сложно оперировать с ними, но для компьютера намного проще выполнение операций с двоичными числами, чем с десятичными.
Двоичные коды обладают надежностью и помехоустойчивостью. Для работы с ними нужны устройства только с двумя устойчивыми состояниями (есть ток – нет тока).
Двоичная система используется практически во всех современных компьютерах и вычислительных электронных устройствах.
Восьмеричная система широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами.

Ответы к упражнениям

Упражнение №1
Переведите в двоичную систему счисления следующие числа:
167(10) = 10100111(2);
205(10) = 11001101(2);
47(10) = 101111(2);
81(10) = 1010001(2).

Упражнение №2
Переведите из двоичной системы счисления в десятичную следующие числа:
101101(2) = 1⸱25+1 ⸱ 23+1 ⸱ 22+1 ⸱ 20 = 45(10);
1101101(2) = 1⸱26+1 ⸱ 25+1 ⸱ 23+1 ⸱ 22+1 ⸱ 20 = 109(10);
1111(2) = 1 ⸱ 23+1 ⸱ 22+1 ⸱ 21+1 ⸱ 20 = 15(10);
1010110(2) = 1 ⸱ 26+1 ⸱ 24+1 ⸱ 22+1 ⸱ 21= 86(10).

Упражнение №3
Число 210 переведем в системы счисления с основаниями от 2 до 10. Цифры исходного числа 210 образуют убывающую арифметическую прогрессию с шагом 1.
210(10) = 11010010(2);
210(10) = 21210(3);
210(10) = 3102(4);
210(10) = 1320(5);
210(10) = 550(6);
210(10) = 420(7); цифры 4, 2 и 0 образуют убывающую арифметическую прогрессию с шагом 2.
210(10) = 322(8);
210(10) = 253(9).
Ответ: подходящие основания: 10 и 7, их сумма равна 17.

Упражнение №4
Основания систем счисления:
x = 6;
x = 7;
x = 8;
x = 9.

Упражнение №5
Решите уравнения:
100(7) + x = 230(5) →49 + x = 65 → x = 16
54(7) + x = 320(5) → 39 + x = 85 → x = 46
32(8) + x = 214(5) → 26 + x = 59 → x = 33

Упражнение №6
Решение уравнений:
Ответ: 5.
Ответ: 8.