Содержание
- 2. Система счисления - это правило записи чисел с помощью заданного набора специальных знаков - цифр.
- 3. Позиционными - значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.
- 4. Пусть р - основание системы счисления. Тогда любое число Z, удовлетворяющее условию Z
- 5. aj - целые числа, удовлетворяющие условию: значение р = 2 - является минимальным для позиционных систем.
- 6. 4.2. Представление чисел в различных системах счисления 4.2.1. Перевод целых чисел из одной системы счисления в
- 7. Преобразование Zp → Z1 → Zq Пусть Zq= 0; из числа Zp вычтем 1 по правилам
- 8. Пример 4.1 Выполнить 223 → Z6. 223 = 126.
- 9. Преобразование Zp → Z10 → Zq Z10 → Zq целочисленно разделить исходное число (Z10) на основание
- 10. Zp → Z10 Необходимо Zp представить в форме многочлена и выполнить все операции по правилам десятичной
- 11. 4.2.2. Перевод дробных чисел из одной системы счисления в другую Правильную дробь в исходной системе счисления
- 12. 0, Yp → 0,Y10 → 0,Yq Перевода 0,Y10 → 0,Yq умножить исходную дробь в 10-ной системе
- 13. Пример 4.4. Выполнить преобразование 0,37510 → 0,Y2 Таким образом, 0,37510 = 0,0112.
- 14. Перевод 0,Yp → 0,Y10, Сводится к вычислению значения многочлена в десятичной системе счисления.
- 15. Пример 4.5 Выполнить преобразование 5,3(3)10 → Х3. Ответ: 5,3(3)10 = 12,13.
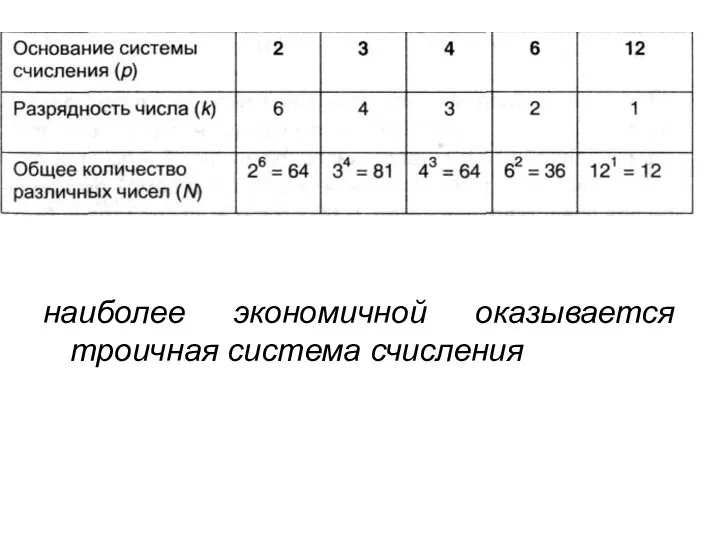
- 16. 4.2.3. Понятие экономичности системы счисления Число в системе счисления р с k разрядами, будет иметь наибольшее
- 17. Количество разрядов числа при переходе от одной системы счисления к другой в общем случае меняется. Если
- 18. Сравним количество цифр в числе 9910 и его представлении в двоичной системе счисления: 9910 = 11000112;
- 19. Экономичность системы счисления -количество чисел, которое можно записать в данной системе с помощью определенного количества цифр.
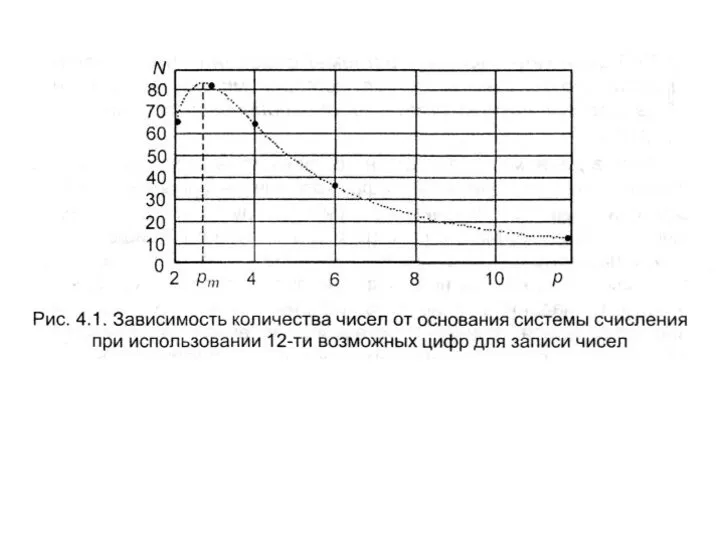
- 20. наиболее экономичной оказывается троичная система счисления
- 21. Пусть имеется n знаков для записи чисел, р - основание системы счисления. Количество разрядов числа k
- 23. получаем ln p = 1, или р = е, е = 2,71828.. Ближайшее к е целое
- 24. 4.2.4. Преобразование нормализованных чисел Вещественное число X может быть представлено в двух формах - естественной и
- 25. М10 - мантисса нормализованного числа. Значения мантиссы лежат в интервале 0,1 ≤ М10 ≤ 1; k
- 26. Примеры: -123410 = -0,1234∙104 0,0345610 = 0,3456∙10-1. !!!! Нормальное представления числа, мантисса лежит в интервале 1
- 27. Нормализованная форма числа в произвольной системе счисления р: р-1 ≤ Мр Для р = 2:
- 28. В компьютере все вещественные числа хранятся и обрабатываются в нормализованном двоичном представлении при их вводе осуществляется
- 29. Пример 4.8 16,510 → X2. Отдельно целую и дробную части 1610 = 100002, 0,510 = 0,12
- 30. Пример 4.9 (0,11∙2110)2 → Х10 0,112 = 0,7510 (2110)2 = (26)10 = 64 (0,11∙2110)2 = 0,75∙64
- 31. 4.3. Кодирование чисел в компьютере и действия над ними 4.3.1. Кодирование и обработка в компьютере целых
- 32. Для записи числа выделяется фиксированное количество двоичных разрядов. Память компьютера имеет байтовую структуру. Размер одной адресуемой
- 33. Пусть количество разрядов k и p = 2 тогда, (Z2)max = 2k - 1. при k
- 34. Число 65636 и более в компьютере не может существовать!!! Минимальным целым числом в беззнаковом представлении, является
- 35. В языке программирования PASCAL целые числа без знака, для записи которых отводится 2 байта, определены как
- 36. Выход за границу 65535 возможен только путем увеличения количества разрядов для записи числа. Необходим новый тип
- 37. 4.3.2. Кодирование и обработка в компьютере целых чисел со знаком 1. Прямой код. Один (старший) разряд
- 38. Остается 15 двоичных разрядов, что обеспечивает наибольшее значение числа Zmax = 215 - 1 = 3276710.
- 39. Пример 4.10 159410 + 1756310 при беззнаковой двоичной кодировке и 16-битном машинном слове.
- 40. Пример 4.11 – переполнение типа! Найти сумму 6553410 + 310
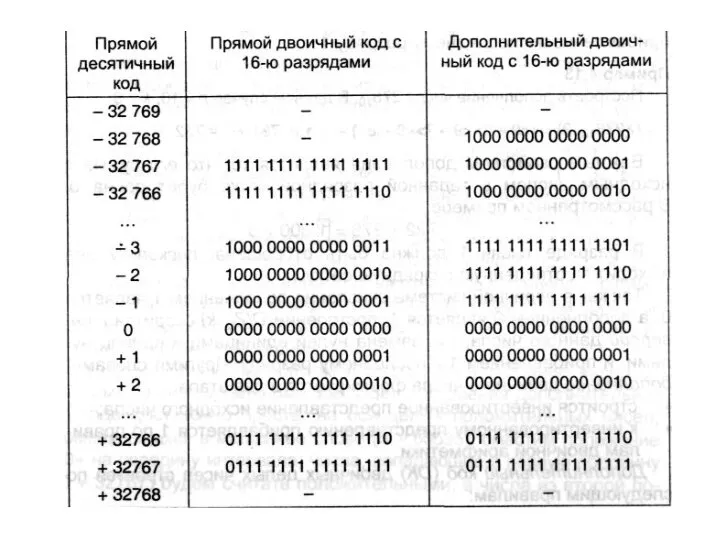
- 41. 2. Дополнительный код Ось целых положительных чисел, (0 ÷ 65535), сместим положение «О» на середину, числа,
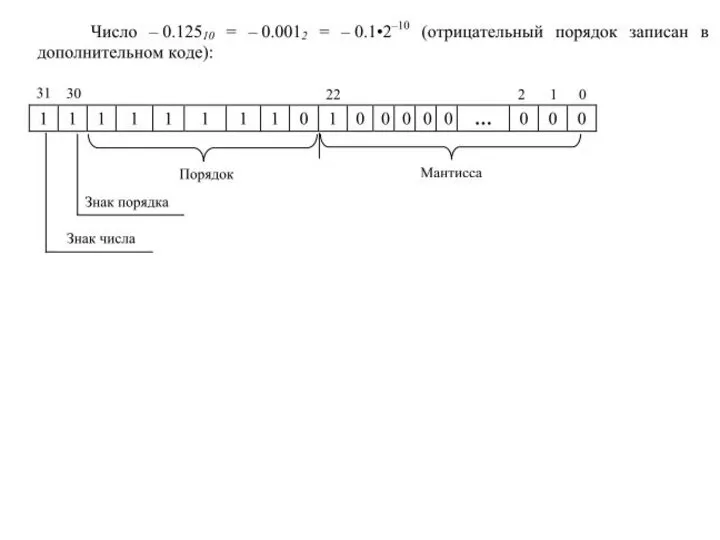
- 42. Пример 1000000000000012 = 3276910 – код отрицательного числа. 0000000000000012 = 110 - код положительного числа. Старший
- 43. Способ построения дополнительного кода целых чисел Дополнением (D) k-разрядного целого числа Z в системе счисления р
- 44. Дополнительный код (DK) двоичных целых чисел строится по следующим правилам: для положительных Z2 ≥ 0 дополнительный
- 45. Пример 4.14 Построить дополнительные двоичные коды чисел (а) 310 и (b) -310.
- 47. в 2-байтном машинном слове интервал чисел [-32768; 32767] - типа Integer в языке PASCAL. Перевод в
- 48. Операция вычитания двух чисел как самостоятельная отсутствует - она заменяется сложением первого числа с дополнительным кодом
- 49. При выполнении вычитания отрицательного числа оно из дополнительного кода переводится в прямой, и вновь вместо вычитания
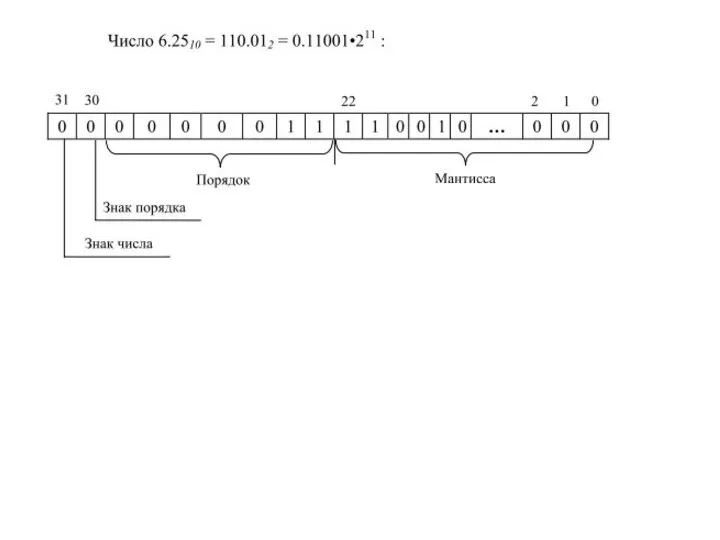
- 50. Основная форма представления кодов вещественных чисел - двоичная нормализованная. Записываются и хранятся в памяти все составляющие
- 51. Поскольку значение мантиссы лежит в интервале 0,1 Первая цифра мантиссы также не сохраняется (она для всех
- 52. Пример. Количество цифр в числе 99 и его представлении в двоичной системе счисления 99 = 1100011
- 54. В процессе выполнения арифметических действий с нормализованными числами отдельно обрабатываются мантиссы и порядки. Сложение нормализованных чисел
- 59. Выполнить вычитание двоичных нормализованных чисел 0.10101 . 210 и 0.11101 . 21. Разность порядков уменьшаемого и
- 60. Выполнить умножение двоичных нормализованных чисел: (0.11101 . 2101) . (0.1001 . 211) (0.11101 . 0.1001) .
- 64. Скачать презентацию










































![в 2-байтном машинном слове интервал чисел [-32768; 32767] - типа Integer в](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1070243/slide-46.jpg)













 Web-программирование. Лекция 5. Шаблоны проектирования
Web-программирование. Лекция 5. Шаблоны проектирования Правила работы и безопасного поведения в компьютерном классе
Правила работы и безопасного поведения в компьютерном классе Использование облачных технологий в деятельности педагога
Использование облачных технологий в деятельности педагога Известия VS Медиазона
Известия VS Медиазона Аудит divine-light.ru_версия 21092022
Аудит divine-light.ru_версия 21092022 Основы музейных коммуникаций
Основы музейных коммуникаций Internet Protocol (IP)
Internet Protocol (IP) ВКонтакте - российская социальная сеть
ВКонтакте - российская социальная сеть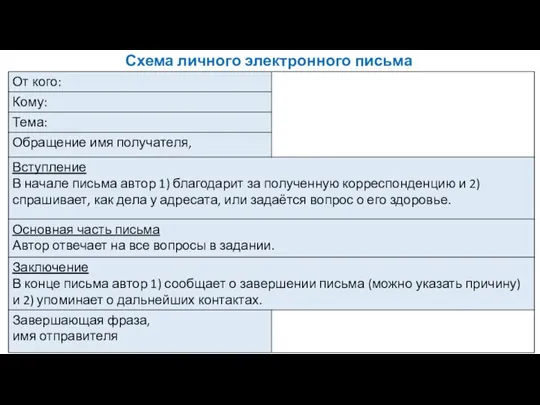 Схема личного электронного письма
Схема личного электронного письма Мобильное электронное образование в детских садах и дома
Мобильное электронное образование в детских садах и дома Базовые показатели эффективности (БПЭ)
Базовые показатели эффективности (БПЭ) Представление звуковой информации
Представление звуковой информации Технология промышленного производства
Технология промышленного производства Сеть для организаций. Отчет о проектной работе
Сеть для организаций. Отчет о проектной работе Умные таблицы Excel 2007-2013
Умные таблицы Excel 2007-2013 Строки как одномерные массивы данных типа char (терминальные строки)
Строки как одномерные массивы данных типа char (терминальные строки) Азбука журналистики
Азбука журналистики Краудсорсинг в ИТ рекрутменте
Краудсорсинг в ИТ рекрутменте Метрология и теория измерений
Метрология и теория измерений одирование тестовой, графической и звуковой информации
одирование тестовой, графической и звуковой информации Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3)
Вводное занятие. Система отслеживания багов и задач JIRA (лекция - 3) Инструкция по входу в ZOOM
Инструкция по входу в ZOOM Das At-Zeichen
Das At-Zeichen Презентация на тему Поколение ЭВМ
Презентация на тему Поколение ЭВМ  Понятие информация
Понятие информация Web - страницы. Язык HTML
Web - страницы. Язык HTML Ресурсы для защиты информации в веке IT технологий
Ресурсы для защиты информации в веке IT технологий Одномерные массивы целых чисел. Описание, заполнение, вывод массива
Одномерные массивы целых чисел. Описание, заполнение, вывод массива