Содержание
- 2. Равномерный закон распределения
- 4. Сфера применения равномерного закона распределения
- 5. Определение. Непрерывная случайная величина Х распределена по показательному закону с параметром λ, если плотность вероятности ее
- 6. Доказательство
- 7. Сфера применения показательного закона распределения В сфере массового обслуживания, с простейшим потоком событий, время обслуживания заявки
- 8. Нормальный закон распределения
- 9. Свойства нормального закона распределения:
- 10. Пример (задача 4.21. Кремер). Коробки с конфетами упаковываются автоматически. Их средняя масса равна 540 г. Известно,
- 11. а) б) в) г)
- 12. Логарифмически-нормальное распределение
- 14. Логонормальное распределение используется для описания распределения доходов, банковских вкладов, цен активов, месячной заработной платы, посевных площадей
- 16. Скачать презентацию













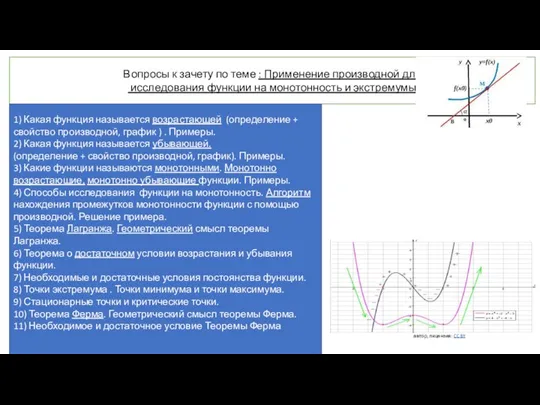 Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Упрощение выражений. Урок с использованием ИКТ
Упрощение выражений. Урок с использованием ИКТ Основы теории оболочек вращения
Основы теории оболочек вращения Презентация на тему Основные тригонометрические формулы
Презентация на тему Основные тригонометрические формулы  Симметрия. Виды симметрии
Симметрия. Виды симметрии Смешанные числа (часть 2)
Смешанные числа (часть 2) Эвристические приемы. Алгебра 8 класс
Эвристические приемы. Алгебра 8 класс Памятки по математике
Памятки по математике Инфекционные заболевания с кожным симптомом
Инфекционные заболевания с кожным симптомом Решение задач на перебор вариантов
Решение задач на перебор вариантов Презентация на тему Построение треугольника по трем элементам
Презентация на тему Построение треугольника по трем элементам  Относительные показатели: динамики, плана, координации
Относительные показатели: динамики, плана, координации Основные законы теории вероятности
Основные законы теории вероятности Примеры на 5
Примеры на 5 Презентация на тему Прогрессии
Презентация на тему Прогрессии  Состав чисел в приделах 10. Решение задач
Состав чисел в приделах 10. Решение задач Степень с натуральным показателем. Обобщающий урок в 7 классе
Степень с натуральным показателем. Обобщающий урок в 7 классе Теория статистики. Предмет, задачи, основные категории и понятия статистики
Теория статистики. Предмет, задачи, основные категории и понятия статистики Презентация на тему Измерения без линейки
Презентация на тему Измерения без линейки  Сумма бесконечной геометрической прогрессии
Сумма бесконечной геометрической прогрессии Презентация на тему Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов
Презентация на тему Методические особенности обучения учащихся решению уравнений в курсе математики 5-7 классов  Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Схемы и типы задач. Путешествие в сказку
Схемы и типы задач. Путешествие в сказку Комбинаторные задачи
Комбинаторные задачи Определение арктангенса и арккотангенса числа а
Определение арктангенса и арккотангенса числа а Построение сечений
Построение сечений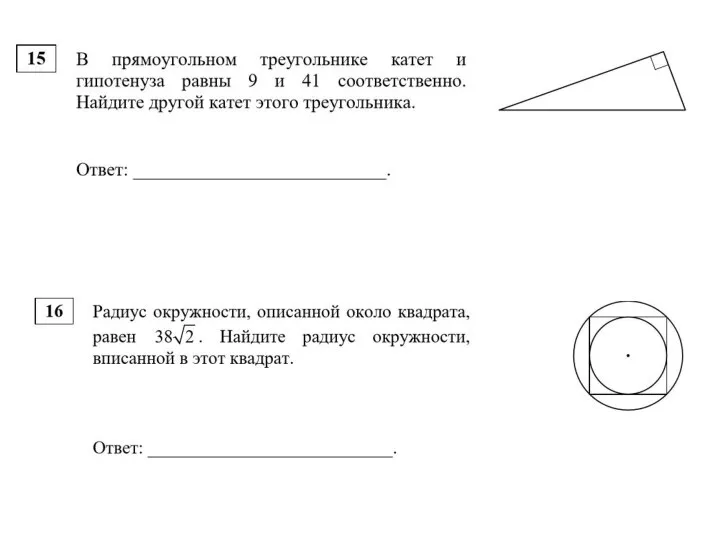 Решение задач
Решение задач