Презентация на тему Алгебра логики Логическое умножение, сложение и отрицание

Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составных высказываний, не вникая в их содержание.
В алгебре высказываний суждениям (простым высказываниям) ставятся в соответствие логические переменные, обозначаемые прописными буквами латинского алфавита.

Рассмотрим два простых высказывания:
А = «Два умножить на два равно четырем».
В = «Два умножить на два равно пяти».
В нашем случае первое высказывание истинно (А = 1), а второе ложно (В = 0).
В алгебре высказываний над высказываниями можно производить определенные логические операции, в результате которых получаются новые, составные высказывания.

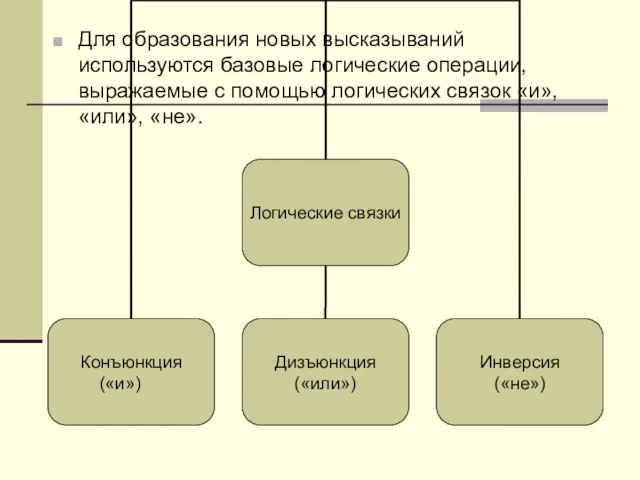
Для образования новых высказываний используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».

Логическое умножение (конъюнкция).
Объединение двух (или нескольких) высказываний в одно с помощью союза «и» называется операцией логического умножения или конъюнкцией.
Составное высказывание, образованное в результате операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.

Пример
(1) «2 - 2 = 5 и 3 • 3 = 10»,
(2) «2 • 2 = 5 и 3 • 3 = 9»,
(3) «2 -2 = 4 и 3 • 3 = 10»,
(4) «2 • 2 = 4 и 3 - 3 = 9».
Из этих высказываний истинно только (4)

Р = А & В.
С точки зрения алгебры высказываний мы записали формулу функции логического умножения, аргументами которой являются логические переменные А и В, которые могут принимать значения «истина» (1) и «ложь» (0).
Сама функция логического умножения Р также может принимать лишь два значения «истина» (1) и «ложь» (0).

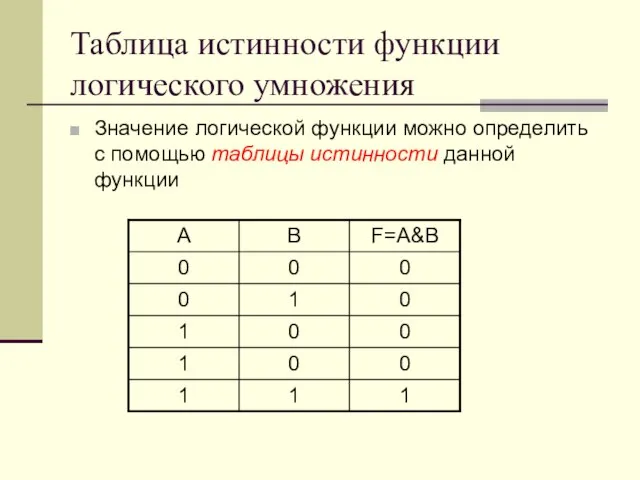
Таблица истинности функции логического умножения
Значение логической функции можно определить с помощью таблицы истинности данной функции

Логическое сложение (дизъюнкция)
Объединение двух (или нескольких) высказываний с помощью союза «или» называется операцией логического сложения или дизъюнкцией.
Составное высказывание, образованное в результате логического сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него простых высказываний.

Пример
(1) «2 • 2 = 5 или 3 • 3 = 10»,
(2) «2 • 2 = 5 или 3 • 3 = 9»,
(3) «2 • 2 = 4 или 3 • 3 = 10»,
(4) «2 • 2 = 4 или 3-3 = 9».
F = A B

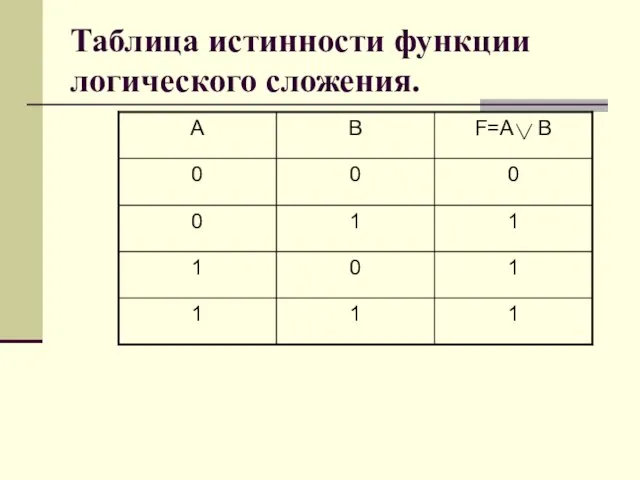
Таблица истинности функции логического сложения.

Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией логического отрицания или инверсией
Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное — истинным.

Пример
Пусть А = «Два умножить на два равно четырем» — истинное высказывание, тогда высказывание Р = «Два умножить на два не равно четырем», образованное с помощью операции логического отрицания, — ложно.
F = A