Содержание
- 2. Для работы с числами человек использует в основном две формы для их записи – естественную и
- 3. Целые числа. Целые числа без знака (только положительные) Целые числа со знаком (положительные и отрицательные) Для
- 4. Целые числа без знака. Обычно занимают в памяти один или два байта. В однобайтовом формате значения
- 5. Целые числа без знака. В двухбайтовом формате значения от 00000000 000000002 до 11111111 111111112 (0…65535) Пример
- 6. Целые числа со знаком. Обычно занимают в памяти компьютера 1, 2 или 4 байта, при этом
- 7. Целые числа со знаком. В однобайтовом формате значения от -128 до 127. В двухбайтовом формате значения
- 8. Целые числа со знаком. Примеры. 110=12 Знак числа «+»
- 9. Целые числа со знаком. В компьютерной технике применяются три формы записи (кодирования) целых отрицательных чисел: прямой
- 10. Прямой код числа. В знаковый разряд помещается цифра 1, а в разряды цифровой части – двоичный
- 11. Обратный код числа. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули
- 12. Дополнительный код числа. Получается образованием обратного кода с последующем прибавлением единицы к его младшему разряду. Пример
- 13. Как компьютер выполняет арифметические действия над целыми числами. В большинстве компьютеров операция вычитание не используется. Вместо
- 14. Примеры: 3 0 0000011 7 0 0000111 10 0 0001010 3 0 0000011 -10 1 1110101
- 15. Примеры: 10 0 0001010 -3 1 1111100 7 0 0000110 + + +1 0 0000111 Обратный
- 16. Примеры: -3 1 1111100 -7 1 1111000 -10 1 1110100 + + Обратный код числа -3
- 17. Задание 1. Представить число 21 в однобайтовой разрядной сетке.
- 19. Скачать презентацию
















 Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем
Анализ требований к программному обеспечению. Анализ и моделирование функциональной области внедрения программных систем Компьютерные сети
Компьютерные сети Инструкция по установке антивируса NOD32
Инструкция по установке антивируса NOD32 Графический редактор
Графический редактор Информационные технологии вокруг нас, в мире и в Беларуси
Информационные технологии вокруг нас, в мире и в Беларуси Технологія АТМ
Технологія АТМ Утилиты. Информационные технологии в профессиональной деятельности
Утилиты. Информационные технологии в профессиональной деятельности Виды пк в будущем
Виды пк в будущем Информация и человек. Виды информаций. Источники и приемники информации
Информация и человек. Виды информаций. Источники и приемники информации Проект Coursera
Проект Coursera Отчет об научно-исследовательской работе
Отчет об научно-исследовательской работе Наша группа
Наша группа Компьютерное информационное моделирование
Компьютерное информационное моделирование Как эффективно подать информацию
Как эффективно подать информацию Основы алгебры логики
Основы алгебры логики Компьютерные игры для девушек
Компьютерные игры для девушек Электронные деньги
Электронные деньги Полезные ресурсы (дизайнеры)
Полезные ресурсы (дизайнеры) Специализированные технические средства, применяемые в библиотеках
Специализированные технические средства, применяемые в библиотеках Порты ввода-вывода в компьютере
Порты ввода-вывода в компьютере Методика формирования библиографической компетентности
Методика формирования библиографической компетентности Основы работы в toondoo
Основы работы в toondoo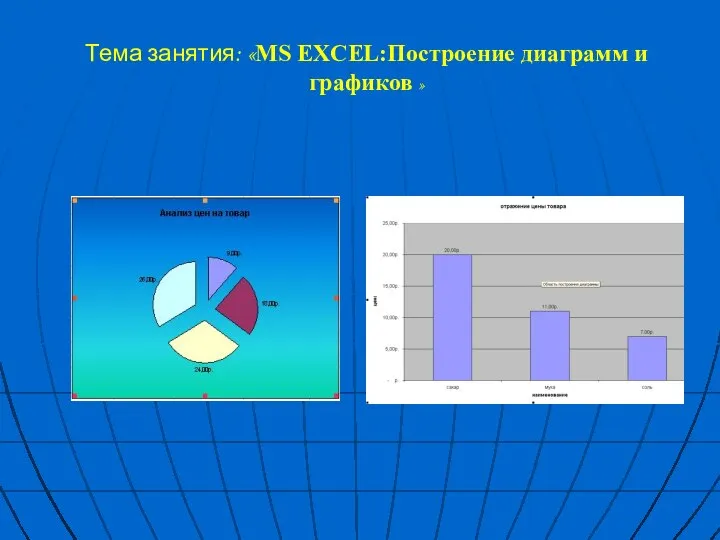 Ms Excel. Построение диаграмм и графиков
Ms Excel. Построение диаграмм и графиков События объекта TForm
События объекта TForm Шаблон. Применение шаблонов
Шаблон. Применение шаблонов Итог недели по созданию сайта для ООО Фирма ВиС
Итог недели по созданию сайта для ООО Фирма ВиС Основные виды
Основные виды Рисуем радугу
Рисуем радугу