Слайд 2Цель работы
Разработка структуры:
-минимальные затраты памяти;
-быстрый поиск;
-приоритезированный доступ.
Реализация структуры.
Анализ эффективности.
Визуализация.

Слайд 3Балансировка двоичных деревьев поиска
По высоте
По весу
По количеству узлов

Слайд 4Декартово дерево (Treap)
Декартово дерево - хранит пары (X,Y) в виде бинарного дерева
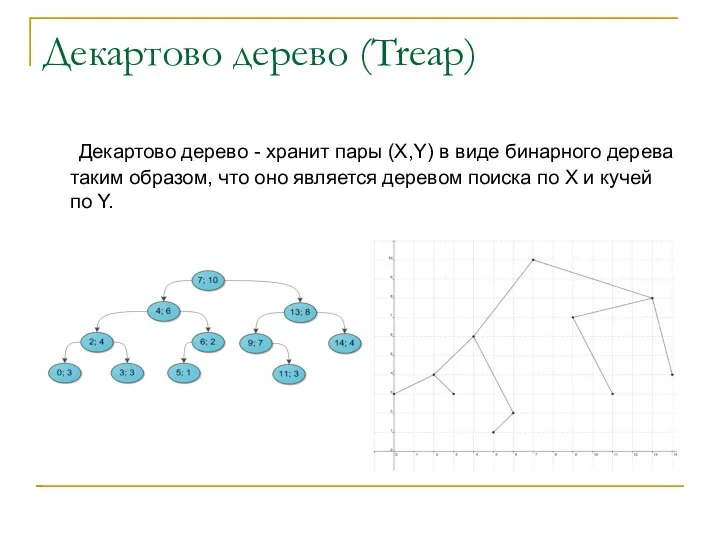
таким образом, что оно является деревом поиска по X и кучей по Y.
Слайд 5Структура данных TKOL
Разработанная структура, названная TKOL – двоичное дерево поиска, балансируемое по
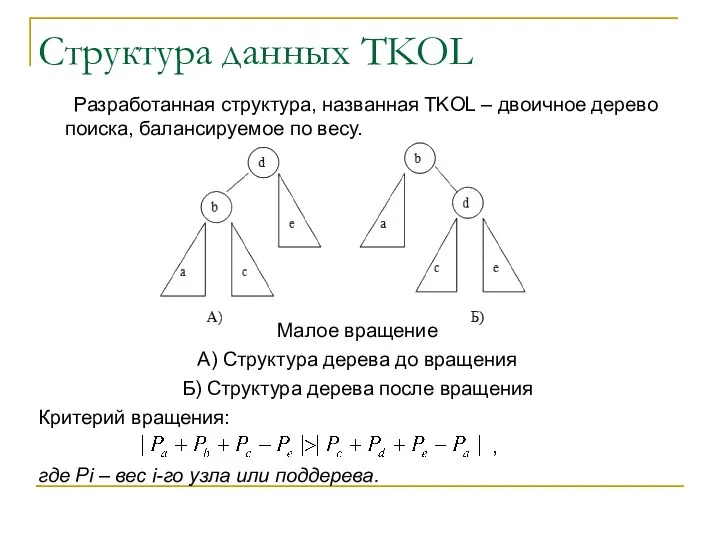
весу.
Малое вращение
А) Структура дерева до вращения
Б) Структура дерева после вращения
Критерий вращения:
,
где Pi – вес i-го узла или поддерева.
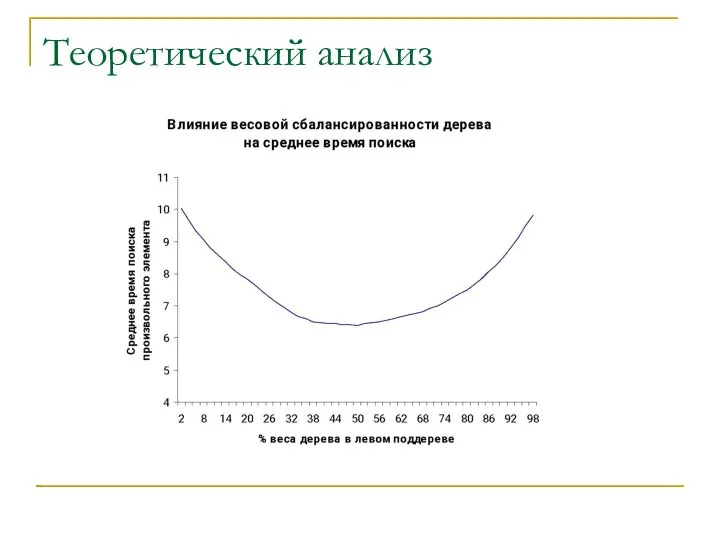
Слайд 6Теоретический анализ
Количество переходов по дереву до случайного элемента составляет
,
где:
- вес

левого поддерева;
- вес всего дерева;
- количество узлов в левом поддереве;
- суммарное количество узлов дерева.
Слайд 8Средневзвешенный путь
,
где Pi — собственный вес узла;
d — длина пути от

корня до узла, увеличенная на единицу.
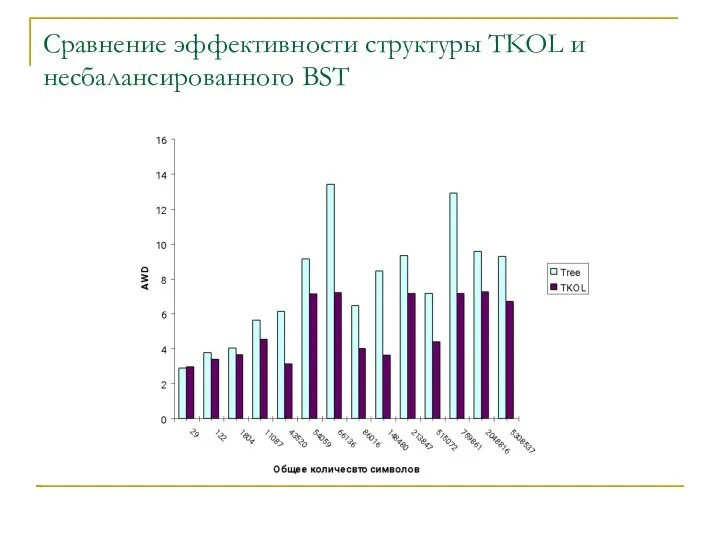
Слайд 9Сравнение эффективности структуры TKOL и несбалансированного BST







 Развитие экспорта медицинских услуг (Волгоградская область)
Развитие экспорта медицинских услуг (Волгоградская область) Документ и его создание
Документ и его создание Уроки практического программирования. Переменные и операторы
Уроки практического программирования. Переменные и операторы Цветовые модели компьютерной графики
Цветовые модели компьютерной графики Презентация на тему Устройство компьютера
Презентация на тему Устройство компьютера  Продвижение библиотеки в социальных сетях
Продвижение библиотеки в социальных сетях Алгоритм подачи заявки на ПФДО
Алгоритм подачи заявки на ПФДО Операторы цикла. Цикл с параметром. Операторы цикла итерационного типа
Операторы цикла. Цикл с параметром. Операторы цикла итерационного типа Блокированный жилой дом
Блокированный жилой дом Возможности воспроизведения звука в приложении Lazarus
Возможности воспроизведения звука в приложении Lazarus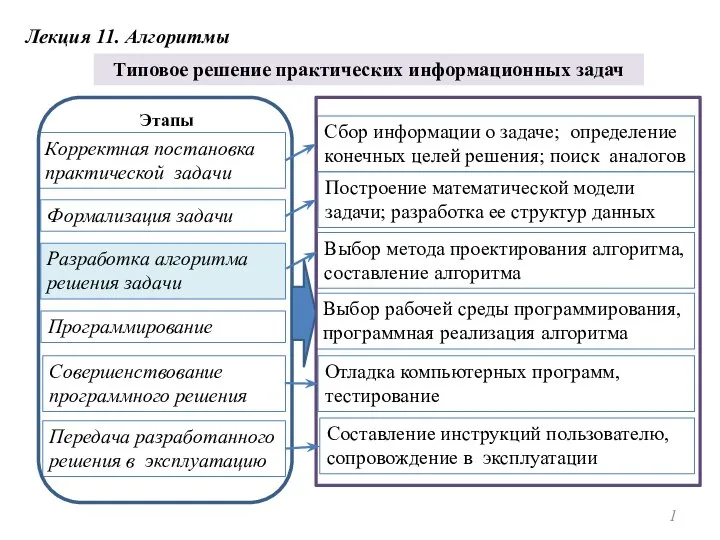 Алгоритмы. Типовое решение практических информационных задач
Алгоритмы. Типовое решение практических информационных задач Предметная неделя ИНФОРМАТИКИ
Предметная неделя ИНФОРМАТИКИ Запуск TDD LTE2300 на оборудовании AirScale
Запуск TDD LTE2300 на оборудовании AirScale Автоматизована інформаційно-довідкова система оздоровчого комплексу Енігма
Автоматизована інформаційно-довідкова система оздоровчого комплексу Енігма PDM/PLM - системы
PDM/PLM - системы Встроенные и логические функции в Excel
Встроенные и логические функции в Excel Что такое информация?
Что такое информация? Сортировка списков на языке Python
Сортировка списков на языке Python Представление числовых данных
Представление числовых данных Программирование – процес создания прорамм
Программирование – процес создания прорамм л2_сетевые приложения
л2_сетевые приложения Инструмент для создания цветовых комбинаций на базе исходного изображения
Инструмент для создания цветовых комбинаций на базе исходного изображения Геологическое картирование. Компьютерное сопровождение госгеолкарты-200
Геологическое картирование. Компьютерное сопровождение госгеолкарты-200 Преподаватель и студент в цифровом образовательном пространстве: опыт успешного взаимодействия
Преподаватель и студент в цифровом образовательном пространстве: опыт успешного взаимодействия Творческая работа по теме Сканирующие устройства
Творческая работа по теме Сканирующие устройства Теория игр. Аналитическая работа по статье Croson “Gender and Culture”
Теория игр. Аналитическая работа по статье Croson “Gender and Culture” Тема 6. Организация службы защиты информации (СЗИ)
Тема 6. Организация службы защиты информации (СЗИ) Количество информации. Системы счисления. Выполнение арифметических операций (задания)
Количество информации. Системы счисления. Выполнение арифметических операций (задания)