Содержание
- 2. Решение уравнений
- 3. Цели урока. Образовательные: построить алгоритм решения уравнения методом группировки известных и неизвестных слагаемых; формирование умения пользоваться
- 4. Повторение
- 5. Ответы к простейшим уравнениям а) x = 2,7 – 3,8 x = – 1,1 б) x
- 6. Оценивание «5» - верно решено 6 уравнений «4» - верно решено 4-5 уравнений «3» - верно
- 7. – Скажи мне знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы. – Вот
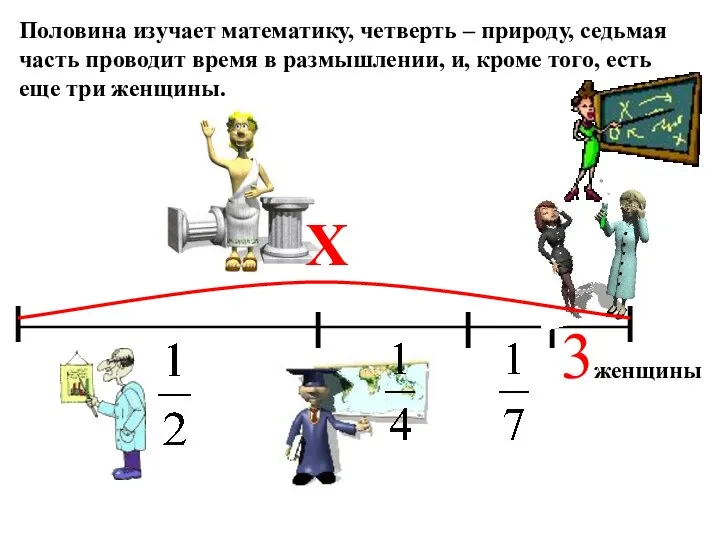
- 8. Половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и, кроме того, есть
- 9. Правило №1 В уравнении можно перенести слагаемое из одной части в другую, изменив при этом его
- 10. Правило №2 Обе части уравнения можно умножить или разделить на одно и то же число, отличное
- 11. Решение уравнения 3x – 6 = 5x Проверка: 3x – 5x = 6 3 ∙ (–
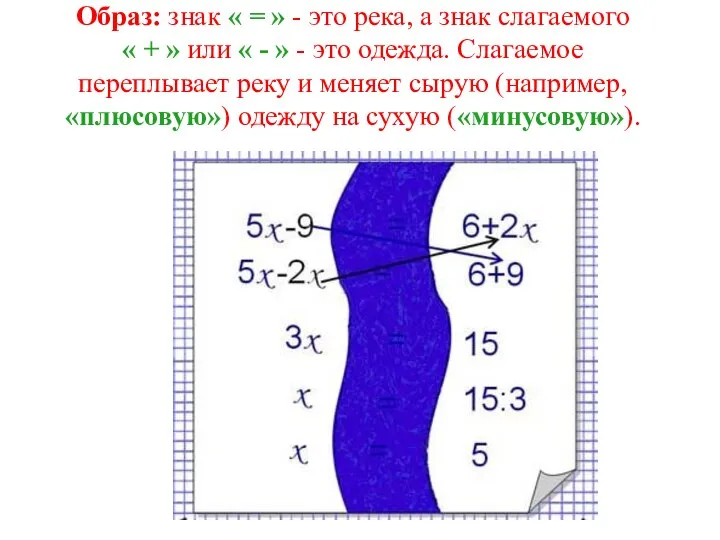
- 12. Образ: знак « = » - это река, а знак слагаемого « + » или «
- 13. Найди ошибку
- 14. Найди ошибку
- 15. Самостоятельная работа №2 I уровень. Заполни пропуски в решении уравнений. II уровень. Реши уравнения, используя приведённый
- 16. Дополнительное задание к самостоятельной работе
- 17. Решение древнегреческой задачи x = 1/2x + 1/4x + 1/7x + 3 x – 1/2x –
- 18. Старинная задача. Спросил некто учителя: «Скажи, сколько у тебя в классе учеников, так как хочу отдать
- 19. Дополнительная задача. Племянник спросил дядю, сколько ему лет. Дядя ответил: «Если к половине моих лет прибавить
- 20. Домашнее задание. 364, 365 (г-е), 347*. Творческое задание. Найти, решить и оформить старинную задачу, решаемую с
- 21. Список литературы. 1) Баврин И. И., Фрибус Е.А. Старинные задачи. М.: Просвещение, 1994. 2) Глейзер Г.И.
- 23. Скачать презентацию


















 Спрощення виразів. Підготовка до ЗНО
Спрощення виразів. Підготовка до ЗНО Решение задач
Решение задач Линии и углы в окружности
Линии и углы в окружности Деление десятичных дробей
Деление десятичных дробей Ортогональное проецирование на две взаимно перпендикулярные плоскости проекции
Ортогональное проецирование на две взаимно перпендикулярные плоскости проекции Спасение похищенных чисел. Урок-сказка
Спасение похищенных чисел. Урок-сказка Вероятность события (часть 1)
Вероятность события (часть 1) Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)
Презентация на тему Сложение дробей с одинаковыми знаменателями (4 класс)  Логарифмические уравнения
Логарифмические уравнения Элементы математической статистики
Элементы математической статистики Викторина по геометрии
Викторина по геометрии Написание цифр
Написание цифр Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM
Основы теории MOM метода. Настройка параметров EM симулятора на основе метода MOM Сложение в столбик
Сложение в столбик Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ  Математика в профессии Застройщик
Математика в профессии Застройщик Построение сечений многогранников
Построение сечений многогранников Правильные многоугольники
Правильные многоугольники Прибавление и вычитание числа 3. Помоги белочке
Прибавление и вычитание числа 3. Помоги белочке Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла
Геометрическое место точек. Построение серединного перпендикуляра и биссектриссы данного угла Интерактивный плакат: Многогранники
Интерактивный плакат: Многогранники Геометрические фигуры в жизни и в природе. Проект
Геометрические фигуры в жизни и в природе. Проект Симметрия вокруг нас
Симметрия вокруг нас Градусник. Приложение 2
Градусник. Приложение 2 Распредели предметы поровну
Распредели предметы поровну Презентация на тему Возведение в степень произведения и степени (7 класс)
Презентация на тему Возведение в степень произведения и степени (7 класс)  Закрепление решения задач на приведение к единице
Закрепление решения задач на приведение к единице Узагальнення і систематизація матеріалу по дробам
Узагальнення і систематизація матеріалу по дробам