Содержание
- 2. Задача 1. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Последовательность чисел Фибоначчи задается рекуррентным соотношением: F(1) =
- 3. Задача 1. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение. Условие k s+k=49+16=65 Ответ 65
- 4. Задача 2. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln('*');
- 5. Задача 2. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение1. сначала определим рекуррентную формулу; обозначим через G(n)
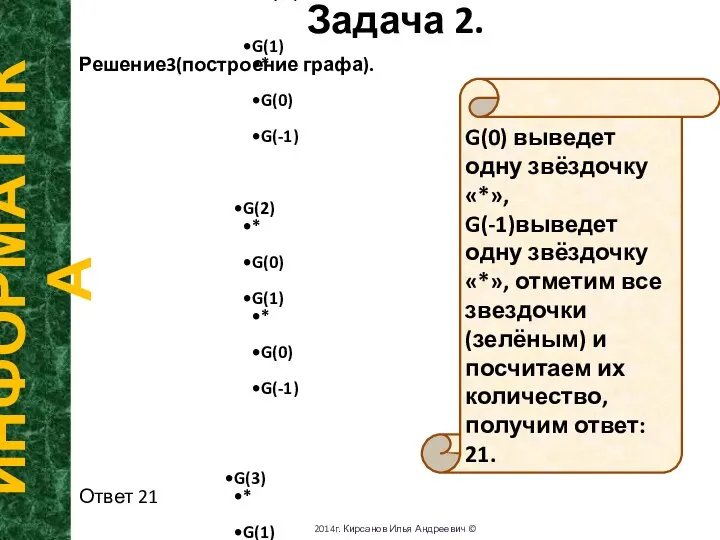
- 6. Задача 2. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Решение2(«с конца»). пп. 1-3 – как в варианте
- 7. G(0) выведет одну звёздочку «*», G(-1)выведет одну звёздочку «*», отметим все звездочки (зелёным) и посчитаем их
- 8. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln('*'); if
- 9. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Дан рекурсивный алгоритм: procedure f(n:integer); begin writeln(n); if n>0
- 10. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Алгоритм вычисления значения функции F(n) и G(n), где n
- 11. Вопросы. ИНФОРМАТИКА 2014г. Кирсанов Илья Андреевич © Последовательность чисел трибоначчи задается рекуррентным соотношением: F(1) = 0
- 13. Скачать презентацию









 Osnovnye_ponyatia_i_klassifikatsia_BD
Osnovnye_ponyatia_i_klassifikatsia_BD Лекция 1 мат. пакет Matlab (1)
Лекция 1 мат. пакет Matlab (1) Программное обеспечение компьютера
Программное обеспечение компьютера 1 урок химия осн (1)
1 урок химия осн (1)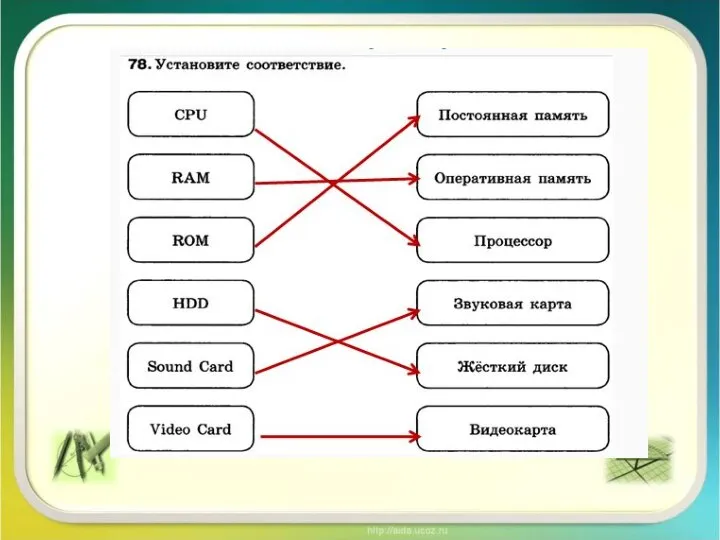 Виды памяти компьютера. Принцип работы. Урок 11
Виды памяти компьютера. Принцип работы. Урок 11 Multi-Factor Authentication Info Session Master
Multi-Factor Authentication Info Session Master Как проверить состоит ли ребенок в социальных сетях деструктивной направленности
Как проверить состоит ли ребенок в социальных сетях деструктивной направленности Microsoft Teams-гайд
Microsoft Teams-гайд Tutorial - How to remove search on Helios
Tutorial - How to remove search on Helios Перспективы развития информационных и коммуникационных технологий (ИКТ)
Перспективы развития информационных и коммуникационных технологий (ИКТ) Как сообщить об экстремистском контенте в социальных сетях
Как сообщить об экстремистском контенте в социальных сетях Использование модели глубокого обучения для предотвращения внезапных отказов разнородных объектов
Использование модели глубокого обучения для предотвращения внезапных отказов разнородных объектов Заметка в газету
Заметка в газету Проверка статуса запроса (заявления) online. Личный кабинет
Проверка статуса запроса (заявления) online. Личный кабинет Основы программирования на языке Pascal
Основы программирования на языке Pascal Анализ телеграм-канала Шум и я
Анализ телеграм-канала Шум и я Табулирование функций (без подпрограмм)
Табулирование функций (без подпрограмм) РћРњРћР__Лекция 2_Дискретные Рё непрерывные РјРѕРґРµРРё
РћРњРћР__Лекция 2_Дискретные Рё непрерывные РјРѕРґРµРРё Основы проектной деятельности
Основы проектной деятельности Образование в сфере IT
Образование в сфере IT Создание цветового портрета текста с помощью Wolfram Language
Создание цветового портрета текста с помощью Wolfram Language 2._
2._ Представление чисел в компьютере.10 класс
Представление чисел в компьютере.10 класс Назначение браузера
Назначение браузера Архитектурное решение по задаче Юридическая помощь
Архитектурное решение по задаче Юридическая помощь Методы и средства анализа безопасности программного обеспечения. Лк 4
Методы и средства анализа безопасности программного обеспечения. Лк 4 Локальные сети. 8 класс
Локальные сети. 8 класс Информационные системы на бумажных носителях. Способы организации данных
Информационные системы на бумажных носителях. Способы организации данных