Слайд 2
Геометрический метод решения ОЗЛП.
В практических задачах, как правило .
Предполагаем что ,

.
Выразим m базисных переменных через две свободных (например, и ). Система уравнений (2) примет вид:
(3)
Слайд 3С учетом условия неотрицательности переменных множество G можно представить в виде системы

неравенств:
(4)
Отложим по осям ОХ1 и ОХ2 значения свободных переменных, а также построим полуплоскости, соответствующие неравенствам (4):
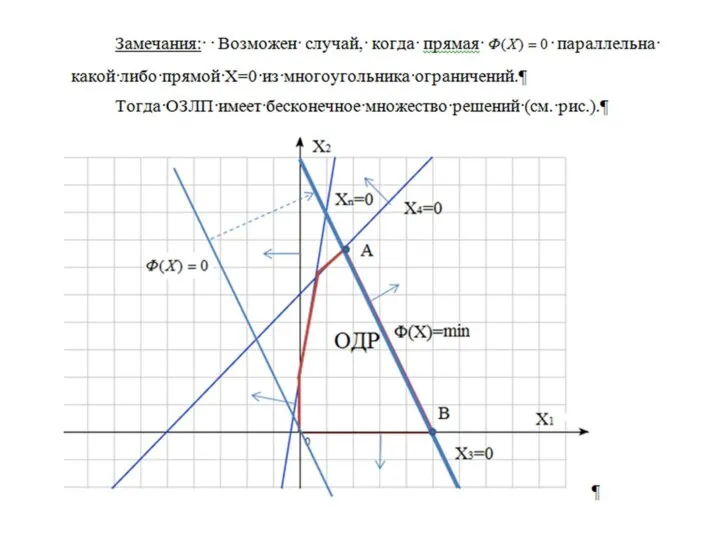
Слайд 5Утверждение. ОДР, если она существует, всегда является выпуклым множеством, имеющим форму многоугольника.
Поиск

оптимального решения.
Подставим соотношение (3) в (1).
Получим: . (5)
Будем рассматривать целевую функцию в виде:
, (6)
т.к. параметр a не влияет на оптимальное решение .
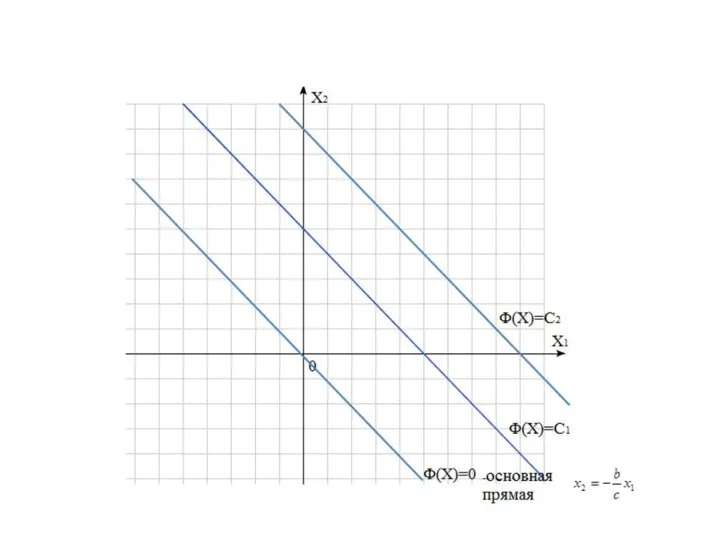
Слайд 6 Линии уровня целевой функции - параллельные прямые:
,
Изменение

параметра C равносильно мысленному перемещению прямой параллельно самой себе.
В каком направлении необходимо перемещать прямую , чтобы значение убывало?
Слайд 11Замечание: ОДР может быть неограниченным (незамкнутым) множеством. В этом случае возможна ситуация,

когда ОЗЛП не имеет конечного решения, т.е.
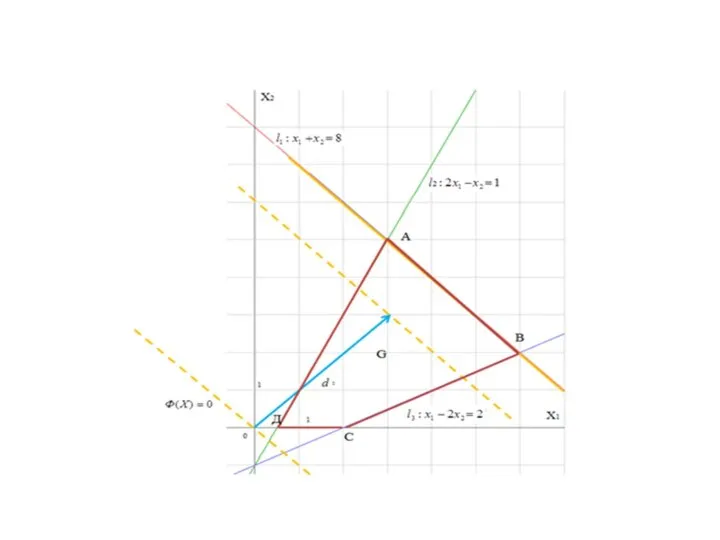
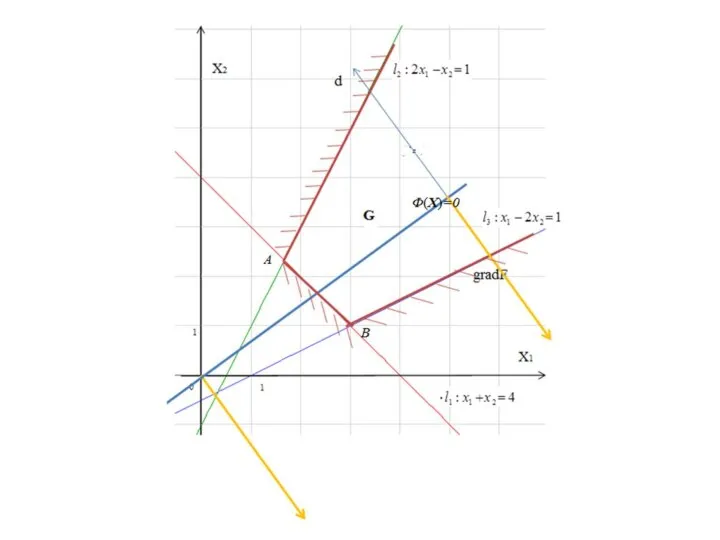
Слайд 22Задача 3.
Определить
при ограничениях:
Решение.
.
основные переменные;
свободные переменные .

Слайд 23Выразим основные переменные через свободные:
; .



















 Created by Itgenio. Переменные и типы данных
Created by Itgenio. Переменные и типы данных LR9-10_2ch__Diskretnoe_tsifrovoe_predstavlenie_textovoy_graficheskoy_zvukovoy_informatsii_i_videoinformatsii
LR9-10_2ch__Diskretnoe_tsifrovoe_predstavlenie_textovoy_graficheskoy_zvukovoy_informatsii_i_videoinformatsii KASIPKER. Маркетинг, каналы
KASIPKER. Маркетинг, каналы Роль и значение Web - технологий и компьютерной техники в лесном хозяйстве
Роль и значение Web - технологий и компьютерной техники в лесном хозяйстве Лекция 2. Классификация ПО
Лекция 2. Классификация ПО CPU ve Memory
CPU ve Memory Математические выражения на языке программирования. Самостоятельная работа
Математические выражения на языке программирования. Самостоятельная работа Разработка информационно-технологического обеспечения самодеятельного туризма
Разработка информационно-технологического обеспечения самодеятельного туризма Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Жанры тележурналистики
Жанры тележурналистики Разработка клиентской части база данных Магазин игрушек
Разработка клиентской части база данных Магазин игрушек Разработка электронного журнала успеваемости
Разработка электронного журнала успеваемости Социальные сети как способ коммуникации между участниками образовательного процесса
Социальные сети как способ коммуникации между участниками образовательного процесса Внедрение АИСУ в управление реализацией и сбытом готовой продукции
Внедрение АИСУ в управление реализацией и сбытом готовой продукции Массивы (двумерные)
Массивы (двумерные) Oracle Solaris
Oracle Solaris Неделя безопасного Рунета
Неделя безопасного Рунета Обзор системы команд процессора х386. Операнды в командах. (Лекция 5)
Обзор системы команд процессора х386. Операнды в командах. (Лекция 5) Системы счисления
Системы счисления Поисковые каналы изменили журналистику. Видео и трансляции, визуальная журналистика
Поисковые каналы изменили журналистику. Видео и трансляции, визуальная журналистика Полезные видеоблоги
Полезные видеоблоги WhatsApp ist ein beliebtes
WhatsApp ist ein beliebtes Программирование линейных алгоритмов
Программирование линейных алгоритмов Программное обеспечение модема
Программное обеспечение модема Язык гипертекстовой разметки HTML
Язык гипертекстовой разметки HTML Анализ уязвимостей драйверов
Анализ уязвимостей драйверов Язык запросов SQL
Язык запросов SQL Сравнительный анализ сайтов
Сравнительный анализ сайтов