Содержание
- 2. 1.2 Outguess. В качестве ПO используется цветное изображение в формате JPEG. Алгоритм реализован под операционную систему
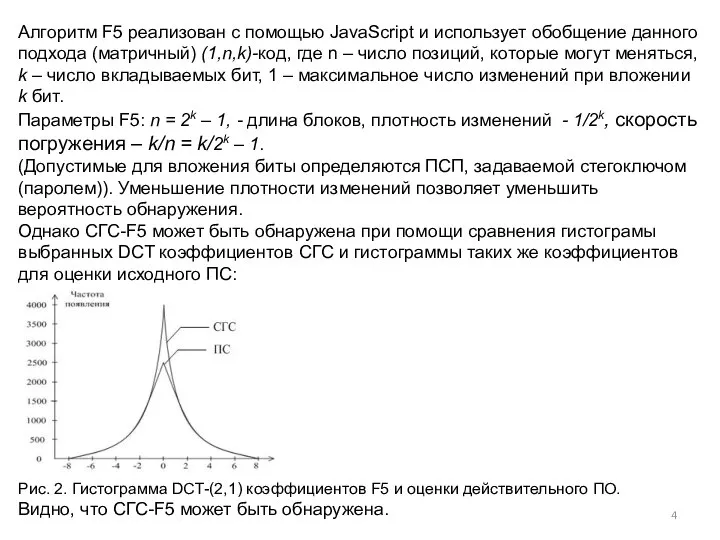
- 3. 1.3 F5. В качестве ПО используется цветное изображение в формате JPEG. Однако, в отличие от Jsteg
- 4. Алгоритм F5 реализован с помощью JavaScript и использует обобщение данного подхода (матричный) (1,n,k)-код, где n –
- 5. 2. СГС-ШПС. Все СГС-НЗБ не выдерживают атаки по удалению вложенных сообщений даже при сохранении при этом
- 6. Действительно, рассмотрим вероятность ошибки для легитимного пользователя, который знает π(n), n = 1,2…N. (4) При N
- 7. Положим сначала b = 0. Тогда (8) где Подставляя (5) и (6) в (8), получим (9)
- 8. Рассмотрим теперь случай информированного декодера, когда принятие решения о вложении информации выполняется по правилу: (14) где
- 9. Сравнивая p по (12) и p’ по (19) мы видим, что p ≥ p`. Действительно, выбирая
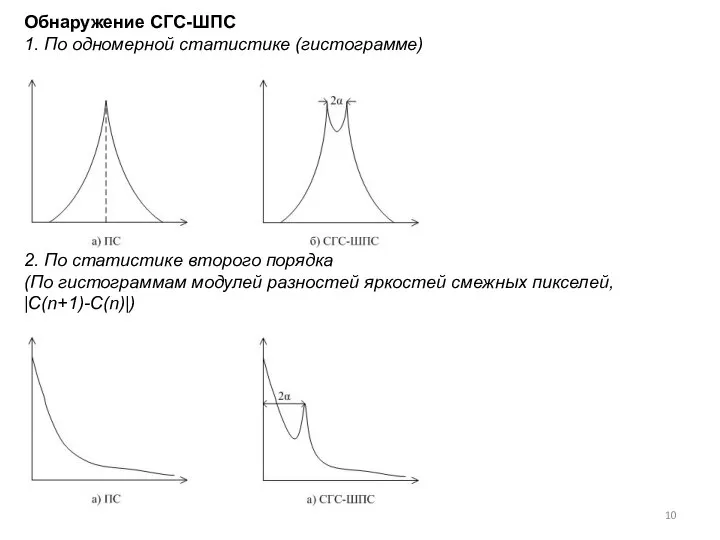
- 10. Обнаружение СГС-ШПС 1. По одномерной статистике (гистограмме) 2. По статистике второго порядка (По гистограммам модулей разностей
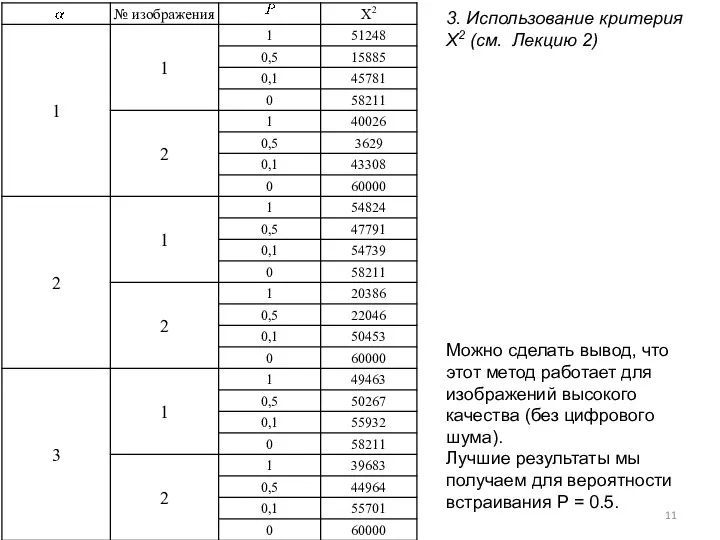
- 11. 3. Использование критерия X2 (см. Лекцию 2) Можно сделать вывод, что этот метод работает для изображений
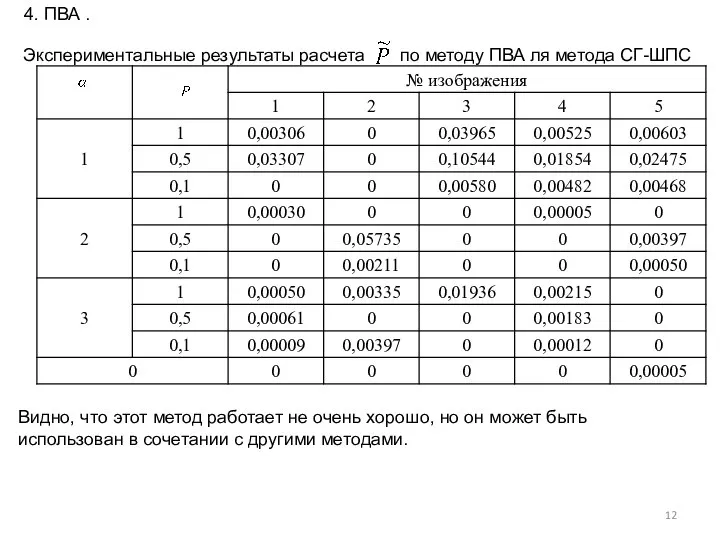
- 12. 4. ПВА . Видно, что этот метод работает не очень хорошо, но он может быть использован
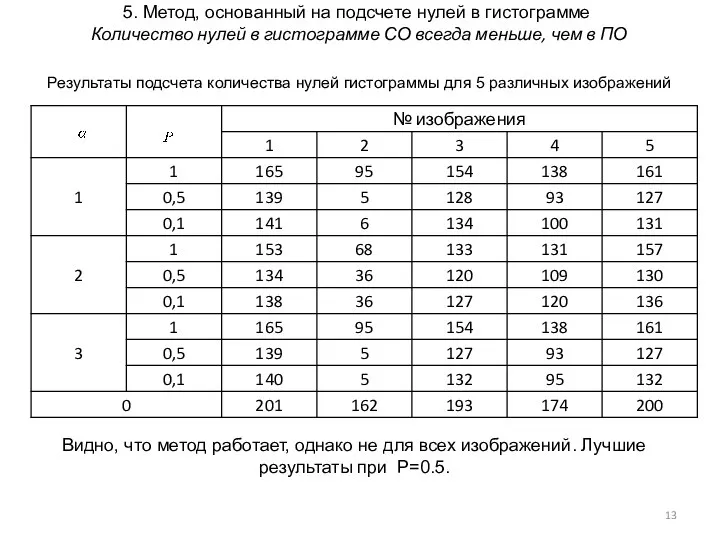
- 13. 5. Метод, основанный на подсчете нулей в гистограмме Количество нулей в гистограмме СО всегда меньше, чем
- 14. 6. По статистике суммы квадратов разностей яркостей соседних пикселей (21) где N0 – общее число пикселей
- 15. Замечание. Вложение ШПС-СГС по правилу (1) не обеспечит секретности, если при атаке известна , поскольку тогда
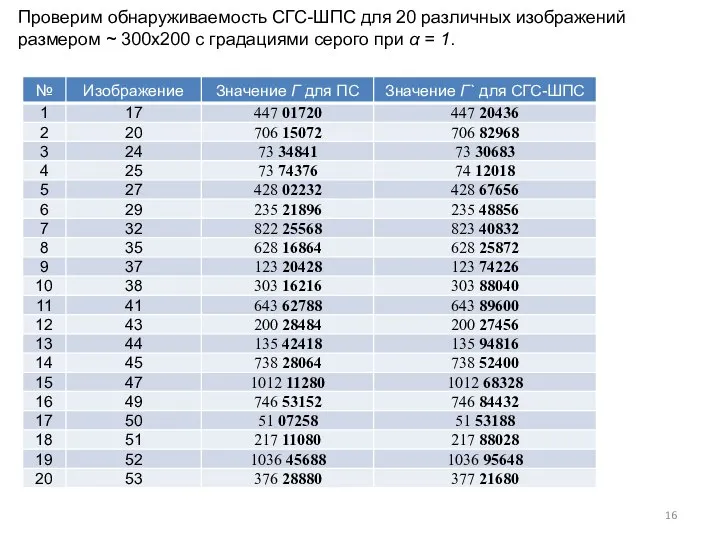
- 16. Проверим обнаруживаемость СГС-ШПС для 20 различных изображений размером ~ 300х200 с градациями серого при α =
- 18. Скачать презентацию









 Практическая квалификационная работа Устройство памяти персонального компьютера
Практическая квалификационная работа Устройство памяти персонального компьютера Табличный процессор MS Excel
Табличный процессор MS Excel Закрепление материала о Microsoft Word
Закрепление материала о Microsoft Word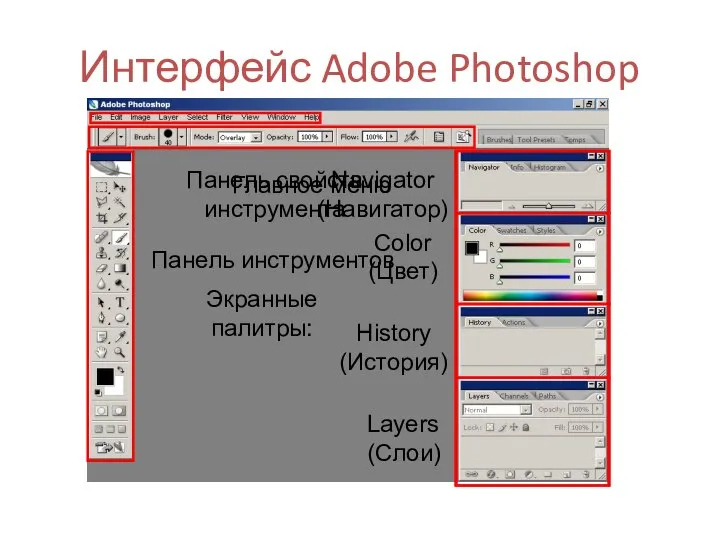 Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Программа мотивации 2019 год
Программа мотивации 2019 год Разновидности объектов и их классификация
Разновидности объектов и их классификация Тема 6.2 Параметры методов
Тема 6.2 Параметры методов Особенности использования функциональных возможностей MS Power Point при создании презентации
Особенности использования функциональных возможностей MS Power Point при создании презентации Работа CAE-систем. Пример SW. Информационные системы и технологии. (Лекция №2)
Работа CAE-систем. Пример SW. Информационные системы и технологии. (Лекция №2) Общие сведения о языке программирования Паскаль. Начала программирования
Общие сведения о языке программирования Паскаль. Начала программирования Подготовка к контрольной работе
Подготовка к контрольной работе КТ2
КТ2 Представление цифровой информации в компьютере
Представление цифровой информации в компьютере Портал Zakupay.pro
Портал Zakupay.pro Что такое пиксель? Видеомонтаж
Что такое пиксель? Видеомонтаж Введение в информатику. Лекция 1
Введение в информатику. Лекция 1 Фоны для ЛД
Фоны для ЛД Презентация на тему Рисуем в Word
Презентация на тему Рисуем в Word  Язык программирования Pascal Ветвление А. Жидков
Язык программирования Pascal Ветвление А. Жидков Роль информатики и информационных технологий в современном мире
Роль информатики и информационных технологий в современном мире Презентация на тему Алгоритм и его формальное исполнение
Презентация на тему Алгоритм и его формальное исполнение  Молодежный ТikТok канал как инструмент повышения мотивации к процессу обучения и саморазвитию
Молодежный ТikТok канал как инструмент повышения мотивации к процессу обучения и саморазвитию How much time do you spend online per day?
How much time do you spend online per day? Corrections Email Client (1)
Corrections Email Client (1) Как защитить ребенка от негативных факторов сети Интернет. Для родителей и учителей 4-5 класс
Как защитить ребенка от негативных факторов сети Интернет. Для родителей и учителей 4-5 класс Файлы и папки. Ваши данные на компьютере
Файлы и папки. Ваши данные на компьютере Правила работы в социальных сетях территориальных управлений и подведомственных учреждений Росприроднадзора
Правила работы в социальных сетях территориальных управлений и подведомственных учреждений Росприроднадзора Платформа бренда Вконтакте
Платформа бренда Вконтакте