Содержание
- 2. Тема занятия: Моделирование линейных звеньев Цели занятия: освоить построение основных характеристик непрерывных и дискретных линейных звеньев
- 3. Преобразование сигналов Любое обрабатывающее радиосигнал устройство может быть представлено как совокупность линейных и нелинейных звеньев Формально
- 4. Коэффициент передачи Линейное звено описывается дифференциальным уравнением: Нам достаточно научиться его решать для воздействия а потом
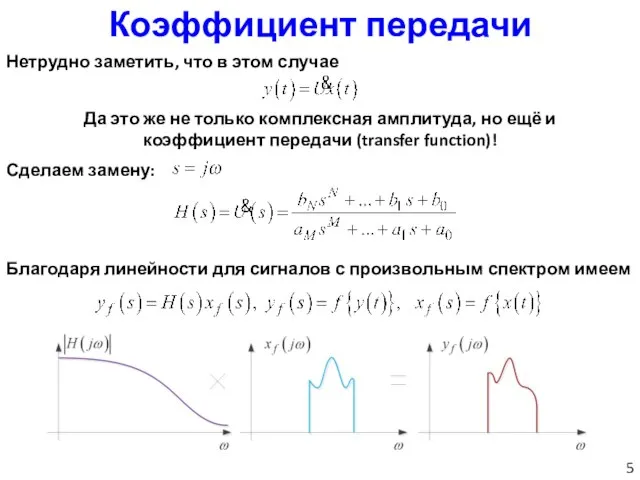
- 5. Коэффициент передачи Нетрудно заметить, что в этом случае Да это же не только комплексная амплитуда, но
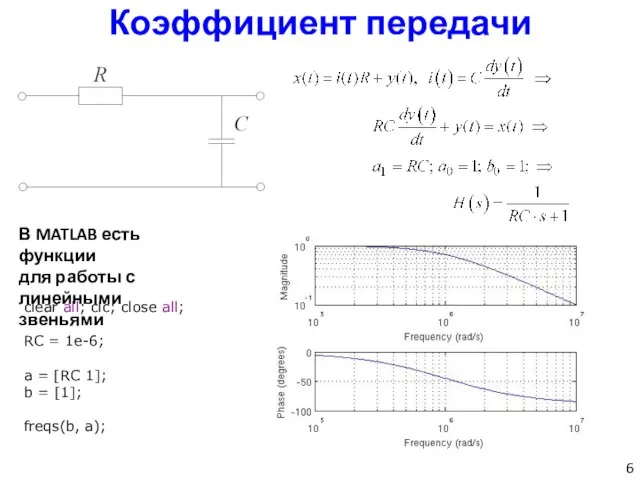
- 6. Коэффициент передачи clear all; clc; close all; RC = 1e-6; a = [RC 1]; b =
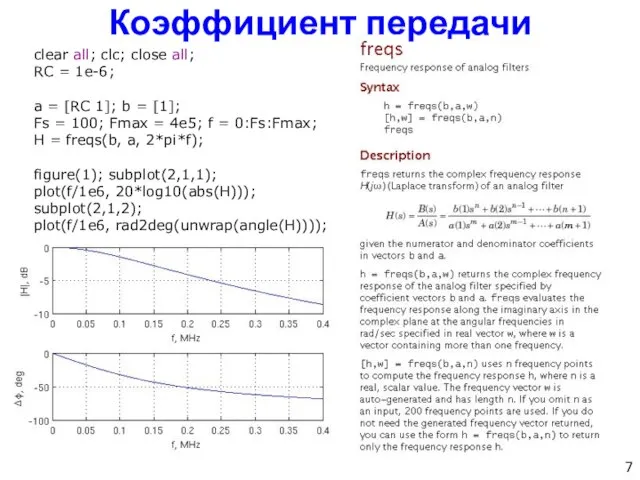
- 7. Коэффициент передачи clear all; clc; close all; RC = 1e-6; a = [RC 1]; b =
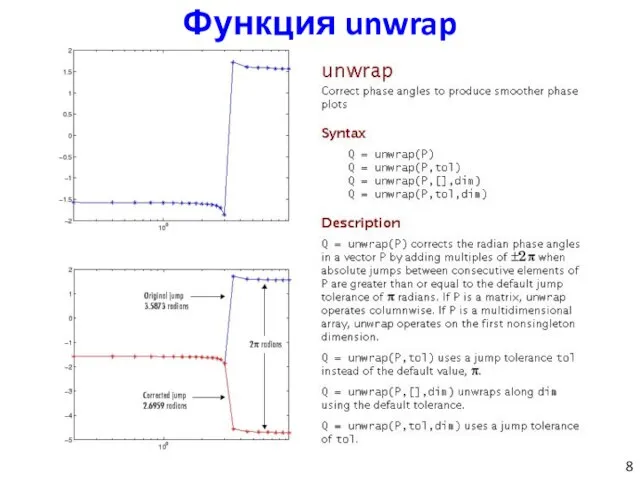
- 8. Функция unwrap
- 9. Импульсная характеристика (ИХ) А можно и через преобразование Лапласа: Умножению в частотной области соответствует свертка во
- 10. Импульсная характеристика Для построения импульсной характеристики можно воспользоваться функциями Сontrol System Toolbox RC = 1e-6; a
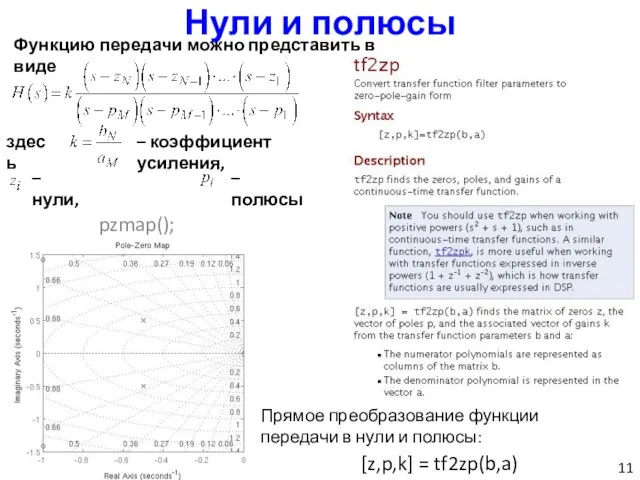
- 11. Нули и полюсы Функцию передачи можно представить в виде здесь – коэффициент усиления, – нули, –
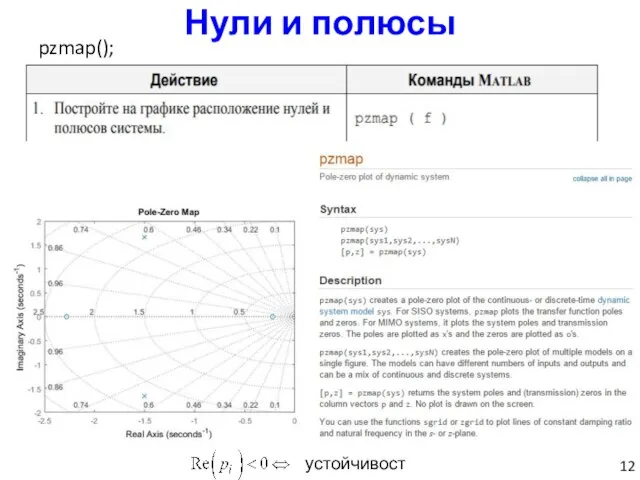
- 12. pzmap(); Нули и полюсы устойчивость
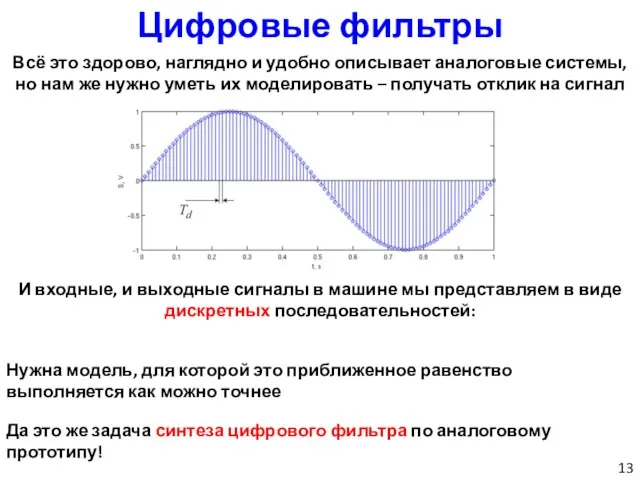
- 13. Цифровые фильтры Всё это здорово, наглядно и удобно описывает аналоговые системы, но нам же нужно уметь
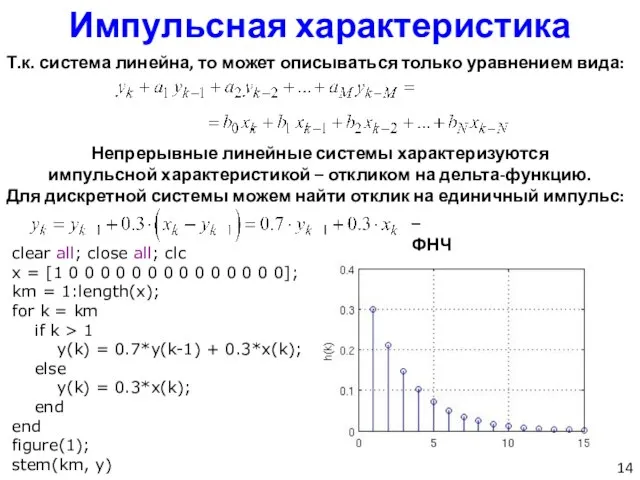
- 14. Импульсная характеристика Т.к. система линейна, то может описываться только уравнением вида: Непрерывные линейные системы характеризуются импульсной
- 15. impz(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; h = impz(b,
- 16. Transfer function Вспоминаем РЦС, z-преобразование и его свойства: Или из уравнения: Связь с преобразованием Фурье:
- 17. Transfer function clear all; close all; clc a = [-0.7]; b = [0.3]; xр = [1
- 18. freqz(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; H = freqz(b,
- 19. filter(…) clear all; close all; clc a = [1 -0.7]; b = [0.3]; x = [0
- 20. Нули и полюсы clear all; close all; clc a = [1 -0.7]; b = [0.3]; [z,
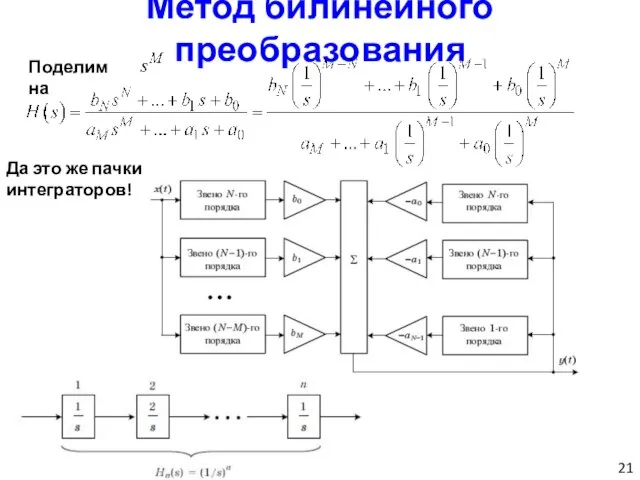
- 21. Метод билинейного преобразования Поделим на Да это же пачки интеграторов!
- 22. Метод билинейного преобразования А давайте аналоговый интегратор заменим цифровым! Интегрировать будем методом трапеций: Итого, в качестве
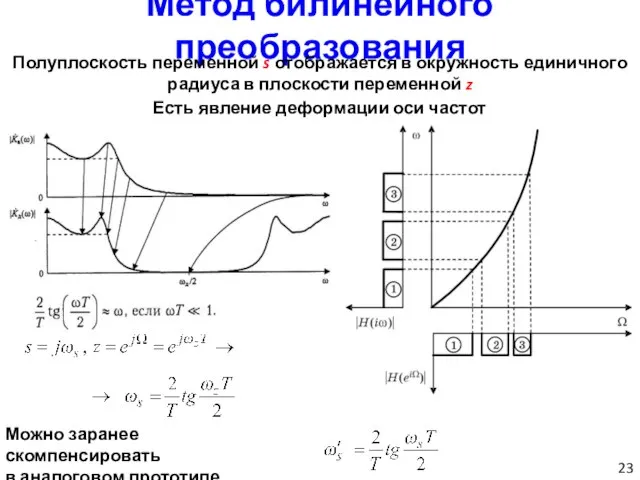
- 23. Метод билинейного преобразования Полуплоскость переменной s отображается в окружность единичного радиуса в плоскости переменной z Есть
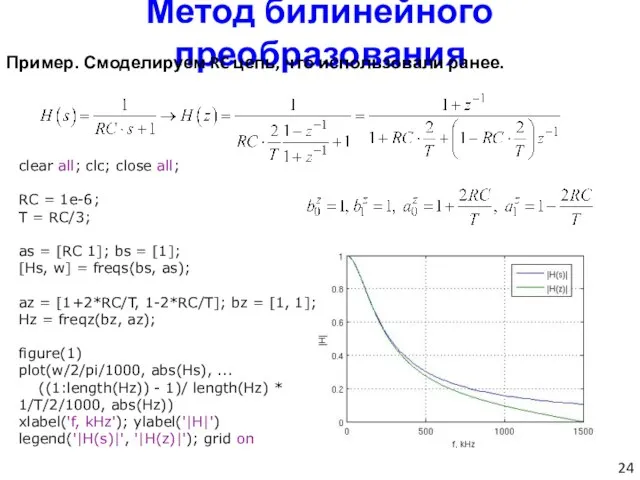
- 24. Метод билинейного преобразования Пример. Смоделируем RC цепь, что использовали ранее. clear all; clc; close all; RC
- 25. Билинейное преобразование - функция bilinear();
- 26. Практическая сторона дела Задача 5.1 Постановка задачи: В рамках лабораторной работы №1 проводилось моделирование участка электрической
- 27. Практическая сторона дела Задача 5.1 Постановка задачи (продолжение): Требуется: 2. найти характеристики дискретного фильтра, полученного методом
- 28. Практическая сторона дела Программа «PR5.m» clear all; clc; close all; tstart = tic(); % начало отсчета
- 29. Практическая сторона дела Продолжение программы «PR5.m» figure(2) subplot(2, 1, 1) semilogy(w/2/pi/1e6, abs(H)); xlabel('f, MHz'); ylabel('|H|') subplot(2,
- 30. Практическая сторона дела Продолжение программы «PR5.m» % Находим цифровой аналог Fs = 2 * wmax /
- 31. Практическая сторона дела Продолжение программы «PR5.m» f = 1e3; % Hz A = 1; E =
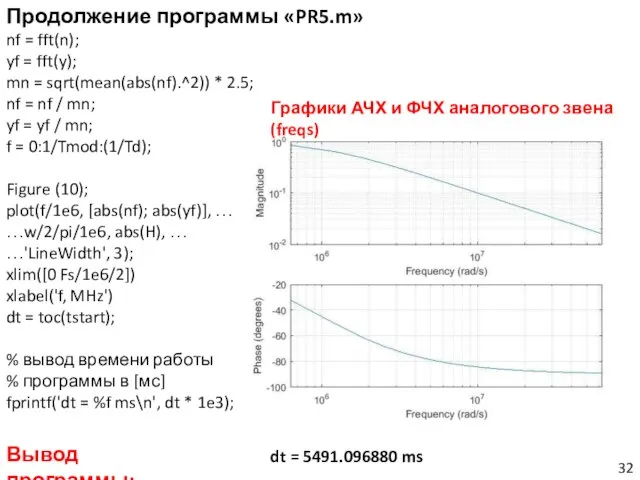
- 32. Продолжение программы «PR5.m» nf = fft(n); yf = fft(y); mn = sqrt(mean(abs(nf).^2)) * 2.5; nf =
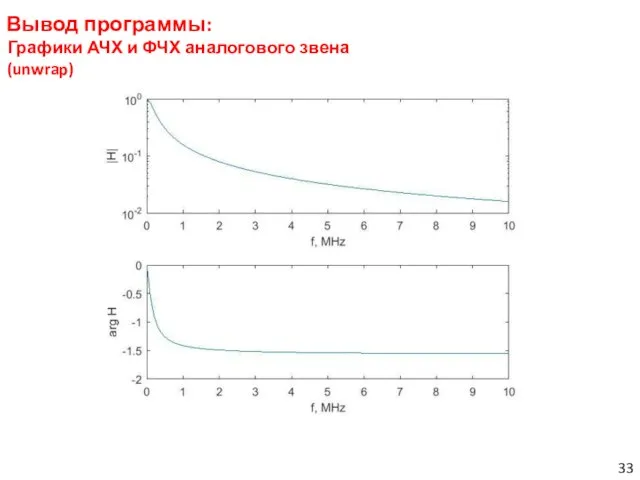
- 33. Вывод программы: Графики АЧХ и ФЧХ аналогового звена (unwrap)
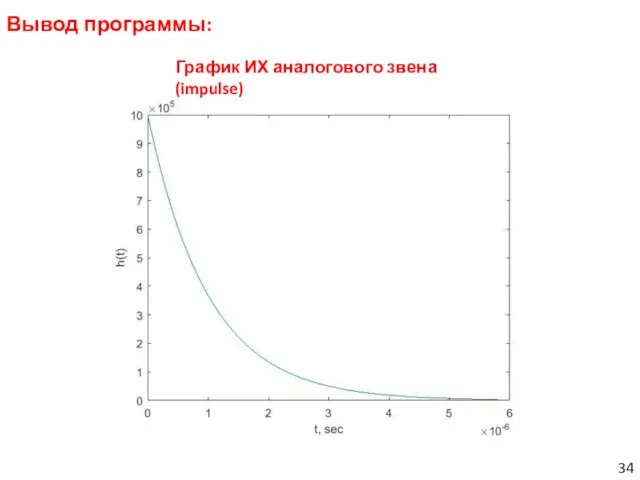
- 34. Вывод программы: График ИХ аналогового звена (impulse)
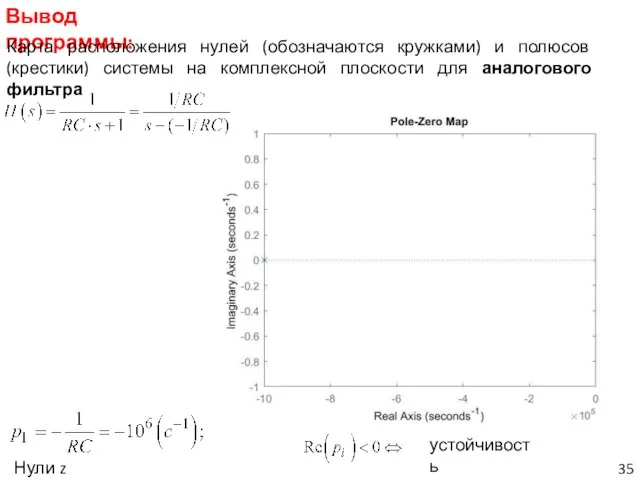
- 35. Вывод программы: Карта расположения нулей (обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости для аналогового
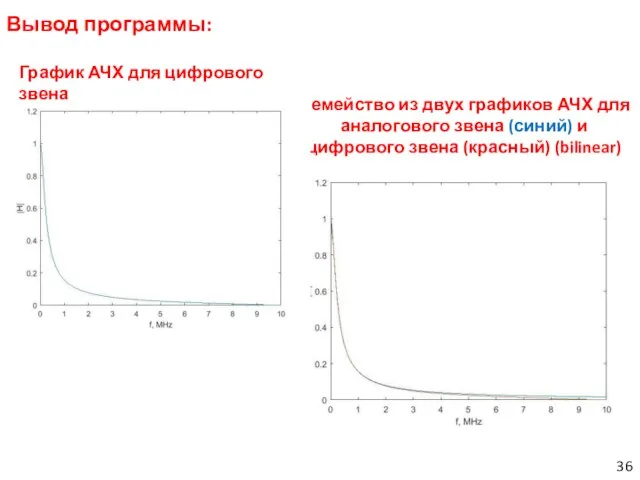
- 36. Вывод программы: Семейство из двух графиков АЧХ для аналогового звена (синий) и цифрового звена (красный) (bilinear)
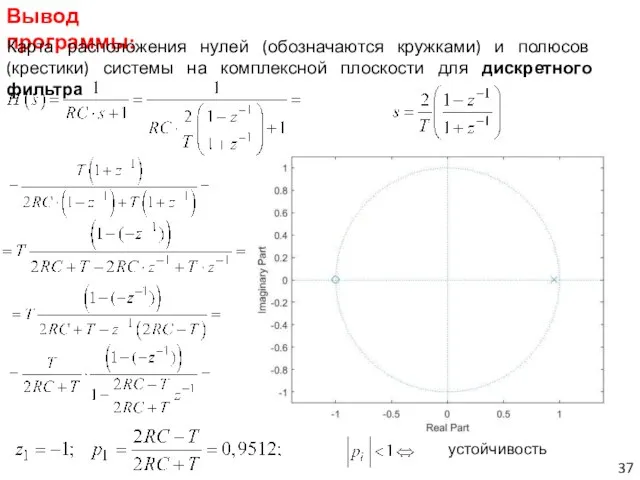
- 37. Вывод программы: Карта расположения нулей (обозначаются кружками) и полюсов (крестики) системы на комплексной плоскости для дискретного
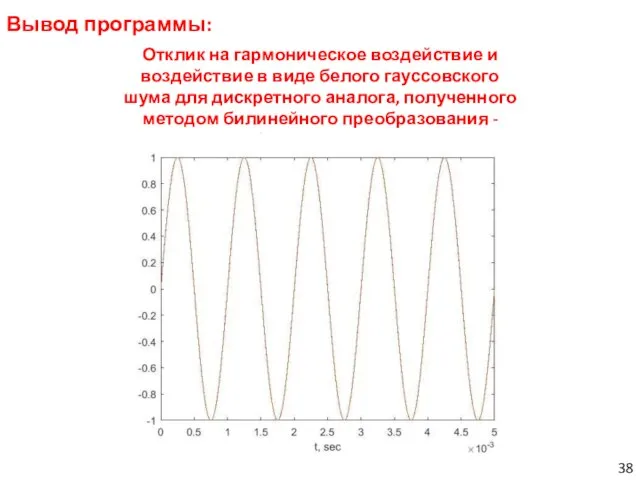
- 38. Вывод программы: Отклик на гармоническое воздействие и воздействие в виде белого гауссовского шума для дискретного аналога,
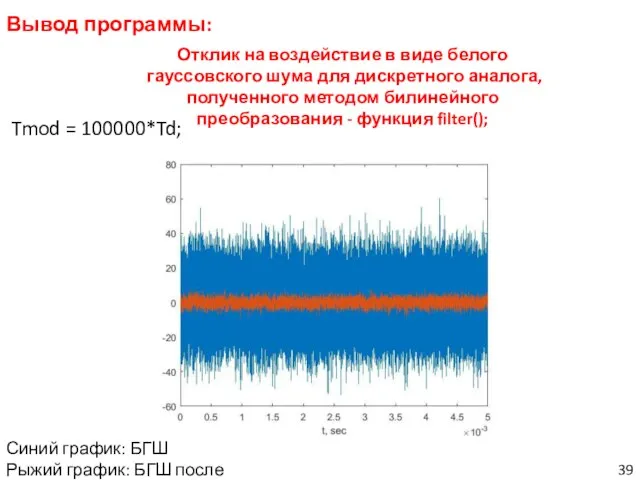
- 39. Вывод программы: Tmod = 100000*Td; Отклик на воздействие в виде белого гауссовского шума для дискретного аналога,
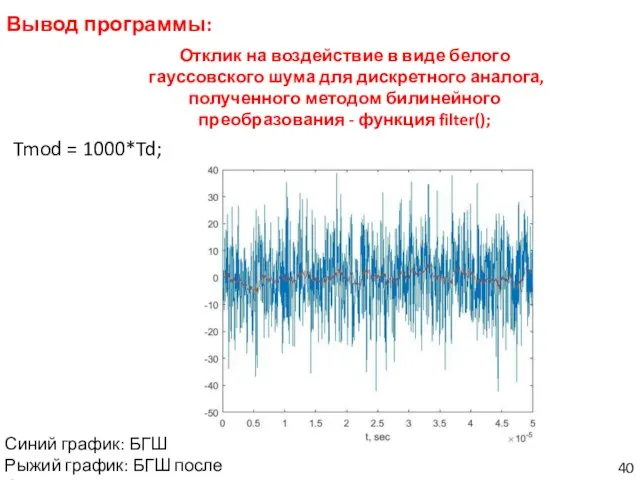
- 40. Вывод программы: Tmod = 1000*Td; Отклик на воздействие в виде белого гауссовского шума для дискретного аналога,
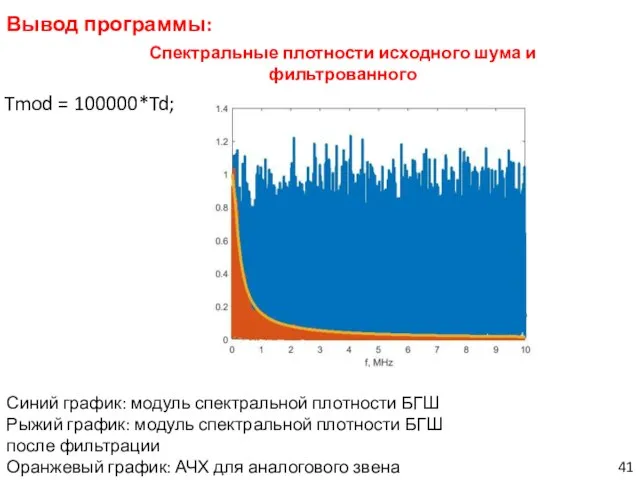
- 41. Вывод программы: Tmod = 100000*Td; Спектральные плотности исходного шума и фильтрованного Синий график: модуль спектральной плотности
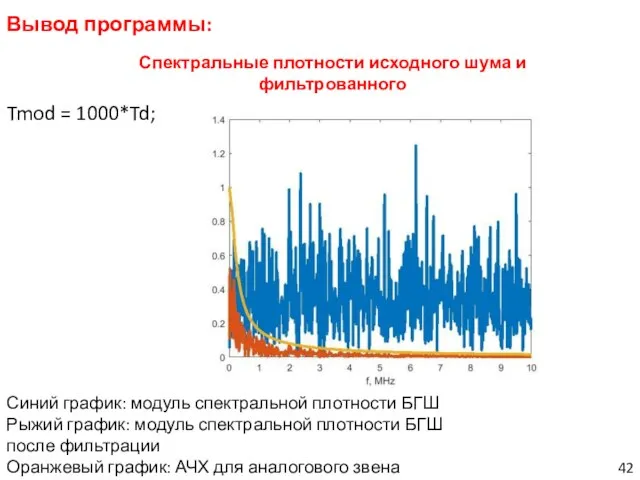
- 42. Вывод программы: Tmod = 1000*Td; Спектральные плотности исходного шума и фильтрованного Синий график: модуль спектральной плотности
- 44. Скачать презентацию





![impz(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876225/slide-14.jpg)

![Transfer function clear all; close all; clc a = [-0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876225/slide-16.jpg)
![freqz(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876225/slide-17.jpg)
![filter(…) clear all; close all; clc a = [1 -0.7]; b =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876225/slide-18.jpg)
![Нули и полюсы clear all; close all; clc a = [1 -0.7];](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/876225/slide-19.jpg)








 Знакомство с Visual Studio
Знакомство с Visual Studio Информационные системы и автоматизация информационных процессов
Информационные системы и автоматизация информационных процессов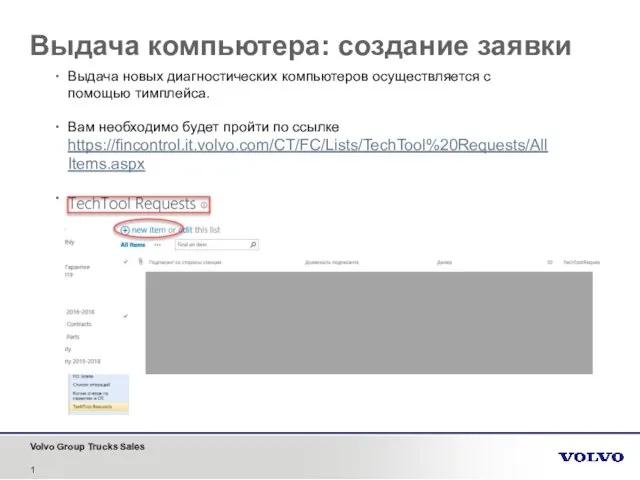 Выдача компьютера: создание заявки
Выдача компьютера: создание заявки Создание и заполнение баз данных. 9 класс
Создание и заполнение баз данных. 9 класс Интернет-проект История.ру
Интернет-проект История.ру Применение и наладка протоколов маршрутизации TCP, UDP, SCTP
Применение и наладка протоколов маршрутизации TCP, UDP, SCTP Свинограм
Свинограм Вставка в документ художественного текста и рисунков
Вставка в документ художественного текста и рисунков Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте
Проводник пассажирского вагона 3-го разряда с использованием социальной сети ВКонтакте Инструкция по обновлению навигационного ПО Hyundai Creta (GSr) with SD card
Инструкция по обновлению навигационного ПО Hyundai Creta (GSr) with SD card Программирование линейных алгоритмов. Начала программирования
Программирование линейных алгоритмов. Начала программирования Программирование в среде Robot C. Занятие 10: Структурное программирование
Программирование в среде Robot C. Занятие 10: Структурное программирование Формы мышления. Алгебра высказываний. Логические выражения и таблицы истинности
Формы мышления. Алгебра высказываний. Логические выражения и таблицы истинности Оператор Ввода
Оператор Ввода Презентация МДК
Презентация МДК Хищники. Культура и биология
Хищники. Культура и биология Правила поведения в чатах
Правила поведения в чатах Қазақстандағы байланыс қуралдарынын дамуы
Қазақстандағы байланыс қуралдарынын дамуы Устройства ввода графической информации. Итоговое тестирование
Устройства ввода графической информации. Итоговое тестирование Кодировка символов. Символьный тип. Строковые функции. Примеры. Лекция 4
Кодировка символов. Символьный тип. Строковые функции. Примеры. Лекция 4 Моделирование объектов виртуальной экспериментальной установки для лабораторной работы
Моделирование объектов виртуальной экспериментальной установки для лабораторной работы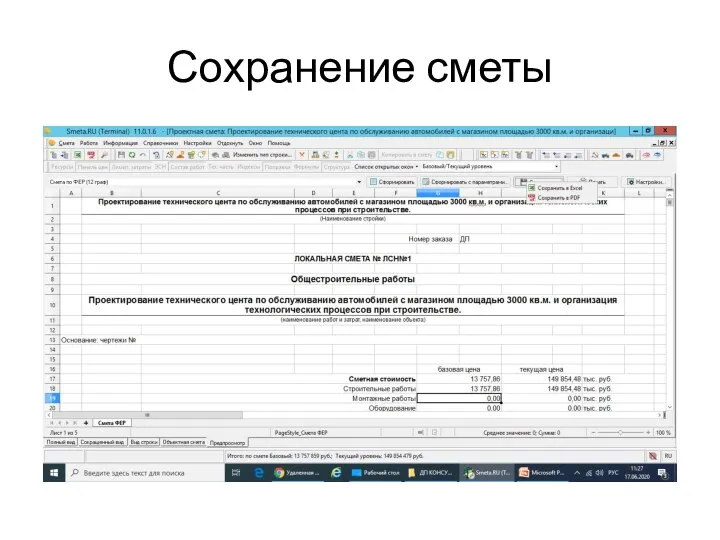 Сохранение сметы
Сохранение сметы Знаки и знаковые системы
Знаки и знаковые системы Путешествие в страну Занимательной грамматики
Путешествие в страну Занимательной грамматики Алгоритмы и их свойства
Алгоритмы и их свойства Tsoy
Tsoy Создание модели компьютерного класса будущего
Создание модели компьютерного класса будущего Принцип организации и преимущества колонки-ориентированной со сжатым словарем базы данных в памяти
Принцип организации и преимущества колонки-ориентированной со сжатым словарем базы данных в памяти