Программирование в MathCAD

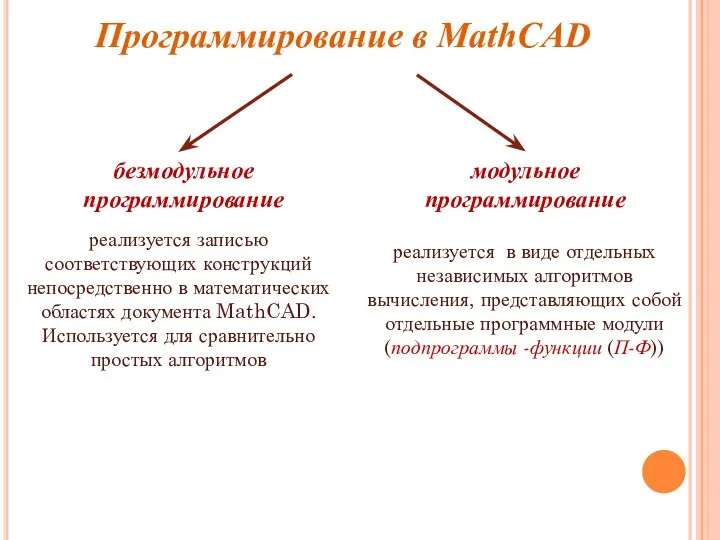
Программирование в MathCAD
безмодульное программирование
модульное программирование
реализуется записью соответствующих конструкций непосредственно в математических областях документа MathCAD. Используется для сравнительно простых алгоритмов
реализуется в виде отдельных независимых алгоритмов вычисления, представляющих собой отдельные программные модули (подпрограммы -функции (П-Ф))

Безмодульное программирование в MathCAD
Программирование линейных алгоритмов
Особенность: строго последовательное выполнение всех операций алгоритма без пропусков и повторений вычислений.
Проверка найденных корней:
Составить программу для вычисления корней квадратного уравнения

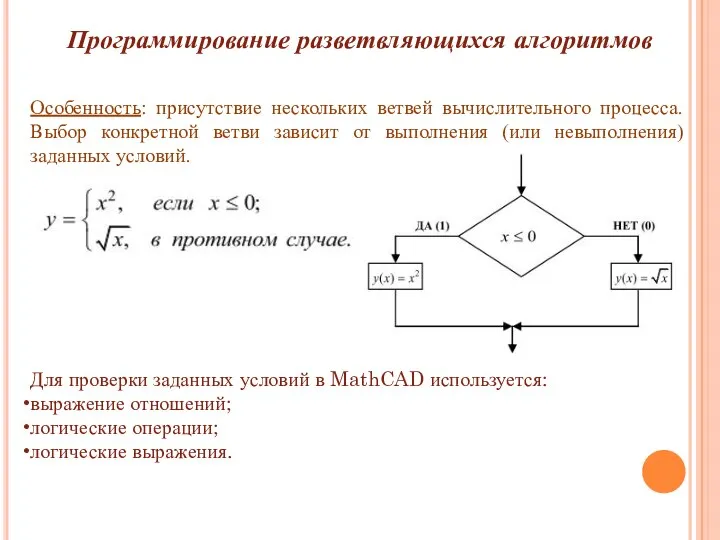
Программирование разветвляющихся алгоритмов
Особенность: присутствие нескольких ветвей вычислительного процесса. Выбор конкретной ветви зависит от выполнения (или невыполнения) заданных условий.
Для проверки заданных условий в MathCAD используется:
выражение отношений;
логические операции;
логические выражения.

Программирование разветвляющихся алгоритмов
Выражением отношений (или просто отношением) называется конструкция вида:
<выр.1> <операция отношения> <выр.2>
где <выр.1>, <выр.2> – произвольные арифметические выражения,
<операция отношения> – любая из следующих операций:
<│≤│>│≥│=│≠

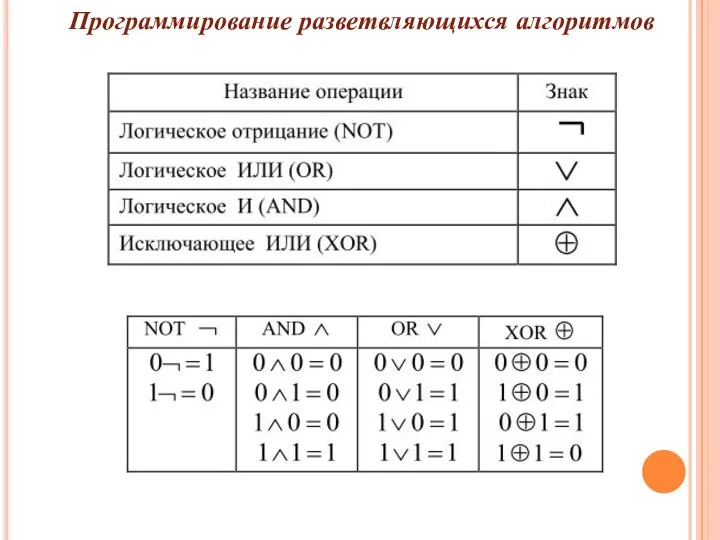
Программирование разветвляющихся алгоритмов

Программирование разветвляющихся алгоритмов
Логическое выражение – конструкция, состоящая из выражений отношений, логических операций и круглых скобок.
Принимает значения: 1 или 0.
Вычисляется слева направо с учетом приоритета входящих в выражение операций:
круглые скобки;
логическая операция И (AND);
логические операции ИЛИ (OR) и исключающая ИЛИ (XOR);
выражения отношений.

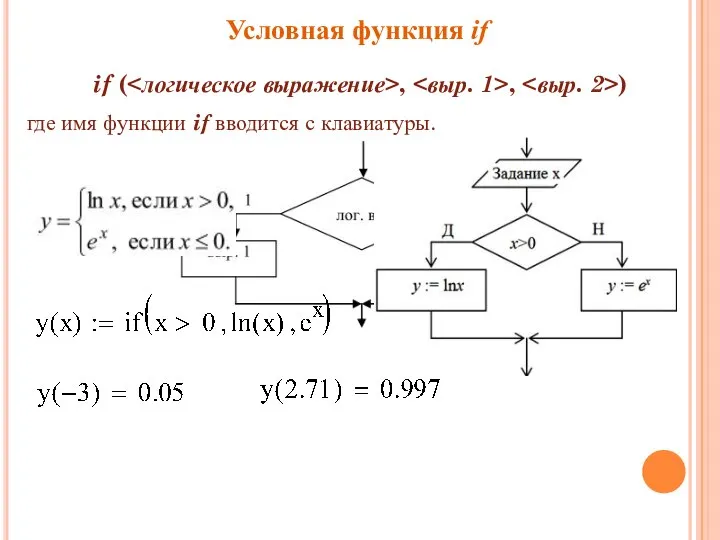
Условная функция if
if (<логическое выражение>, <выр. 1>, <выр. 2>)
где имя функции if вводится с клавиатуры.

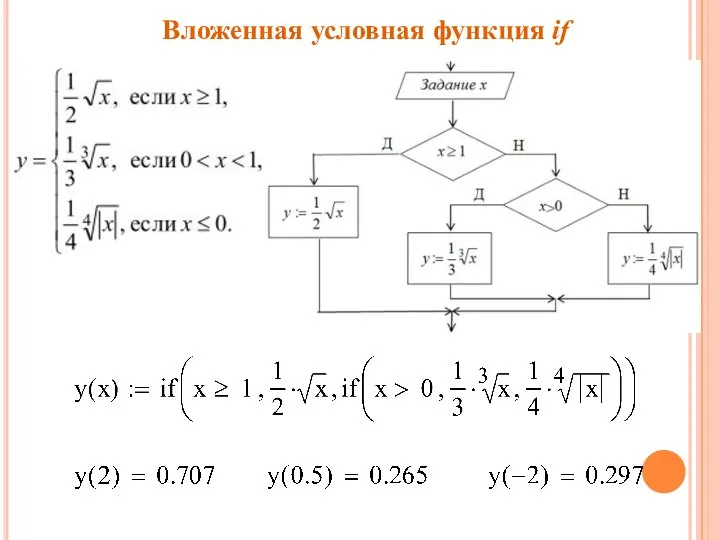
Вложенная условная функция if

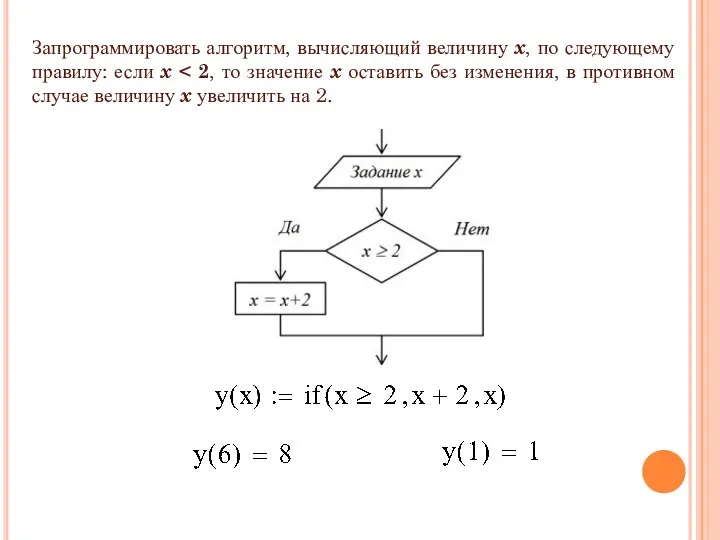
Запрограммировать алгоритм, вычисляющий величину x, по следующему правилу: если x < 2, то значение x оставить без изменения, в противном случае величину x увеличить на 2.

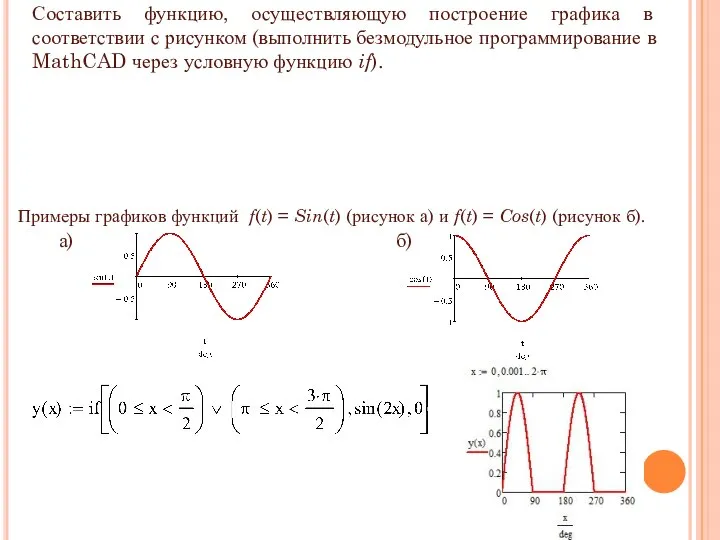
Составить функцию, осуществляющую построение графика в соответствии с рисунком (выполнить безмодульное программирование в MathCAD через условную функцию if).
Примеры графиков функций f(t) = Sin(t) (рисунок а) и f(t) = Cos(t) (рисунок б).
а) б)

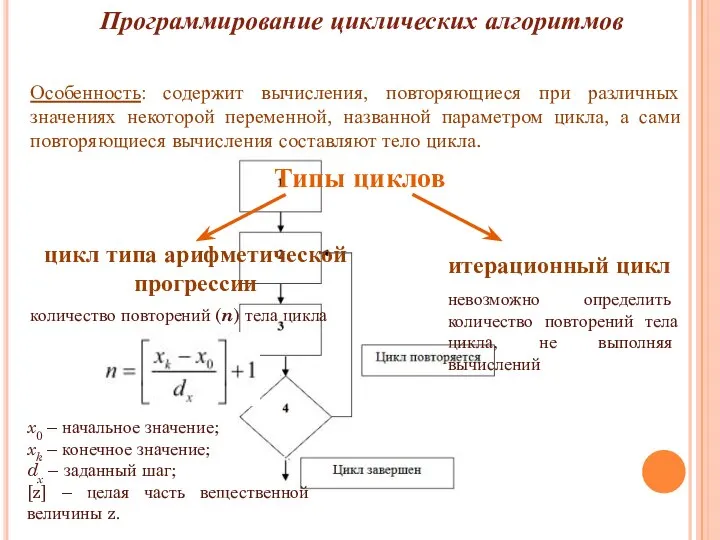
Программирование циклических алгоритмов
Особенность: содержит вычисления, повторяющиеся при различных значениях некоторой переменной, названной параметром цикла, а сами повторяющиеся вычисления составляют тело цикла.
Типы циклов
цикл типа арифметической прогрессии
итерационный цикл
x0 – начальное значение;
xk – конечное значение;
dx – заданный шаг;
[z] – целая часть вещественной величины z.
количество повторений (n) тела цикла
невозможно определить количество повторений тела цикла, не выполняя вычислений

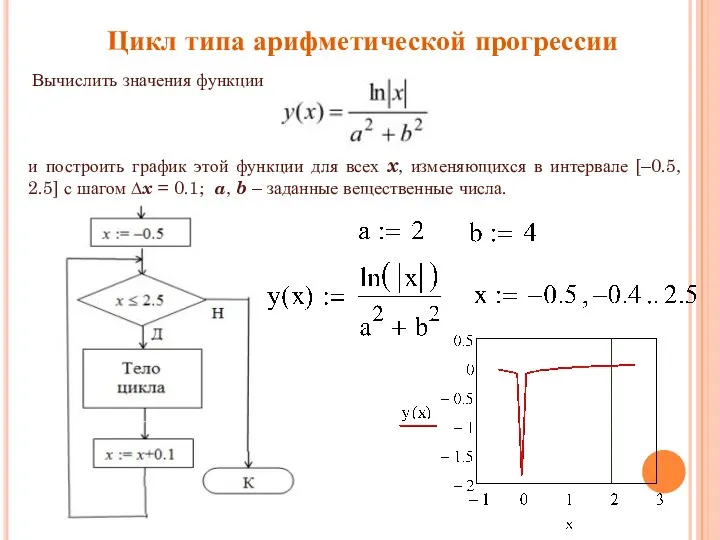
Цикл типа арифметической прогрессии
Вычислить значения функции
и построить график этой функции для всех x, изменяющихся в интервале [–0.5, 2.5] с шагом ∆x = 0.1; a, b – заданные вещественные числа.

Сформировать матрицу (двумерный массив) В по следующему правилу:
Цикл типа арифметической прогрессии