Шейкерная сортировка ShakerSort

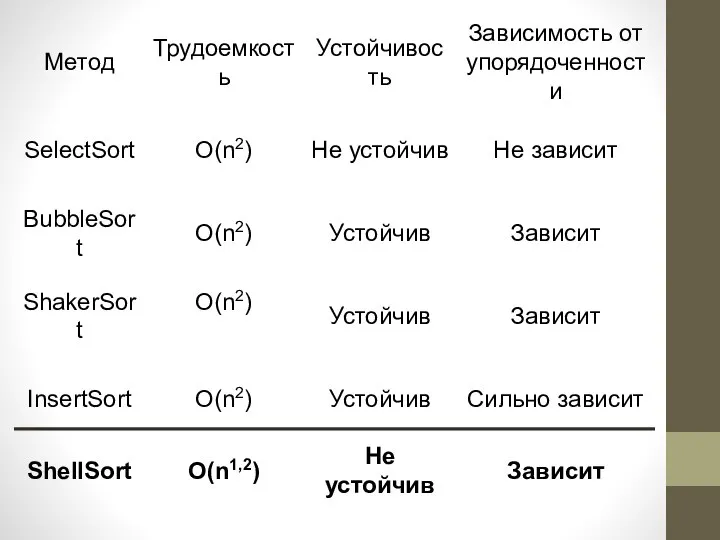
Шейкерная сортировка ShakerSort
ДВА (!) изменения в алгоритме, которые были предложены для уменьшения трудоемкости:
1) Изменение направления просмотра массива на каждой итерации.
2) Установление границ рабочей части массива на место последнего обмена на каждой итерации.

Шейкерная сортировка ShakerSort
Алгоритм на псевдокоде
L, R – левая и правая границы рабочей части массива,
n – количество элементов в массиве.
L := 1, R := n, k := n,
DO
DO ( j := R, R-1, ... L+1)
IF (aj < aj-1) aj↔aj-1, k := j FI
OD
L := k
DO ( j := L, L+1, ... R-1)
IF (aj > aj+1) aj↔aj+1, k := j FI
OD
R := k
OD (L < R)

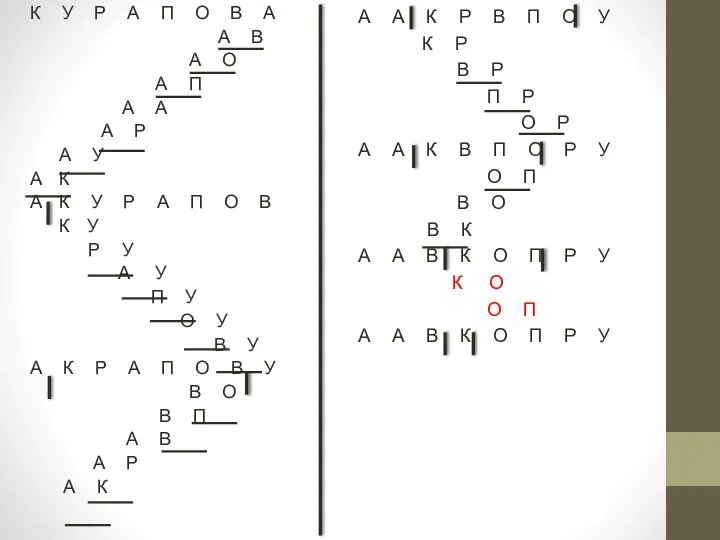
К У Р А П О В А
А В
А О А П
А А
А Р
А У
А К
А К У Р А П О В
К У
Р У
А У
П У
О У
В У
А К Р А П О В У
В О
В П
А В
А Р
А К
А А К Р В П О У
К Р
В Р
П Р
О Р
А А К В П О Р У
О П
В О
В К
А А В К О П Р У
К О
О П
А А В К О П Р У

Видео:
BubbleSort или ShakerSort ?

Метод прямого включения
InsertSort
Начиная с i = 2 берём очередной i–й элемент массива и включаем его на нужное место среди первых (i-1) элементов, при этом все элементы, которые больше ai сдвигаются на одну позицию вправо.

Метод прямого включения
Алгоритм на псевдокоде
DO ( i: = 2, 3, …, n )
t := ai, j := i -1
DO ( j > 0 и t < aj )
aj+1 := aj
j := j -1
OD
aj+1 := t
OD

К У Р А П О В А
К У Р А П О В А
К Р У А П О В А
А К Р У П О В А
А К П Р У О В А
А К О П Р У В А
А В К О П Р У А
А А В К О П Р У

Видео:
InsertSort

Метод Шелла
ShellSort
Из оценок метода прямого включения InsertSort видно, что, чем лучше упорядочен массив, тем меньше операций потребуется для его сортировки.
Основная идея метода Шелла ShellSort состоит в предварительном улучшении порядка элементов массива, а затем окончательной сортировке его методом прямого включения.
Шелл предложил работать в методе прямого включения с шагом k большим, чем 1, что предварительно улучшило бы упорядоченность массива.
Чем больше величина шага, тем меньше операций сравнения и пересылки приходиться выполнять.

Определение Предварительная сортировка массива методом прямого включения с шагом к > 1 называется к - сортировкой.
Метод Шелла заключается в проведении сначала нескольких к-сортировок, а затем окончательной сортировке массива с шагом к=1.
Обозначим
H = ( h1 , h2 , … , hm ) – последовательность из m возрастающих шагов, где h1 = 1, h1 < h2 < h3 < …< hm .
Производя последовательно к-сортировки с шагами hm , hm-1 ,.., h1 , получим упорядоченный массив. Это гарантируется тем, что последний шаг h1 = 1.

Метод Шелла (ShellSort)
Алгоритм на псевдокоде
<вычисление массива шагов h>
DO ( k := hm , hm-1 , … 1 )
DO ( i := k+1, k+2, … n )
t := ai , j := i - k
DO ( j > 0 и t < aj )
aj+k := aj
j := j - k
OD
aj+k := t
OD
OD

К У Р А П О В А
К У Р А П О В А
К А Р У П О В А
К А П У Р О В А
К А П О Р У В А
В А К О П У Р А
В А К А П О Р У

В А К А П О Р У
А В К А П О Р У
А В К А П О Р У
А А В К П О Р У
А А В К П О Р У
А А В К О П Р У
А А В К О П Р У

При использовании последовательности шагов, предложенной Д.Кнутом, метод имеет порядок трудоёмкости O ( n1.2 ) , n→∞.
Метод Шелла существенно быстрее методов с квадратичной трудоемкостью.
В примере: Insert – 46 операций,
Shell – 34 операции.
Метод Шелла не устойчив.
Метод зависит от исходной упорядоченности массива.