Содержание
- 2. 3. Определенной функцией, которая отображает зависимость выходного сигнала от входных. В мире применяют две системы условных
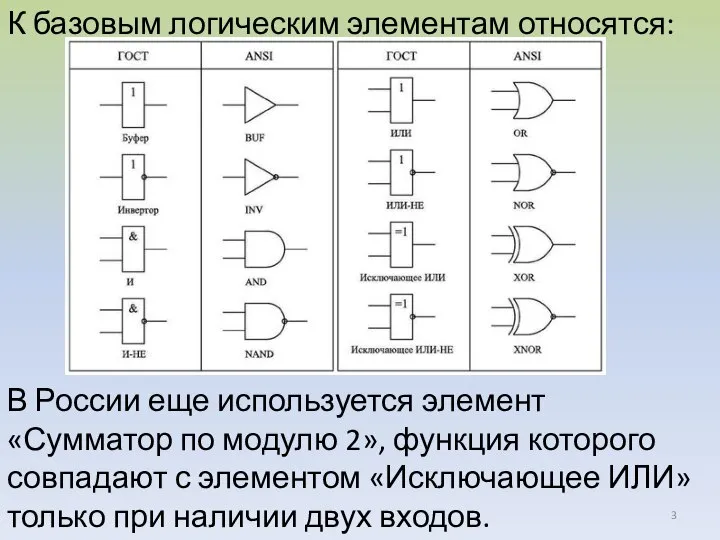
- 3. К базовым логическим элементам относятся: В России еще используется элемент «Сумматор по модулю 2», функция которого
- 4. При построении функциональных схем используется совокупность типовых логических элементов, образующих функционально полную систему (базис). Основными базисами
- 5. Способы кодирования логических сигналов В связи с использованием двухзначной логики в логических схемах как входные, так
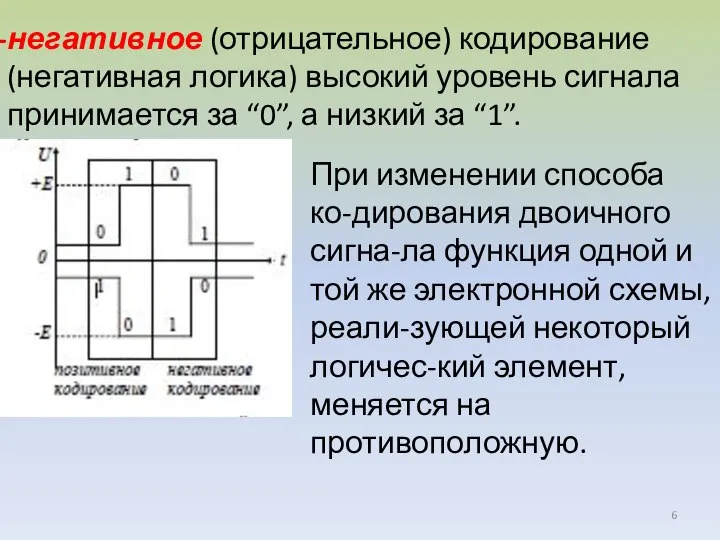
- 6. негативное (отрицательное) кодирование (негативная логика) высокий уровень сигнала принимается за “0”, а низкий за “1”. При
- 7. Понятие логической схемы. Типы логических схем Функциональная логическая схема представляет собой совокупность логических элементов и связей
- 8. В реальных электронных схемах подача логичес-кой константы на вход элемента реализуется заземлением или подключением этого входа,
- 9. В комбинационных схемах значение выходного сигнала в любой момент времени зависит только от комбинации входных сигналов
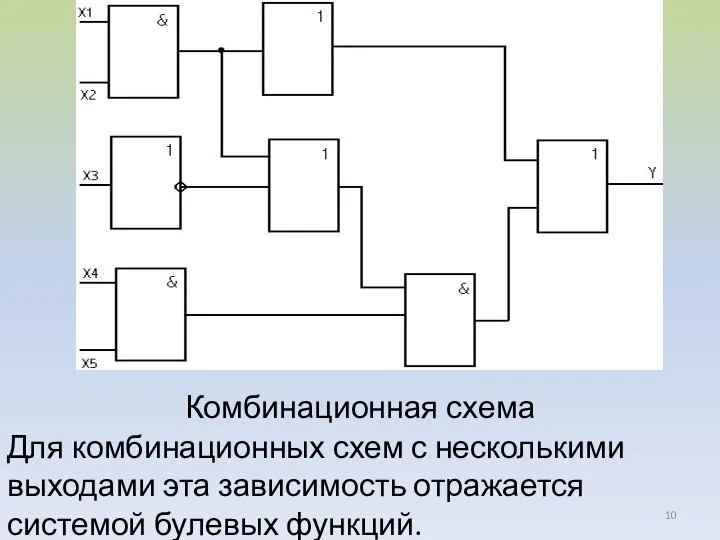
- 10. + Комбинационная схема Для комбинационных схем с несколькими выходами эта зависимость отражается системой булевых функций.
- 11. В последовательностных схемах значение вы-ходного сигнала в любой момент времени зависит не только от комбинации входных
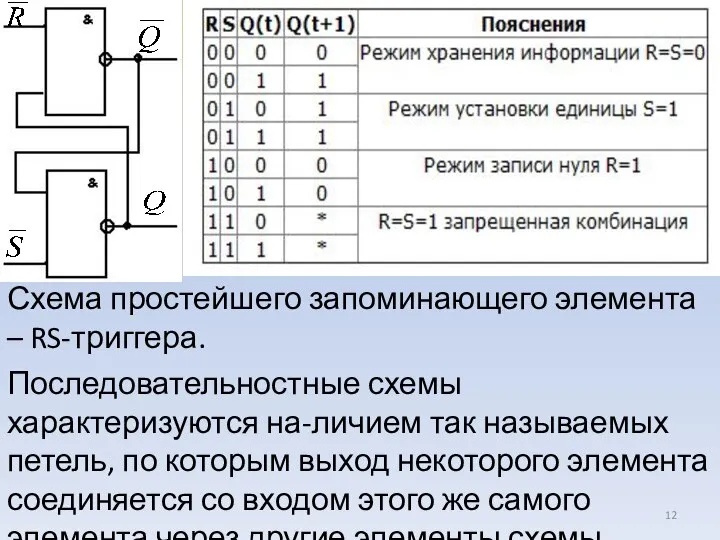
- 12. Схема простейшего запоминающего элемента – RS-триггера. Последовательностные схемы характеризуются на-личием так называемых петель, по которым выход
- 13. Основные параметры комбинационных схем Основными параметрами комбинационных схем (КС) является стоимость и быстродействие. Стоимость КС определяется
- 14. Быстродействие схемы, как правило, оценивает-ся задержкой распространения сигналов от входов схемы к ее выходу. Для абстрактных
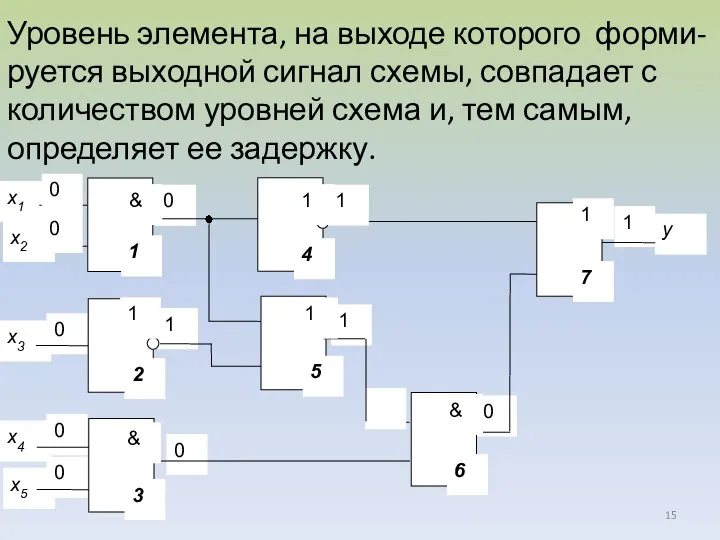
- 15. Уровень элемента, на выходе которого форми-руется выходной сигнал схемы, совпадает с количеством уровней схема и, тем
- 16. Для схемы, приведенной на рисунке: - элементы 1,2,3 относятся к первому уровню; - элементы 4,5 ко
- 17. Для определения функции схемы целесообразно использовать метод подстановки. Его идея сос-тоит в следующем. Выходы логических элементов
- 18. Полученное выражение для функции у можно привести к ДНФ и далее упростить с использова-нием законов булевой
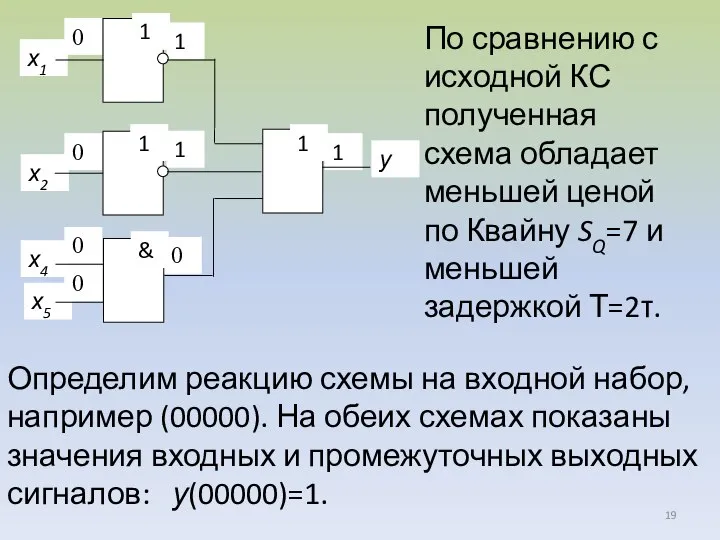
- 19. По сравнению с исходной КС полученная схема обладает меньшей ценой по Квайну SQ=7 и меньшей задержкой
- 20. Задача синтеза состоит в построении комбинационной схемы по заданному закону функционирования. При решении задачи синтеза необходимо
- 21. Естественно, что используемая система элементов должна обладать свойством функциональной пол-ноты, то есть быть достаточной для построения
- 22. В тех случаях, когда критерием эффективности схемы является цена по Квайну, над минимальны-ми формами проводят дополнительные
- 23. Пример подобной постановки задачи синтеза: син-тезировать схему с минимальной ценой по Квайну и с задержкой, не
- 24. При интегральной реализации регистров в целях минимизации числа выходов интегральной микросхемы выходные сигналы регистров, как правило,
- 25. - коэффициент объединения по входу, который представляет собой ограничение на число входов в логический элемент и
- 26. В связи с этим при построении схем в реальной системе элементов необходимо минимизировать не столько число
- 27. 7. В реальных системах элементов, как правило, используется значительное разнообразие логических элементов, относящихся к разным базисам.
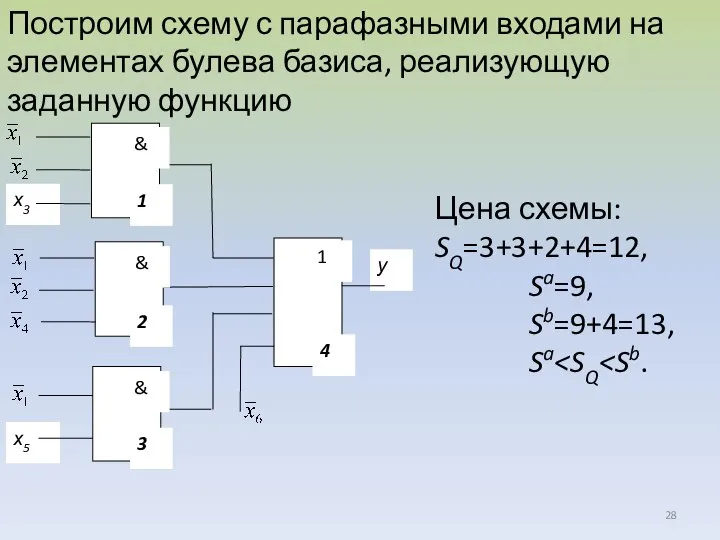
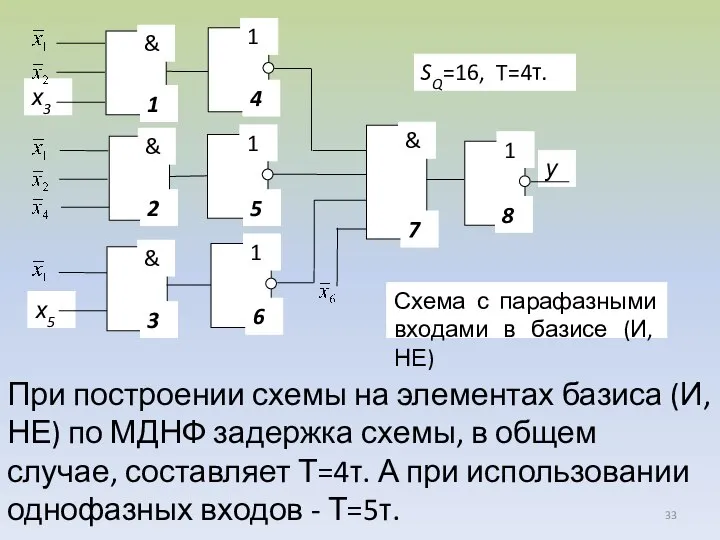
- 28. Построим схему с парафазными входами на элементах булева базиса, реализующую заданную функцию Цена схемы: SQ=3+3+2+4=12, Sa=9,
- 29. В общем случае, задержка схемы с парафазными входами: Т=2τ (схема двухуровневая), в частном случае Т=1τ. При
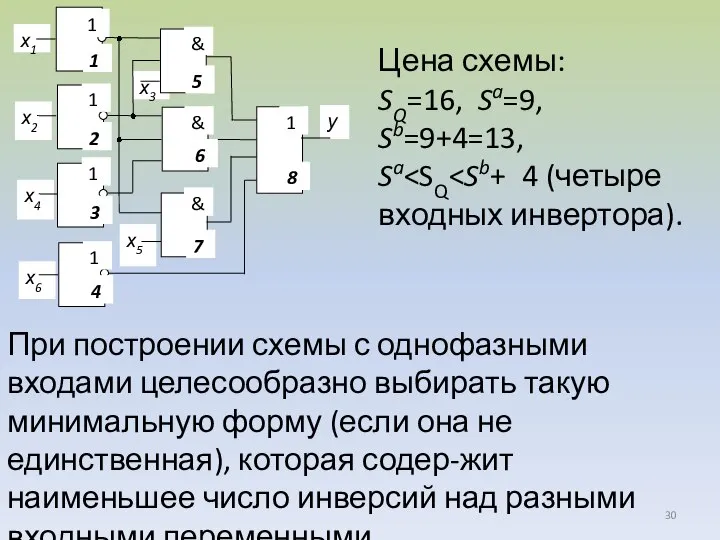
- 30. Цена схемы: SQ=16, Sa=9, Sb=9+4=13, Sa При построении схемы с однофазными входами целесообразно выбирать такую минимальную
- 31. При наличии единственной минимальной нор-мальной формы, можно осуществить ее преобра-зование с использованием законов двойного отрицания и
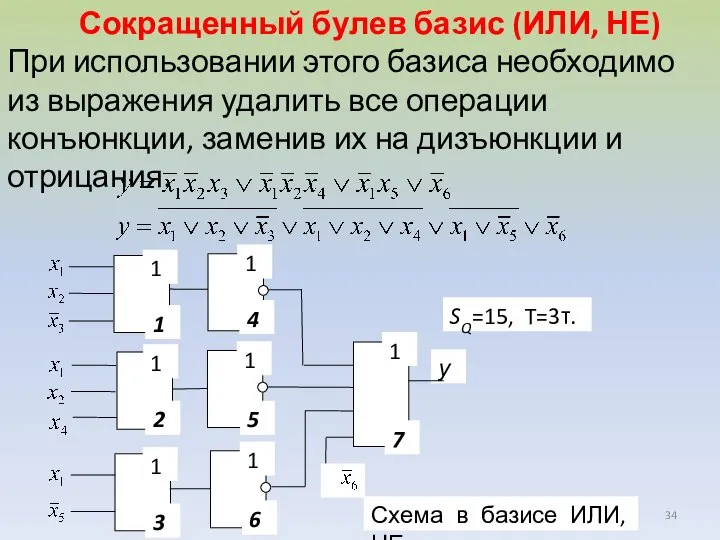
- 32. Сокращенный булев базис (И, НЕ) При использовании этого базиса необходимо из используемого выражения удалить все операции
- 33. При построении схемы на элементах базиса (И, НЕ) по МДНФ задержка схемы, в общем случае, составляет
- 34. Сокращенный булев базис (ИЛИ, НЕ) При использовании этого базиса необходимо из выражения удалить все операции конъюнкции,
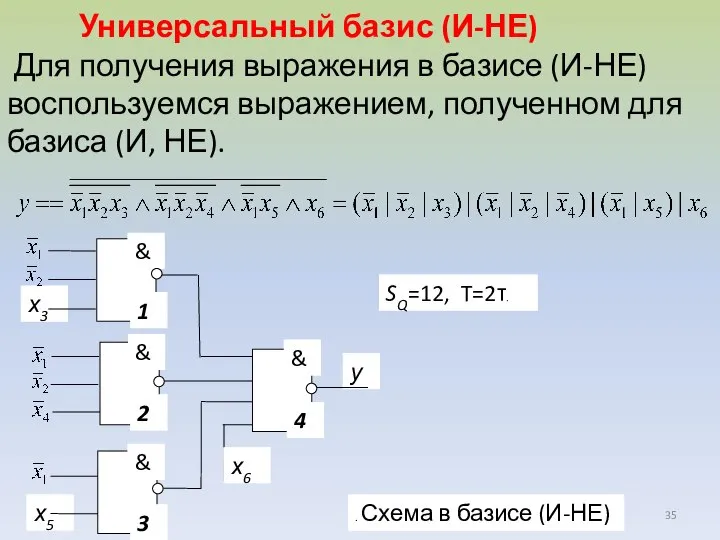
- 35. Универсальный базис (И-НЕ) Для получения выражения в базисе (И-НЕ) воспользуемся выражением, полученном для базиса (И, НЕ).
- 36. Заметим, что цена по Квайну и задержка схемы, построенной в базисе (И-НЕ), такие же, как и
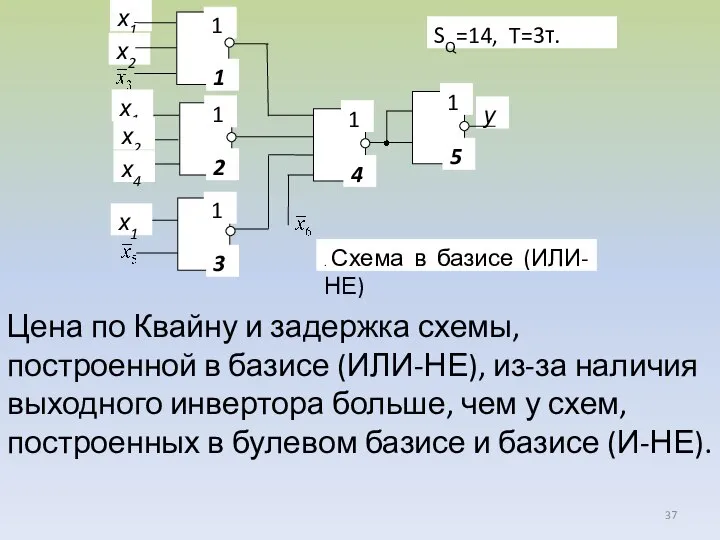
- 37. Цена по Квайну и задержка схемы, построенной в базисе (ИЛИ-НЕ), из-за наличия выходного инвертора больше, чем
- 38. Рассмотрим факторное преобразование булевой функции из примера вынесем из первых двух термов переменные получим Задача факторизации
- 39. можно из исходного выражения сначала из трех термов вынести переменную а затем из первых двух термов
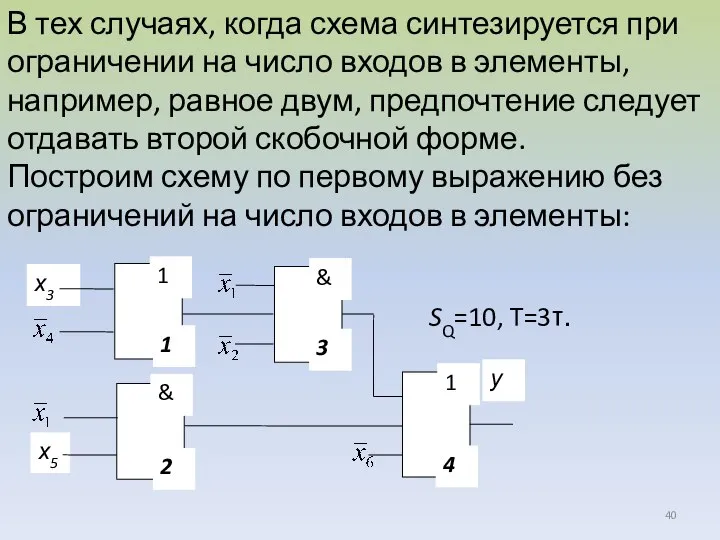
- 40. В тех случаях, когда схема синтезируется при ограничении на число входов в элементы, например, равное двум,
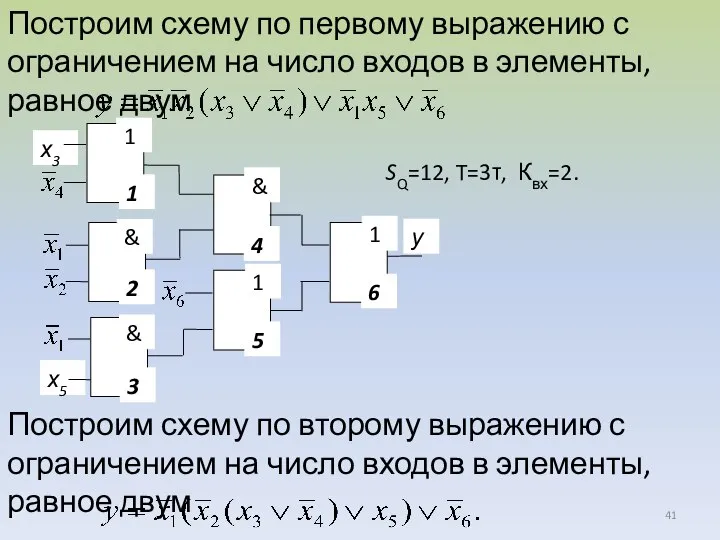
- 41. Построим схему по первому выражению с ограничением на число входов в элементы, равное двум SQ=12, T=3τ,
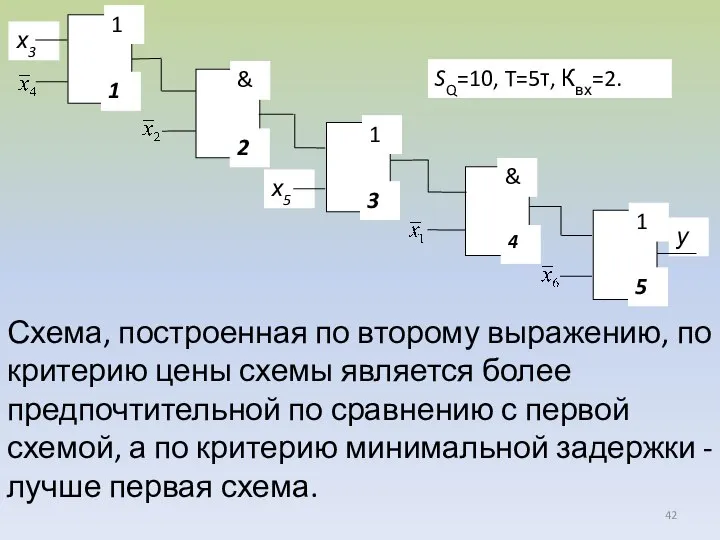
- 42. Схема, построенная по второму выражению, по критерию цены схемы является более предпочтительной по сравнению с первой
- 43. Пример. Для функции, заданной в МКНФ выполним факторное преобразование. Вынесем из первых двух термов дизъюнкцию можно
- 44. Оценка эффекта факторизации Этот эффект характеризуется разностью цен схемы до и после факторизации. Можно показать, что
- 45. Замечание. Для эффективного решения задачи факторизации необходимо учитывать следующее: 1. При наличии у булевой функции нескольких
- 46. d d d 1 1 1 Второе покрытие не минимальное, но эффект от факторизации больше. 3.
- 47. Пример. Выполним факторизацию булевой функции, заданной в МДНФ y= x1x2x3 ∨ x1x2x4 ∨ x1x3x5x6 ∨ x2x4x5x6=
- 48. Декомпозиция булевых функций Задача декомпозиции булевой функции в общем случае состоит в таком разделении множества ее
- 49. Пример. Рассмотрим задачу декомпозиции функции от трех переменных: . Заметим, что минимальные формы функции совпадают с
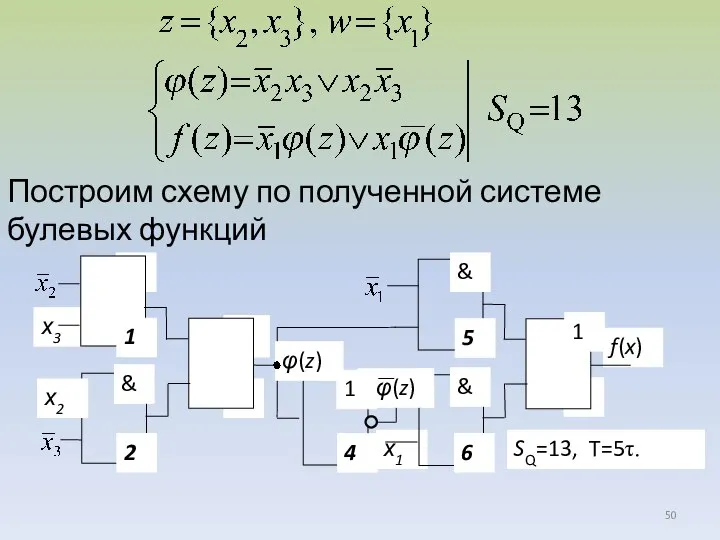
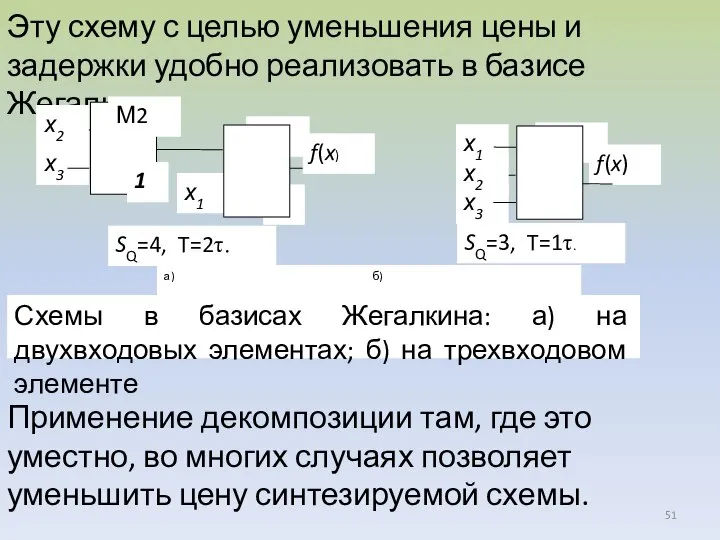
- 50. Построим схему по полученной системе булевых функций
- 51. Эту схему с целью уменьшения цены и задержки удобно реализовать в базисе Жегалкина Применение декомпозиции там,
- 52. Пример. Применить факторизацию и декомпозицию к функции Вынесем из трех последних термов переменную Применим к функции
- 53. Синтез многовыходных комбинационных схем Многовыходная комбинационная схема (МКС) представляется в виде обобщенного «черного ящика», а закон
- 54. При решении задачи синтеза МКС применяются методы минимизации, факторизации и, возможно, декомпозиции, только не к одной
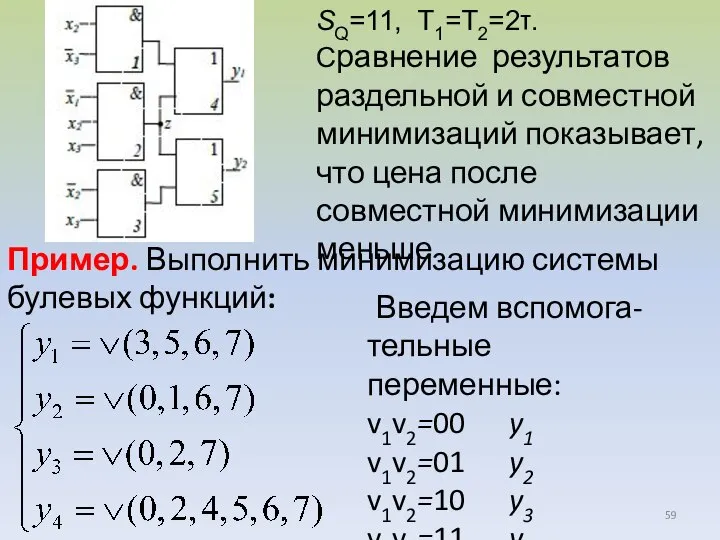
- 55. Пример. Решим задачу минимизации системы булевых функций: Раздельная минимизация функций системы Решим задачу минимизации раздельно для
- 56. При построении комбинационной схемы по МДНФ, она распадается на две независимые подсхемы, отдельные для реализаций каждой
- 57. Совместная минимизация функций системы Решим задачу минимизации совместно для обеих функций системы. Приведем систему булевых функций
- 58. Минимальное покрытие состоит из трех кубов, первый из которых принадлежит только функции y2, второй – y1,
- 59. SQ=11, T1=T2=2τ. Сравнение результатов раздельной и совместной минимизаций показывает, что цена после совместной минимизации меньше Пример.
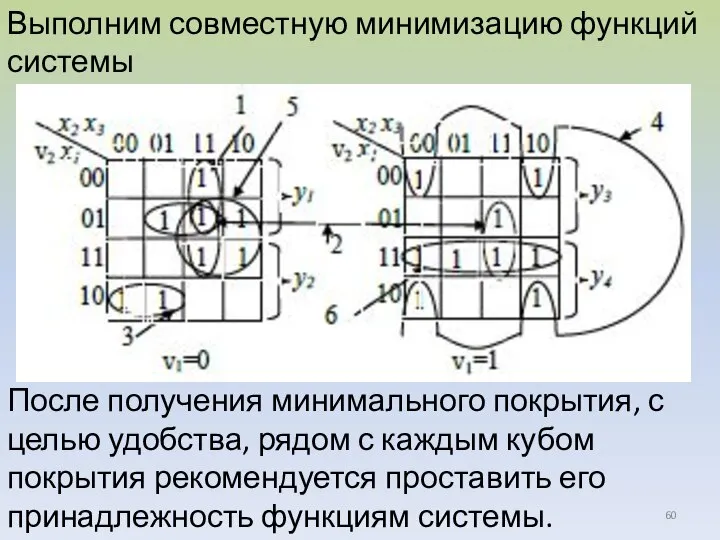
- 60. Выполним совместную минимизацию функций системы После получения минимального покрытия, с целью удобства, рядом с каждым кубом
- 62. При совместной минимизации булевых функций может оказаться, что некоторые кубы поглощаются другими, т.е. после получения минимальной
- 65. При введении вспомогательных переменных следует учитывать, что кодирование функций системы влияет на результат минимизации. И для
- 66. Далее выписываются минимальные формы для отдельных функций с учетом их собственных термов и общих термов, принадлежащих
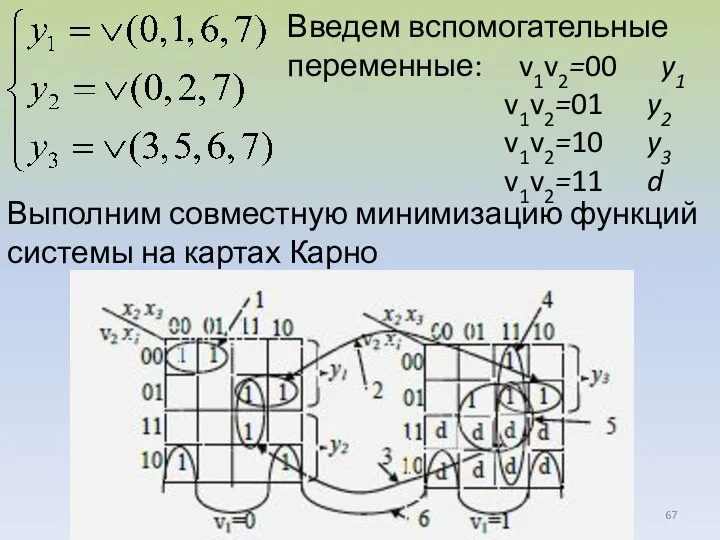
- 67. Введем вспомогательные переменные: v1v2=00 y1 v1v2=01 y2 v1v2=10 y3 v1v2=11 d Выполним совместную минимизацию функций системы
- 68. Общие термы: Заметим, что третий куб, на самом деле, соответствует простым импликантам только для функций y1
- 69. Замечание. Для большого числа функций от многих аргументов применение карт Карно для совместной минимизации выглядит затруднительным.
- 70. Факторизация системы булевых функций Применительно к системе булевых функций задача факторизации состоит в выделении общих термов
- 71. Пример. Выполним факторизацию системы булевых функций: Введем общий терм z: Особенно актуальной задача факторизации становится при
- 72. Эффект факторизации системы булевых функций – нулевой. Проведем раздельную факторизацию:
- 73. В результате раздельной факторизации цена схемы уменьшилась на два. Эффект возник в результате того, что в
- 75. Замечание. Порядок проведения двух видов факторизации совместной и раздельной в большинстве случаев безразличен. Декомпозиция системы булевых
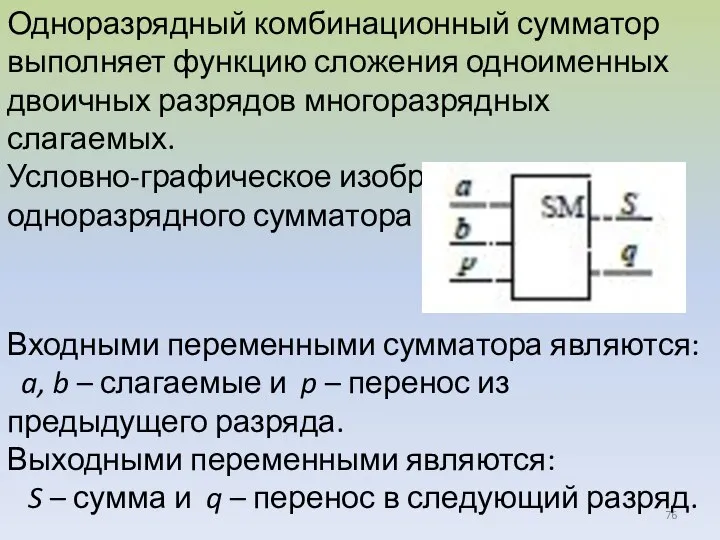
- 76. Одноразрядный комбинационный сумматор выполняет функцию сложения одноименных двоичных разрядов многоразрядных слагаемых. Условно-графическое изображение одноразрядного сумматора Входными
- 77. Закон функционирования одноразрядного сумма-тора представляется в виде следующей системы булевых функций: В соответствии с принципами двоичного
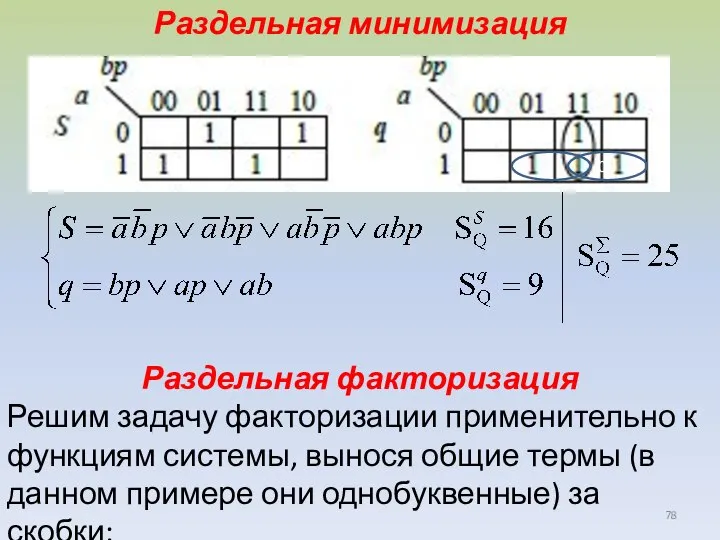
- 78. Раздельная минимизация Раздельная факторизация Решим задачу факторизации применительно к функциям системы, вынося общие термы (в данном
- 79. За счет раздельной факторизации цена схемы, реализующей функцию переноса – q, уменьшилась на единицу, а цена
- 80. Обозначим первую скобку в скобочной форме функции S вспомогательной переменной z. С учетом того, что вторая
- 81. Нетрудно заметить, что в полученной системе функций имеются: во-первых, общий член ab для вспомогательной функции z
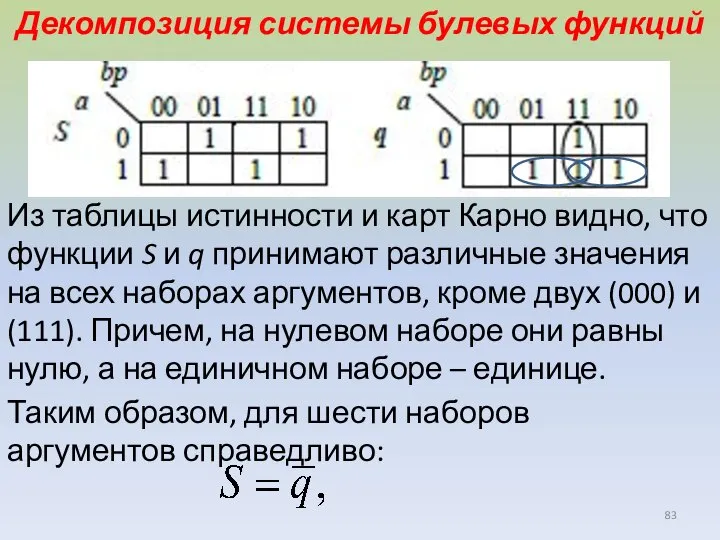
- 83. Декомпозиция системы булевых функций Из таблицы истинности и карт Карно видно, что функции S и q
- 84. то есть можно выразить более сложную по схемной реализации функцию S через более простую по реализации
- 85. Для остальных наборов аргументов конституена a∨b∨p будет равна единице и, следовательно, что справедливо для всех оставшихся
- 86. Выполним совместную факторизацию функций системы:
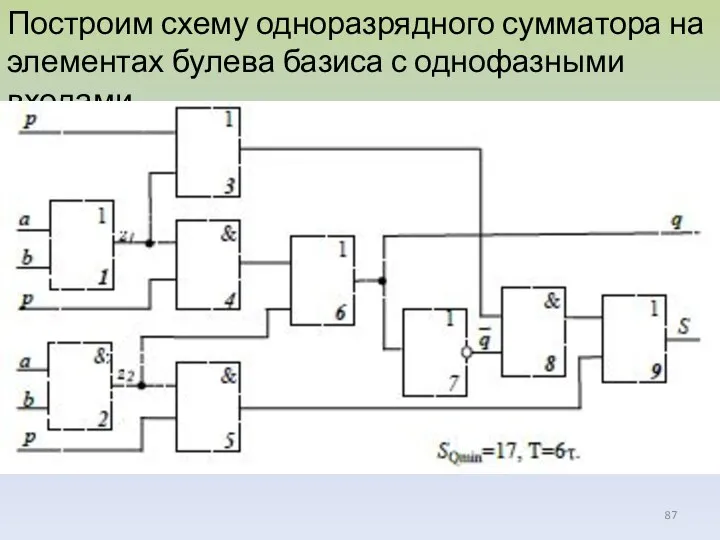
- 87. Построим схему одноразрядного сумматора на элементах булева базиса с однофазными входами
- 88. Сформулируем общие принципы декомпозиции применительно к двум функциям y1 и y2, входящим в некоторую систему функций.
- 89. 2. За исходную функцию из двух следует выбирать ту, которая обладает меньшей ценой схемной реализации (в
- 90. 5. Для исправления исходного равенства на значе-ние y1 = 1 для наборов аргументов Х1 производится дизъюнктивное
- 92. Скачать презентацию











































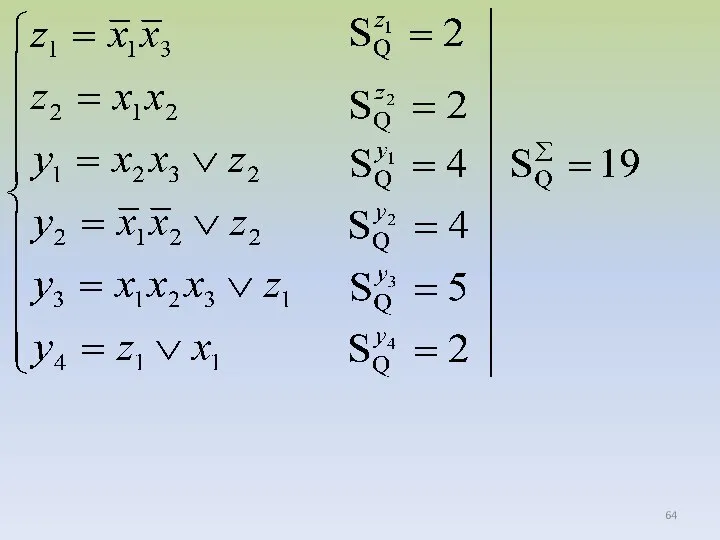








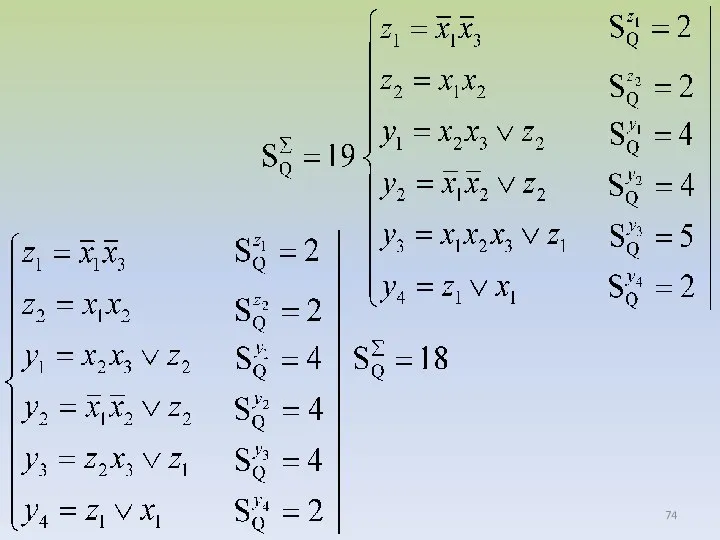





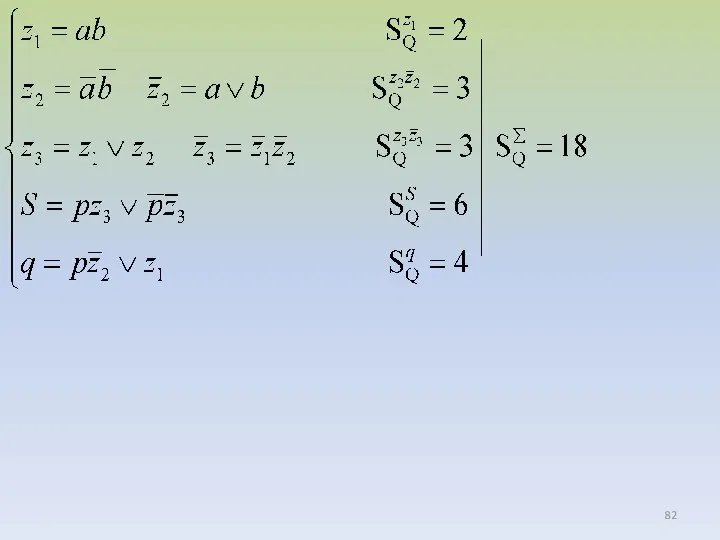






 Классификация программного обеспечения
Классификация программного обеспечения Центральная городская публичная библиотека им. В.В. Маяковского в Санкт-Петербурге
Центральная городская публичная библиотека им. В.В. Маяковского в Санкт-Петербурге Курсовая работа на тему: В стране выученных уроков
Курсовая работа на тему: В стране выученных уроков Компьютерные презентации
Компьютерные презентации Dream Pad — блокнот сновидений в твоём сматфоне
Dream Pad — блокнот сновидений в твоём сматфоне Комплектующие компьютера
Комплектующие компьютера Основная схема воздействия в социальной инженерии. Лекция 3
Основная схема воздействия в социальной инженерии. Лекция 3 Базы данных
Базы данных Информационный портал Будущее России. Национальные проекты
Информационный портал Будущее России. Национальные проекты Ручное тестирование ПО. Классы эквивалентности и граничные условия. Планирование и работа с требованиями
Ручное тестирование ПО. Классы эквивалентности и граничные условия. Планирование и работа с требованиями Выбор жизненного цикла ИТ-проекта. Лекция 3
Выбор жизненного цикла ИТ-проекта. Лекция 3 Біоінформатика. Бази даних. Модель NCBI. Lab.1
Біоінформатика. Бази даних. Модель NCBI. Lab.1 Pencil Code. Подфункции и тестирование
Pencil Code. Подфункции и тестирование iKnow and DeepSee. Agenda
iKnow and DeepSee. Agenda Молодежь
Молодежь GNU Эмулятор данные и переходы
GNU Эмулятор данные и переходы Информационная система для профессионального образования Бугульминский машиностроительный техникум
Информационная система для профессионального образования Бугульминский машиностроительный техникум Предпроектная стадия создания информационной системы
Предпроектная стадия создания информационной системы Текстуры
Текстуры Компьютерный вирус
Компьютерный вирус Система поиска книг, фильмов и музыки
Система поиска книг, фильмов и музыки Информатика. Системы счисления. Лекция 3
Информатика. Системы счисления. Лекция 3 Программирование циклических алгоритмов. Начала программирования
Программирование циклических алгоритмов. Начала программирования Подготовка электронных документов
Подготовка электронных документов Информатика. Часть 2
Информатика. Часть 2 Klassenarbeit Kalender und deutsche Feste
Klassenarbeit Kalender und deutsche Feste Какие эмоции сделают контент вирусным
Какие эмоции сделают контент вирусным Алгоритмы с ветвящейся структурой. Программирование ветвлений на Паскале
Алгоритмы с ветвящейся структурой. Программирование ветвлений на Паскале