Содержание
- 2. Системы счисления § 7. Системы счисления § 8. Двоичная система счисления § 9. Восьмеричная система счисления
- 3. Что такое система счисления? Система счисления — это правила записи чисел с помощью специальных знаков —
- 4. Непозиционные системы счисления Непозиционная система счисления — это такая система, в которой значение цифры не зависит
- 5. Египетская десятичная система – 1 – 10 – 100 – 1000 – 10000 – 100000 –
- 6. Римская система счисления I – 1 (палец) V – 5 (раскрытая ладонь) X – 10 (две
- 7. Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только
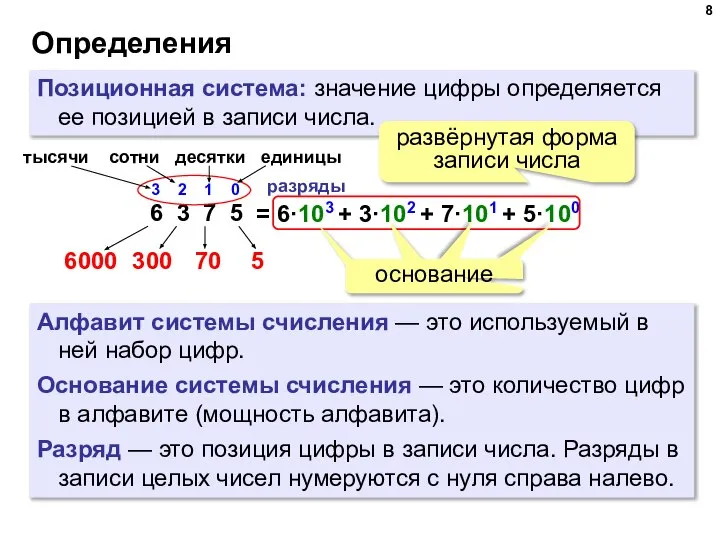
- 8. Определения Позиционная система: значение цифры определяется ее позицией в записи числа. Алфавит системы счисления — это
- 9. Другие позиционные системы двоичная восьмеричная шестнадцатеричная и другие… 101102 = 1⋅24 + 0⋅23 + 1⋅22 +
- 10. Позиционные системы счисления Задача. В некоторой системе счисления число 58 записывается как 46x. Определите основание x
- 11. Системы счисления § 2. Двоичная система счисления
- 12. Двоичная система счисления Основание (количество цифр): 2 Алфавит: 0, 1 длинная запись чисел: 1024 = 100000000002
- 13. Перевод в десятичную систему 2 → 10 100112 4 3 2 1 0 разряды = 1·24
- 14. Выделение степеней числа 2 10 → 2 77 77 = 64 + 13 8 + 5
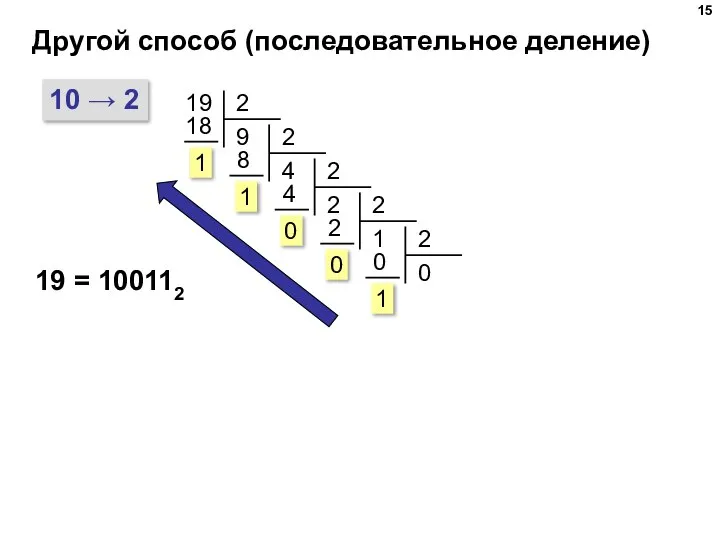
- 15. Другой способ (последовательное деление) 10 → 2 19 19 = 100112
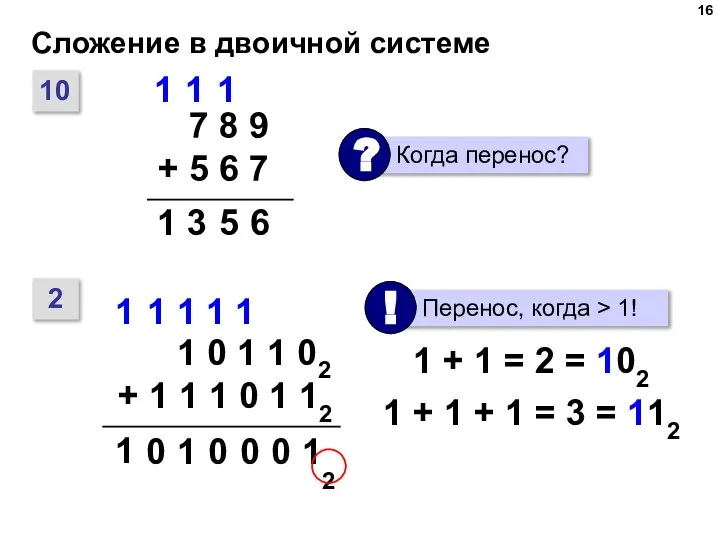
- 16. Сложение в двоичной системе 10 6 5 3 1 1 1 1 2 1 0 1
- 17. Сложение в двоичной системе
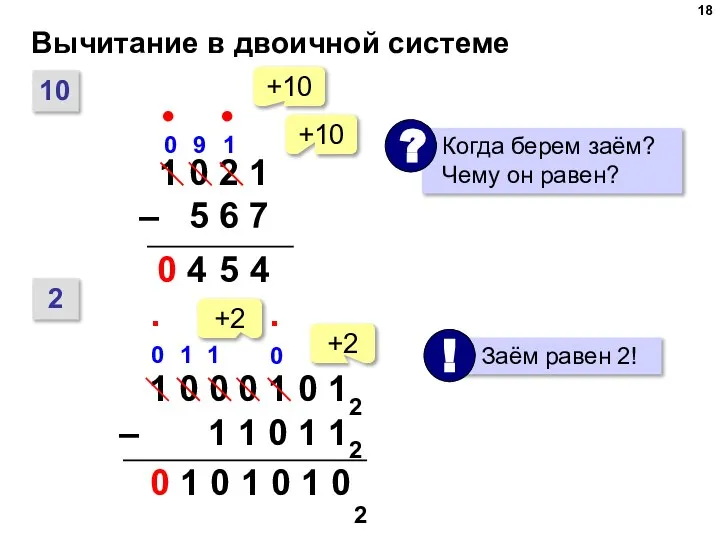
- 18. Вычитание в двоичной системе 10 4 5 4 9 • • 0 2 1 0 +10
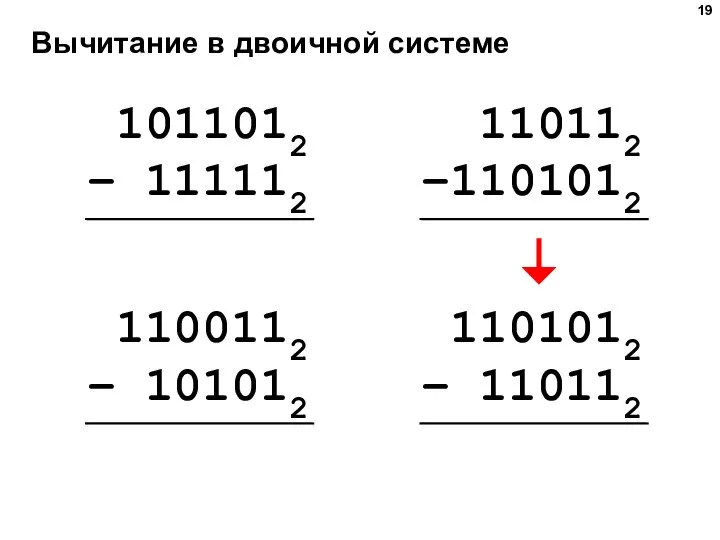
- 19. Вычитание в двоичной системе
- 20. Системы счисления § 3. Восьмеричная система счисления
- 21. Восьмеричная система счисления Основание: 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 32758 69868
- 22. Из восьмеричной в десятичную 8 → 10 1448 2 1 0 разряды = 1·82 + 4·81
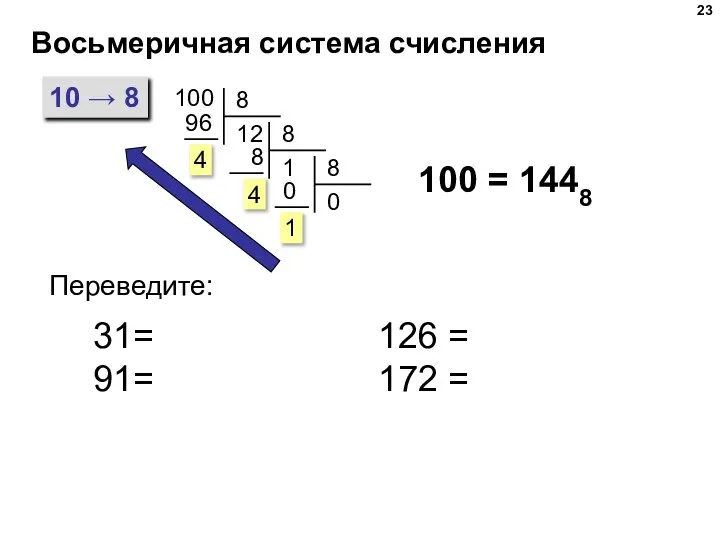
- 23. Восьмеричная система счисления 10 → 8 100 100 = 1448 Переведите: 31= 91= 126 = 172
- 24. Связь с двоичной системой 8 = 23 16258 = 1 6 2 5 001 { {
- 25. Перевод из двоичной в восьмеричную 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011
- 26. Перевести: Переведите в двоичную систему: 3758 = 52468 = Переведите в восьмеричную систему: 10100112 = 101011002
- 27. Системы счисления § 4. Шестнадцатеричная система счисления
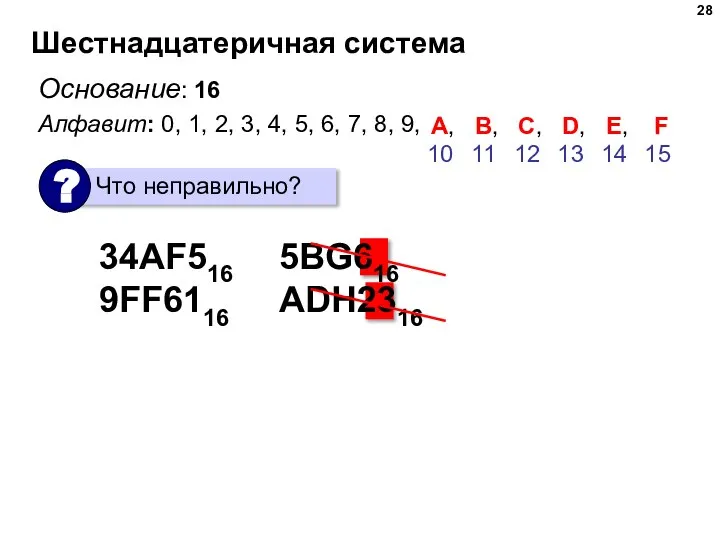
- 28. Шестнадцатеричная система Основание: 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A,
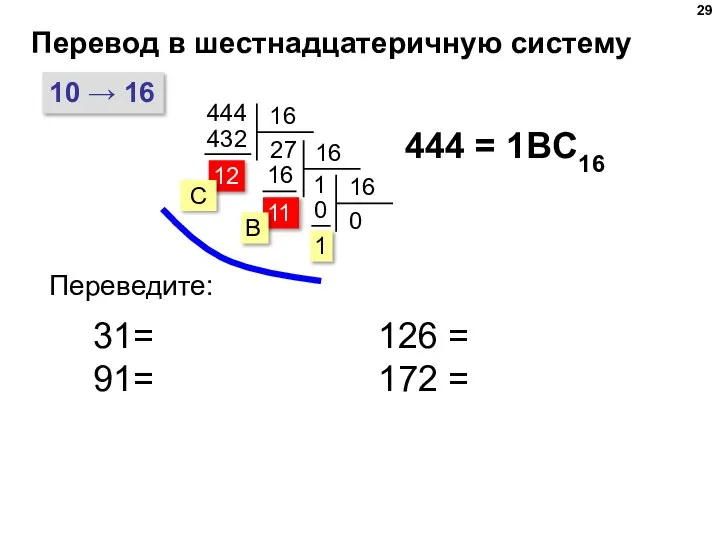
- 29. Перевод в шестнадцатеричную систему 11 10 → 16 444 444 = 1BC16 С B Переведите: 31=
- 30. Перевод из шестнадцатеричной системы 16 → 10 1BC16 2 1 0 разряды = 1·162 + 11·161
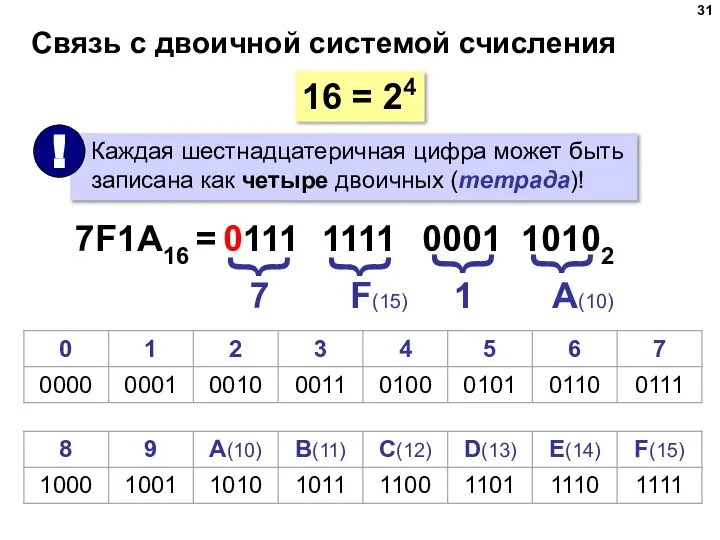
- 31. Связь с двоичной системой счисления 16 = 24 7F1A16 = 7 F(15) 1 A(10) 0111 {
- 32. Перевод из двоичной системы Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112 Шаг
- 34. Скачать презентацию






















 Шаблон презентации на ММСО 2021
Шаблон презентации на ММСО 2021 Доступ к информации и вопросы этики
Доступ к информации и вопросы этики Interacting With Invisible Objects
Interacting With Invisible Objects Исправление документов в текущем периоде
Исправление документов в текущем периоде Компьютерные технологии в спорте
Компьютерные технологии в спорте Опыт взаимодействия с Партнерами в области BIM. Лекция 2
Опыт взаимодействия с Партнерами в области BIM. Лекция 2 TIMELINE for 11 graders
TIMELINE for 11 graders Электронный журнал в Exsel Шаг 1 Рисуем журнал Презентация была создана по просьбе коллег Автор: Сомова С.Г. МБОУ СОШ г. Багратионов
Электронный журнал в Exsel Шаг 1 Рисуем журнал Презентация была создана по просьбе коллег Автор: Сомова С.Г. МБОУ СОШ г. Багратионов Структурированные кабельные системы (СКС)
Структурированные кабельные системы (СКС) Интеллектуальная игра Инфознайка
Интеллектуальная игра Инфознайка Современные персональные компьютеры
Современные персональные компьютеры Интернет-браузеры
Интернет-браузеры С помощью инструментов в программе Paint, построить праздничную открытку
С помощью инструментов в программе Paint, построить праздничную открытку Реализация принципов ООП в .net
Реализация принципов ООП в .net Презентация на тему Операционная система Windows
Презентация на тему Операционная система Windows  Твой друг — учебник. 3 класс
Твой друг — учебник. 3 класс Предмет, методы и система информационного права
Предмет, методы и система информационного права Программное обеспечение по управлению гостиничной системой контроля доступа ADEL. Установка ПО A90 и руководство по эксплуатации
Программное обеспечение по управлению гостиничной системой контроля доступа ADEL. Установка ПО A90 и руководство по эксплуатации Словарь. cnrtl.fr – французский сайт, объединяющий в рамках единого портала набор компьютерных языковых ресурсов
Словарь. cnrtl.fr – французский сайт, объединяющий в рамках единого портала набор компьютерных языковых ресурсов Классы в объектно - ориентированном программировании
Классы в объектно - ориентированном программировании Программирование в среде Scratch
Программирование в среде Scratch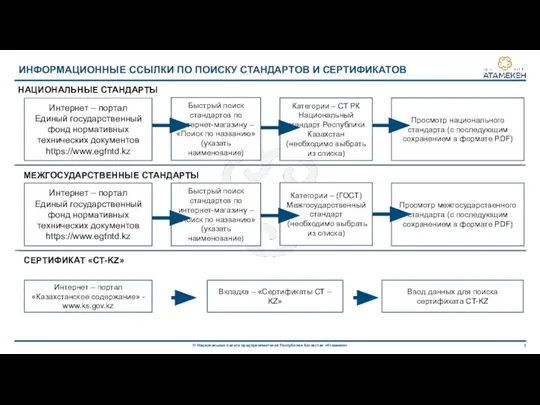 Информационные ссылки по поиску стандартов и сертификатов
Информационные ссылки по поиску стандартов и сертификатов Системы счисления
Системы счисления Разработка катастрофоустойчивых решений для информационных систем персональных данных
Разработка катастрофоустойчивых решений для информационных систем персональных данных Инструкция Grade Master
Инструкция Grade Master Уровни и типы требований
Уровни и типы требований Компьютерный вирус
Компьютерный вирус Диаграммы классов и состояний
Диаграммы классов и состояний