Содержание
- 2. Системы счисления Система счисления (numbering system) - совокупность приемов и правил для записи чисел знаками. Способов
- 3. Непозиционные системы счисления Непозиционная система счисления – система, для которой численное значение символа (цифры) не зависит
- 4. Римская система использует набор следующих символов (цифр): I - "один"; V - "пять"; X - "десять";
- 5. Позиционные системы счисления Позиционная система счисления – система, в которой значение символа (цифры) определяется его положением
- 6. Различные используемые позиционные системы счисления В общем виде для любой позиционной системы счисления с основанием B
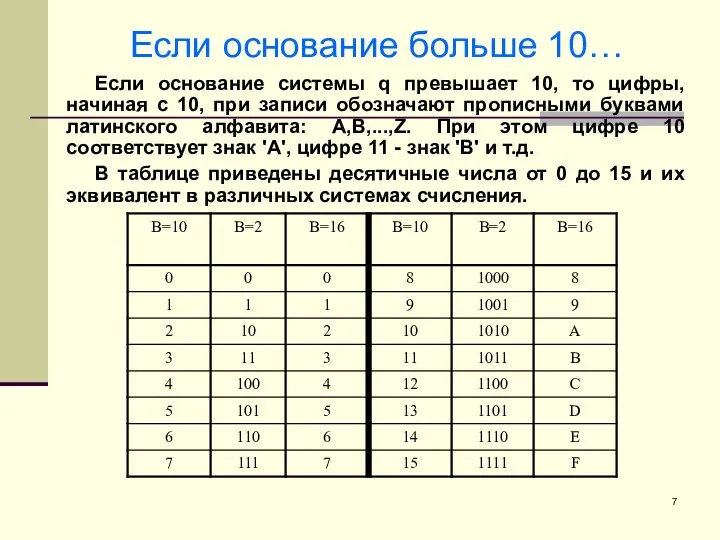
- 7. Если основание больше 10… Если основание системы q превышает 10, то цифры, начиная с 10, при
- 8. Применение различных систем счисления Десятичная (число пальцев на руках) – исторически стала единственной системой, применяемой населением
- 9. Общий метод перевода чисел из одной СС в другую Перевод целых чисел из системы с основанием
- 10. Пример. Перевести десятичное число A = 6110 (q1 = 10) в двоичную систему счисления (q2 =
- 11. Табличный метод перевода В простейшем виде табличный метод заключается в следующем: имеется таблица всех чисел одной
- 12. Пример табличного метода перевода Пример. Перевести десятичное число A = 11310 в двоичную систему счисления, используя
- 13. Какие бывают числа Все эти числа надо каким-то образом представлять в памяти компьютера, выражая их в
- 14. Представление действительных чисел в компьютере Для представления действительных (вещественных) чисел в современных компьютерах принят способ представления
- 15. Представление вещественных чисел в компьютере Примеры: 3,1415926 = 0, 31415926 * 101; 1000=0,1 * 104; 0,123456789
- 16. Представление чисел с плавающей точкой При представлении чисел с плавающей точкой часть разрядов ячейки памяти отводится
- 17. Алгоритм представления числа с плавающей запятой перевести число из P-ичной системы счисления в двоичную; представить двоичное
- 18. Этап 1: Представление числа -25,625 в двоичном виде 0,62510 = 0,1012; -25,62510 = -11001,1012. 2510 =
- 19. Этап 2: Преобразование в экспоненциальную форму: Представление действительного числа не очень удобно изображать в двоичной системе,
- 20. Двоичная арифметика - сложение Пример. Сложить двоичные числа 11012 и 110112. Запишем слагаемые в столбик и
- 21. Таким образом: 1 1 0 1 + 1 1 0 1 1 1 0 1 0
- 22. Двоичная арифметика - вычитание Пример. Вычесть из двоичного числа 1012 двоичное число 112. Запишем алгебраические слагаемые
- 23. Таким образом: 1 0 1 - 1 1 1 0 Для проверки определим десятичные значения слагаемых
- 24. Двоичная арифметика - умножение Пример. Умножить двоичное число 1012 на двоичное число 112. Запишем множители в
- 25. Двоичная арифметика - деление Пример. Разделить двоичное число 11112 на двоичное число 112. Решение задачи представим
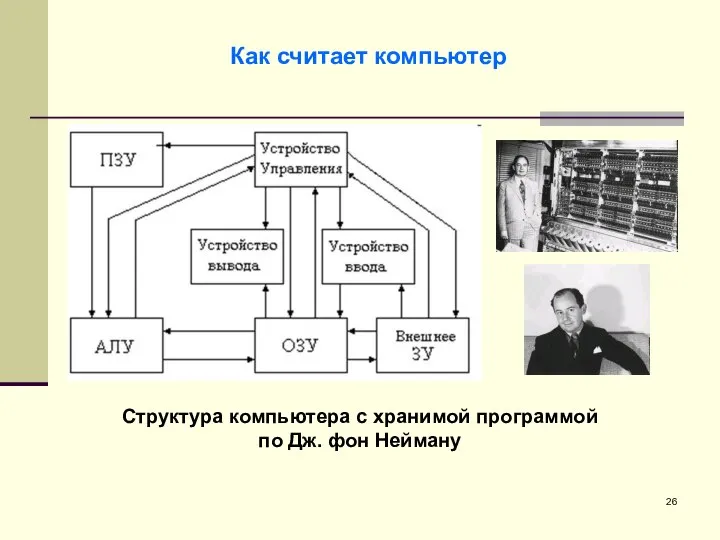
- 26. Как считает компьютер Структура компьютера с хранимой программой по Дж. фон Нейману
- 28. Скачать презентацию























 Продвижение библиотеки в социальных сетях
Продвижение библиотеки в социальных сетях Построение и редактирование геометрических объектов Компас-3D
Построение и редактирование геометрических объектов Компас-3D Приложение STEmnt. Проект
Приложение STEmnt. Проект Презентация на тему Защита информации
Презентация на тему Защита информации  Памятка ДомКлик для клиента
Памятка ДомКлик для клиента Презентация на тему Электронный журнал в Exsel
Презентация на тему Электронный журнал в Exsel  Введение в язык разметки гипертекста HTML
Введение в язык разметки гипертекста HTML Презентация на тему Оперативная память
Презентация на тему Оперативная память 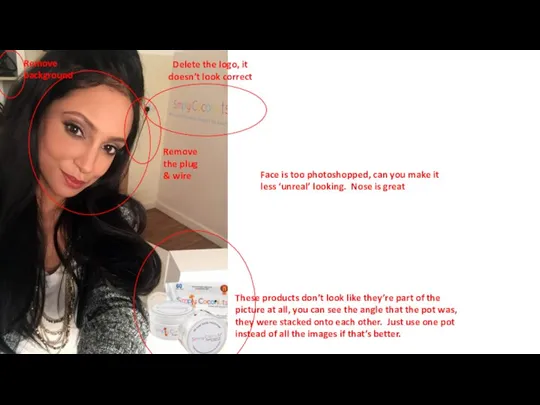 Changes to editorial photо
Changes to editorial photо Хранение информации
Хранение информации RedeX Plus
RedeX Plus Двоичное представление информации в компьютере. Представление чисел в компьютере
Двоичное представление информации в компьютере. Представление чисел в компьютере Алгоритмы. Вопросы
Алгоритмы. Вопросы L3: Apache Spark. Введение
L3: Apache Spark. Введение Крестики-нолики. Графический редактор Paint
Крестики-нолики. Графический редактор Paint Состав компьютера
Состав компьютера Информ_лек2_информатика компьютинг (2)
Информ_лек2_информатика компьютинг (2) СУБД. Способы организации баз данных
СУБД. Способы организации баз данных Шилкина Н.Н., учитель начальных классов, МОУ №1
Шилкина Н.Н., учитель начальных классов, МОУ №1 Интернет-источники по ОРКСЭ
Интернет-источники по ОРКСЭ Бизнес с Китаем. Создание успешного интернет-магазина
Бизнес с Китаем. Создание успешного интернет-магазина CNews Forum
CNews Forum Графические форматы и программная реализация базовых алгоритмов компьютерной графики
Графические форматы и программная реализация базовых алгоритмов компьютерной графики 1156777 (1)
1156777 (1) Как создать страницу компании в Google
Как создать страницу компании в Google Слайды для сайта. Profit max
Слайды для сайта. Profit max Choose the right option
Choose the right option Сервис
Сервис