Слайд 2Что такое сложность вычислений?
Требования к алгоритму:
Быстродействие – временная сложность
Минимальный расход
памяти -

пространственная сложность
Слайд 3Временнáя сложность
T – количество элементарных операций универсального исполнителя (компьютера)
Временная сложность алгоритма –

функция T(n).
Задача 1. Вычислить сумму первых трёх элементов массива (при n ≥ 3).
Sum:= A[1] + A[2] + A[3]
T(n) = 3 (так как 2 сложения + запись в память)
Задача 2. Вычислить сумму всех элементов массива.
Sum:= 0
нц для i от 1 до n
Sum:= Sum + A[i]
кц
T(n) = 2n + 1 (n сложений, n+1 операций записи)
Слайд 4Задача 3. Отсортировать все элементы массива по возрастанию методом выбора.
нц для

i от 1 до n-1
nMin:= i;
нц для j от i+1 до n
если A[i] < A[nMin] то nMin:= j все
кц
если nMin <> i то
c:= A[i]; A[i]:= A[nMin]; A[nMin]:= c
все
кц
Число сравнений:
Число перестановок:
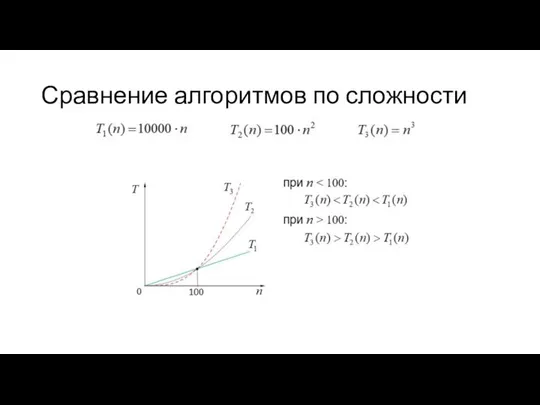
Слайд 5Сравнение алгоритмов по сложности
Слайд 6Асимптотическая сложность
Асимптотическая сложность – это скорость роста количества операций при больших значениях

n.
сложность O(n) ⇔ T(n) ≤ c⋅ n для n ≥ n0
сумма элементов массива:
T(n) = 2⋅ n – 1 ≤ 2⋅ n для n ≥ 1 ⇒ O(n)
сложность O(n2) ⇔ T(n) ≤ c⋅ n2 для n ≥ n0
сортировка методом выбора:
для n ≥ 0 ⇒ O(n2)
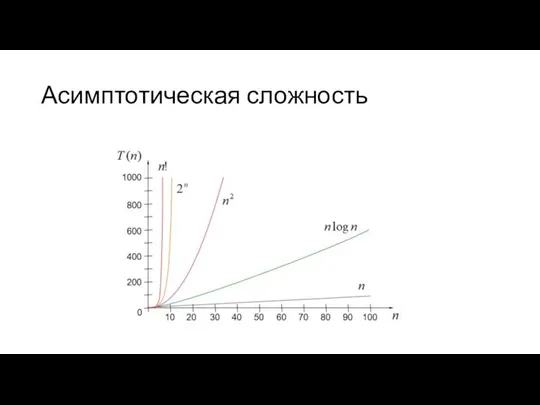
Слайд 7Асимптотическая сложность
сложность O(n3) ⇔ T(n) ≤ c⋅ n3 для n ≥ n0
Алгоритм
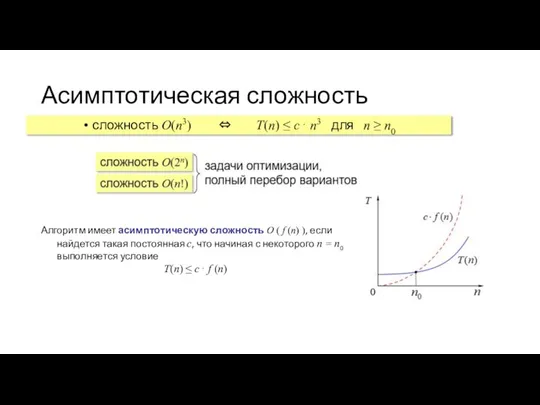
имеет асимптотическую сложность O ( f (n) ), если найдется такая постоянная c, что начиная с некоторого n = n0 выполняется условие
T(n) ≤ c⋅ f (n)
Слайд 9Алгоритмы поиска
Линейный поиск
nX:= 0
нц для i от 1 до n
если

A[i] = X то
nX:= i
выход
все
кц
сложность O(n)
Слайд 10Алгоритмы поиска
Двоичный поиск
L:= 1; R:= n + 1
нц пока L < R

- 1
c:= div(L + R, 2)
если X < A[c] то
R:= c
иначе
L:= c
все
кц
n = 2m шагов T(n) = m + 1
T(n) = log2 n + 1
сложность O(log n) основание логарифма роли не играет
Слайд 11Алгоритмы сортировки
Метод «пузырька»
нц для i от 1 до n-1
нц для j

от n-1 до i шаг -1
если A[j] > A[j+1] то
c:= A[j]; A[j]:= A[j+1]; A[j+1]:= c;
все
кц
кц
сравнений:
присваиваний при перестановках:
сложность O(n2)
Слайд 12Алгоритмы сортировки
Сортировка подсчётом
цел C[1:MAX] Все значения [1,MAX]!
нц для i от 1 до
![Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] Все значения [1,MAX]! нц для i](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1137882/slide-11.jpg)
MAX
C[i]:= 0 обнулить массив счётчиков
кц
нц для i от 1 до n
C[A[i]]:= C[A[i]] + 1 подсчитать, сколько каких чисел
кц
k:= 1
нц для i от 1 до MAX
нц для j от 1 до C[i]
A[k]:= i заполнить массив заново
k:= k + 1 сложность O(n)
кц
кц









![Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] Все значения [1,MAX]! нц для i](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1137882/slide-11.jpg)
 Сервисы для создания контента в соцсетях
Сервисы для создания контента в соцсетях Расширенный поиск в НКРЯ
Расширенный поиск в НКРЯ Исполнитель Робот
Исполнитель Робот Цифровые технологии в строительстве
Цифровые технологии в строительстве Введение в программирование на языке С++
Введение в программирование на языке С++ HTML (HyperText Markup Language, язык разметки гипертекста)
HTML (HyperText Markup Language, язык разметки гипертекста) JavaScript числа
JavaScript числа Интернет-браузеры
Интернет-браузеры Массивы. Понятие массива
Массивы. Понятие массива Шифры
Шифры Компьютерный вирус. Происхождение термина
Компьютерный вирус. Происхождение термина 7-2-3
7-2-3 Visions of Tomorrow
Visions of Tomorrow Подзапросы. Подзапросы в операторах модификации удаления и вставки
Подзапросы. Подзапросы в операторах модификации удаления и вставки Практика в Аpollo-8
Практика в Аpollo-8 Выбор книги в библиотеке. 3 класс
Выбор книги в библиотеке. 3 класс Пирамиды и пирамидальная сортировка
Пирамиды и пирамидальная сортировка Модули в Apache
Модули в Apache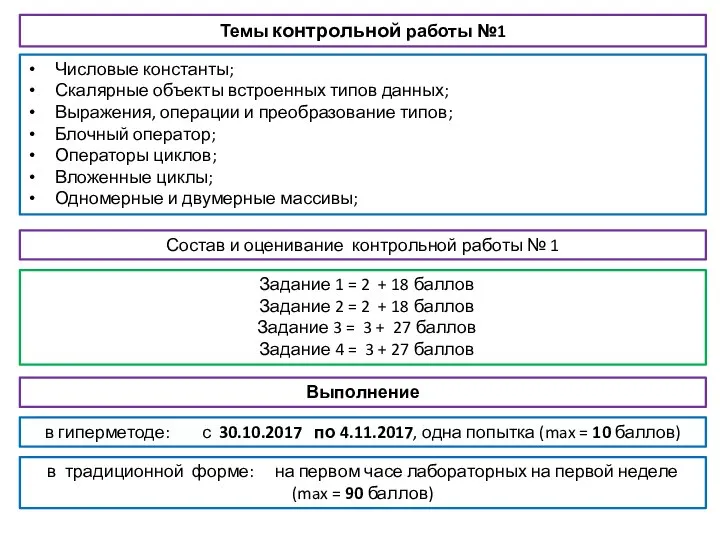 Темы контрольной работы №1
Темы контрольной работы №1 Тема+4.+Встроенный+язык
Тема+4.+Встроенный+язык Алгебра логики
Алгебра логики Часть первая. Основы взаимодействия. Кнопки, текст, картинки
Часть первая. Основы взаимодействия. Кнопки, текст, картинки Создание кроссвордов в Microsoft Office Excel
Создание кроссвордов в Microsoft Office Excel Лекция 4
Лекция 4 Файлы и папки. Имя слайда
Файлы и папки. Имя слайда 15 tcp
15 tcp Klik On — комплексное решение проблем сбыта, логистики, аналитики и автоматизаций бизнес процессов
Klik On — комплексное решение проблем сбыта, логистики, аналитики и автоматизаций бизнес процессов Python Start 1
Python Start 1