Содержание
- 2. При бросании неравносторонней (несимметричной) четырехгранной пирамиды существуют 4 различных события – выпадение каждой из граней с
- 3. В 1948 году американский математик и инженер Клод Шеннон предложил свою формулу вычисления количества информации для
- 4. I = - Σpi⋅log2pi i=1 где I – количество информации, содержащееся в реализации одного из N
- 5. Формулы для частного события с номером i для случая не равновероятных событий : Ni = 2i
- 6. Вероятность i-го события pi выражается в долях единицы и вычисляется по формуле: pi = К /
- 7. Задача 1. В корзине находятся 20 грибов. Из них 15 груздей и 5 волнушек. Какое количество
- 8. Задача 1. В корзине находятся 20 грибов. Из них 15 груздей и 5 волнушек. Какое количество
- 9. Задача 2. В озере обитает 1250 окуней, пескарей – в 2 раза больше, а карасей и
- 10. Задача 3. (работа в парах самостоятельно, затем проверка ответа и разбор решения) В корзине лежат шары:
- 11. Задача 4. (работа в парах самостоятельно, затем проверка ответа и разбор решения) На уроке математики Незнайку
- 13. Скачать презентацию










 ПОКОЛЕНИЯ ЭВМ
ПОКОЛЕНИЯ ЭВМ Игровой интернет-магазин портал “Thrifty gaming”
Игровой интернет-магазин портал “Thrifty gaming” Всеукраїнське друковане інформаційне видання для безкоштовного розповсюдження у поїздах Інтерсіті +, СВ
Всеукраїнське друковане інформаційне видання для безкоштовного розповсюдження у поїздах Інтерсіті +, СВ What’s new in InventorCAM 2015
What’s new in InventorCAM 2015 Программное обеспечение компьютера
Программное обеспечение компьютера 1С: Номенклатура
1С: Номенклатура Experience Financial Companies
Experience Financial Companies Полиморфные вирусы
Полиморфные вирусы Безопасность ребёнка в интернете
Безопасность ребёнка в интернете Виды инфографики
Виды инфографики We need a 3d drawing for cover page of scientific journal
We need a 3d drawing for cover page of scientific journal Бот для назначения совещаний
Бот для назначения совещаний Алгоритмизация и требования к алгоритму. Лекция 1
Алгоритмизация и требования к алгоритму. Лекция 1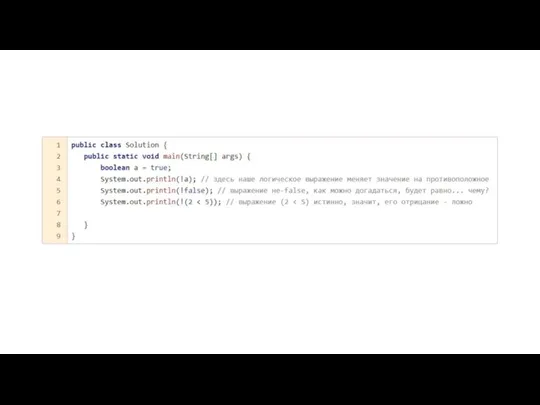 Условный оператор If
Условный оператор If Программирование в среде Robot C. Команды рисования
Программирование в среде Robot C. Команды рисования Безопасность школьников в сети Интернета
Безопасность школьников в сети Интернета Работа с файлами С++/ Многопоточность
Работа с файлами С++/ Многопоточность Постановка целей и задач обработки информации
Постановка целей и задач обработки информации Базы данных
Базы данных Имитация объема в photoshop
Имитация объема в photoshop Создание автоматизированного решебника физических задач в среде MS Excel
Создание автоматизированного решебника физических задач в среде MS Excel Циклы. Занятие 15
Циклы. Занятие 15 Информационные технологиии
Информационные технологиии Информационные технологии. КВН
Информационные технологии. КВН Понятие алгоритма. Виды алгоритмов
Понятие алгоритма. Виды алгоритмов Киберпреступность. Основы проектной деятельности
Киберпреступность. Основы проектной деятельности Антивирусные программы. Урок 8
Антивирусные программы. Урок 8 Количество информации
Количество информации