Анализ экспериментальных данных: компьютерный лабораторный практикум

2.1. Формирование рабочего поля
Подготовим рабочее поле в Excel для выполнения следующих упражнений. Удобно будет,
если мы для текущего задания выделим новый лист книги Excel
1) Внизу слева на рабочем листе таблицы рядом с надписью Лист 1 нажмем на знак + . Рядом появится
Новый лист таблицы Лист 2. Для большей информативности переименуем листы в названия
практических занятий:
Лист 1 → ПЗ 1 Получим вот что
Лист 2 → ПЗ 2
2) Открываем лист ПЗ 2. Нам понадобятся опять два столбца со случайными числами.
Давайте сгенерируем эти столбцы по тем же индивидуальным параметрам, что и на прошлом занятии.
Столбец А с нормальным законом, B – с равномерным. Заодно, закрепим навыки генерации данных.
Чтобы столбцы отличались от предыдущих, при генерации введите в окно Случайное рассеяние
любое целое число. Скажем, 12345
Данные столбцов округлим до десятых
и отсортируем по возрастанию

5) Проверка нормальности выборки по асимметрии и эксцессу
Чтобы ответить на вопрос о том, можно ли признать выборку нормальной, сравнивают выборочные значения
асимметрии и эксцесса (из таблицы описательной статистики) с их ожидаемыми значениями UA и UE .
При N = 500 Ua = 0,109; Ue = 0,21
Вычисляем UA и UE для вашего N, заполняем таблицу, делаем выводы
*Знаки А и Е при сравнении не учитываются, они отражают только направление отклонения параметра.

Вывод: В двух проверенных выборках выпадающих крайних значений не обнаружено

Далее таким же образом, с помощью сокращенных таблиц описательной статистики,
рассчитаем ширины доверительных интервалов для ρ = 99% и 99,9%. Данные сведем в таблицу
Выводы: 1) При повышении уровня доверительной вероятности
ширина доверительного интервала увеличивается
2) Для большинства измерений принято принимать доверительную вероятность
ρ = 95%.
2) Результат измерения любой величины должен быть представлен тремя числами,
например: х = 500±50 (ρ = 95%)

Получим такое диалоговое окно
В нашем случае в диалоговое окно вводят:
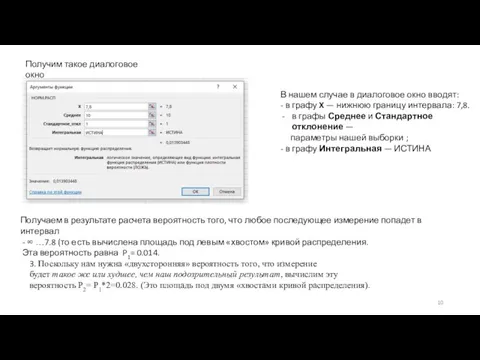
- в графу X — нижнюю границу интервала: 7,8.
в графы Среднее и Стандартное отклонение —
параметры нашей выборки ;
- в графу Интегральная — ИСТИНА
Получаем в результате расчета вероятность того, что любое последующее измерение попадет в интервал
- ∞ …7.8 (то есть вычислена площадь под левым «хвостом» кривой распределения.
Эта вероятность равна P1= 0.014.
3. Поскольку нам нужна «двухсторонняя» вероятность того, что измерение
будет такое же или худшее, чем наш подозрительный результат, вычислим эту
вероятность P2= P1*2=0.028. (Это площадь под двумя «хвостами кривой распределения).

4. Вычисляем величину критерия Шовене, чтобы определить, какова вероятность появления такого же или худшего результата во всей серии из 5 измерений. Эта величина составит P5 = P2*5 = 0.028*5 = 0.14:
5. Поскольку эта величина меньше, чем критериальное значение 0,5, данное подозрительное значение 12, 2 признаем промахом и удаляем его из выборки.
Решаем задачу по отбраковке подозрительного значения
Индивидуальные варианты для решения задачи по применению критерия Шовене приведены ниже в таблице