Technology Mapping

Aug-23
ENEE 644
Outline
What is Technology Mapping?
Technology Mapping Algorithms
Technology Mapping as Graph Covering
Choosing base functions
Creating subject graph
Tree covering problem
Decomposition
Delay Optimization

Aug-23
ENEE 644
Technology Mapping
Technology mapping is the phase of logic synthesis when gates are selected from a technology library to implement the circuit.
Technology mapping is normally done after technology independent optimization.
Why technology mapping?
Straight implementation may not be good. For example, F = abcdef as a 6-input AND gate cause a long delay.
Gates in the library are pre-designed, they are usually optimized in terms of area, delay, power, etc.
Fastest gates along the critical path, area-efficient gates (combination) off the critical path.

Aug-23
ENEE 644
Technology Mapping Algorithms
Basic Requirements:
Provide high quality solutions (circuits).
Adapt to different libraries with minimal effort.
Library may have irregular logic functions.
Support different cost functions.
Transistor count, level count, detailed models for area, delay, and power, etc.
Be efficient in run time.
Two Approaches:
Rule-based techniques
Graph covering techniques (DAG)

Aug-23
ENEE 644
Outline
What is Technology Mapping?
Technology Mapping Algorithms
Technology Mapping as Graph Covering
Choosing base functions
Creating subject graph
Tree covering problem
Decomposition
Delay Optimization

Aug-23
ENEE 644
Base Functions
Base function set is a set of gates which is universal and is used to implement the gates in the technology library.
2-input AND, 2-input OR, and NOT
2-input NAND (and NOT)
Recall: A gate (or a set of gates) is universal if it can implement all the Boolean functions, or equivalently, it can implement 2-input AND, 2-input OR, and NOT.
Choose of base functions:
Universal: able to implement any functions.
Optimal: implement functions efficiently.
Introduce redundant gates: 2-input NAND and NOT.

Aug-23
ENEE 644
Subject Graph
Subject graph is the graph representation of a logic function using only gates from a given base function set. (I.e., the nodes are restricted to base functions.).
For a given base function set, subject graph for a gate may not be unique.
NAND(a,b,c,d) =NAND(NOT(NAND(a,b)),NOT(NAND(c,d))) =NAND(a,NOT(NAND(b,NOT(NAND(c,d)))))
All distinct subject graphs of the same logic have to be considered to obtain global optimal design.

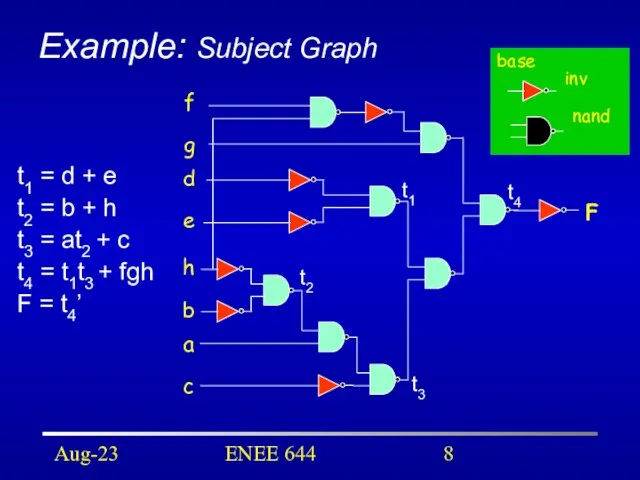
Aug-23
ENEE 644
Example: Subject Graph
t1 = d + e
t2 = b + h
t3 = at2 + c
t4 = t1t3 + fgh
F = t4’
t1
t2
t3
t4
inv
nand
base

Aug-23
ENEE 644
Pattern Graph
For any library gate, its logic function can be represented by a graph where each node is one of the base functions. This graph is called a pattern graph for this library gate.
A pattern graph is a subject graph when the function represents a library gate.
Similarly, all pattern graphs for the same library gate have to be considered.
Tip on choosing base function set: Choose those that provide a small set of pattern graphs.

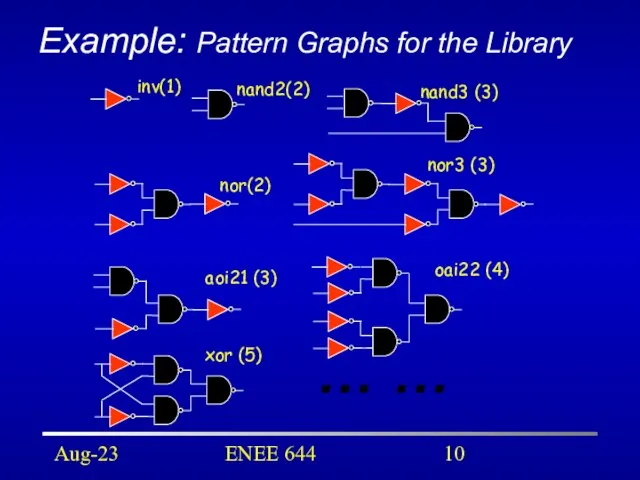
Aug-23
ENEE 644
Example: Pattern Graphs for the Library
inv(1)
nand3 (3)
oai22 (4)
nor(2)
nor3 (3)
xor (5)
aoi21 (3)
nand2(2)
… …

Aug-23
ENEE 644
Cover
A cover is a collection of pattern graphs so that:
every node of the subject graph is contained in one (or more) pattern graphs
each input required by a pattern graph is actually an output of some other pattern graph (i.e. the inputs of one library gate must be outputs from other gates.)
Cost of a Cover
Area: total area of the library gates used (I.e. gates in the cover).
Delay: total delay along the critical path.
Power: total power dissipation of the cover.

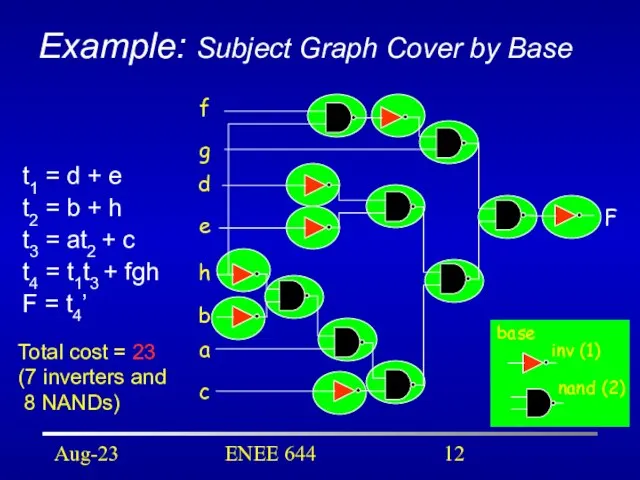
Aug-23
ENEE 644
Example: Subject Graph Cover by Base
F
f
g
d
e
h
b
a
c
Total cost = 23
(7 inverters and
8 NANDs)
t1 = d + e
t2 = b + h
t3 = at2 + c
t4 = t1t3 + fgh
F = t4’
inv (1)
nand (2)
base

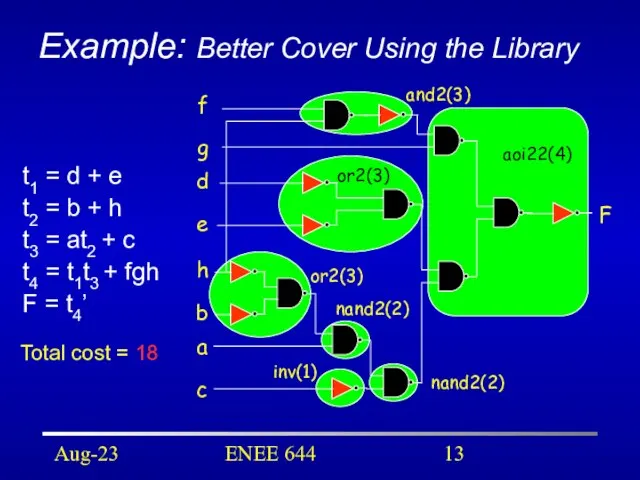
Aug-23
ENEE 644
Example: Better Cover Using the Library
F
f
g
d
e
h
b
a
c
aoi22(4)
and2(3)
or2(3)
or2(3)
Total cost = 18
nand2(2)
nand2(2)
inv(1)
t1 = d + e
t2 = b + h
t3 = at2 + c
t4 = t1t3 + fgh
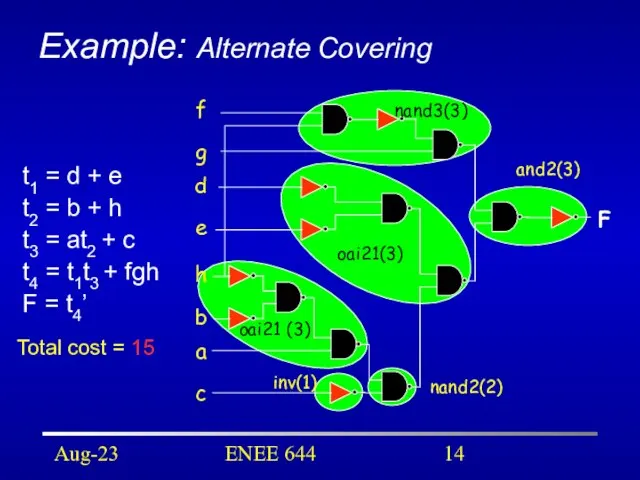
F = t4’

Aug-23
ENEE 644
Example: Alternate Covering
F
f
g
d
e
h
b
a
c
nand3(3)
oai21(3)
oai21 (3)
Total cost = 15
and2(3)
inv(1)
nand2(2)
t1 = d + e
t2 = b + h
t3 = at2 + c
t4 = t1t3 + fgh
F = t4’

Aug-23
ENEE 644
Graph Covering Formation
Technology mapping problem: Find a minimum cost cover of the subject graph by choosing from the collection of pattern graphs for all the gates in the library.
DAG-covering-by-DAG is hard
NP-hard for a simple case:
Only 3 pattern graphs (NOT, 2-input NAND, 2-input NOR)
Each node in the subject graph has no more than 2 fanins and fanouts.
Do We Need to Solve the Problem Optimally?
Input logic from technology-independent optimization
Numerous subject graphs for the same logic network

Aug-23
ENEE 644
Generic Algorithmic Approach
Represent each logic function of the network as a subject graph (DAG);
Generate all possible pattern graphs (DAGs)for each gate in the technology library;
Find an optimal-cost covering of the subject DAG using the collection of pattern DAGs.
Question: how to solve this NP-hard problem?
If subject DAG and pattern DAG’s are trees, an efficient algorithm exists.

Aug-23
ENEE 644
Optimal Tree Covering by Trees
Proposed by Keutzer in program DAGON[DAC’87]
Basic idea: dynamic programming.
Procedure:
Partition the subject graph into trees;
Cover each tree optimally;
Piece the tree-cover into a cover for the subject graph.
Complexity: finding all sub-trees of the subject graph that are isomorphic to a pattern tree. It is linear in the size of subject tree and the size of the pattern trees.

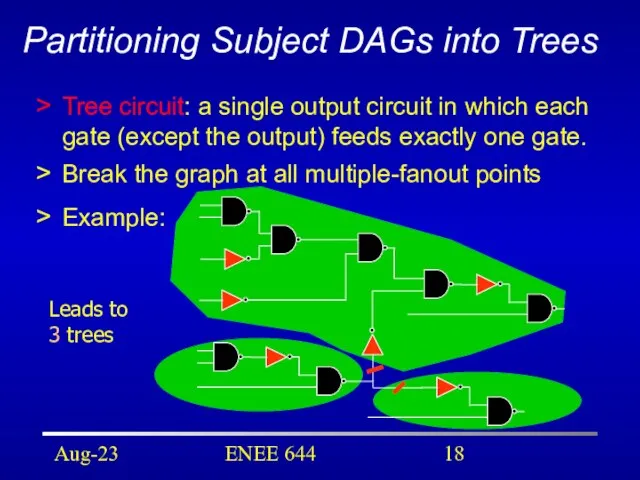
Aug-23
ENEE 644
Partitioning Subject DAGs into Trees
Tree circuit: a single output circuit in which each gate (except the output) feeds exactly one gate.
Break the graph at all multiple-fanout points
Example:

Aug-23
ENEE 644
Tree Covering by Dynamic Programming
For each primary input, cost to cover is 0;
For each (non-leaf) node v in the subject trees (the traverse follows a topological order)
Recursive assumption: we know a best cost cover for each of its (transitive) predecessors.
Recursive formula for cost to cover v:
For each matched pattern graph, compute sum of the cost of this pattern and the total best costs of all fanins to this pattern graph.
Take the minimum as the best cost for node v.
Total cost is the sum of best costs for all primary outputs of the subject trees.

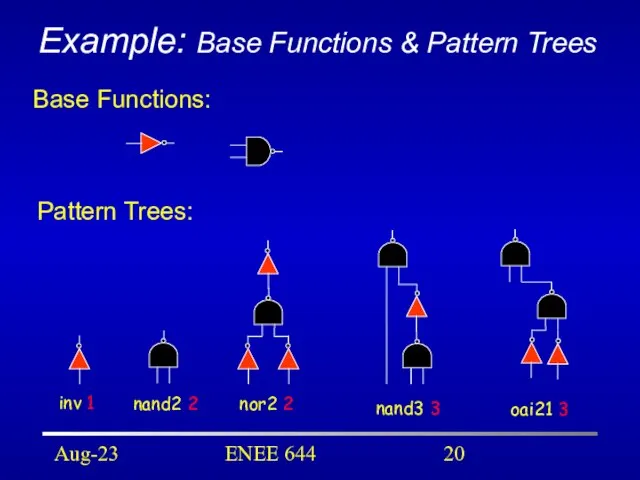
Aug-23
ENEE 644
Example: Base Functions & Pattern Trees
inv 1
nand3 3
oai21 3
nor2 2
nand2 2
Base Functions:
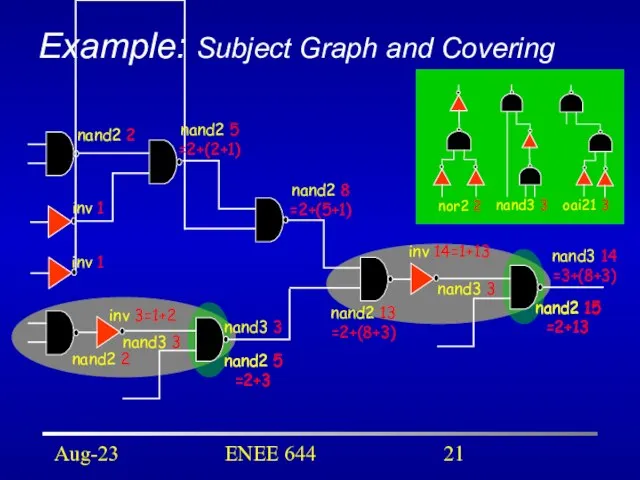
Pattern Trees:

Aug-23
ENEE 644
Example: Subject Graph and Covering
inv 3=1+2
nand2 5
=2+(2+1)
nand2 8
=2+(5+1)
nand3 3
nand2 13
=2+(8+3)
inv 14=1+13
nand3 14
=3+(8+3)

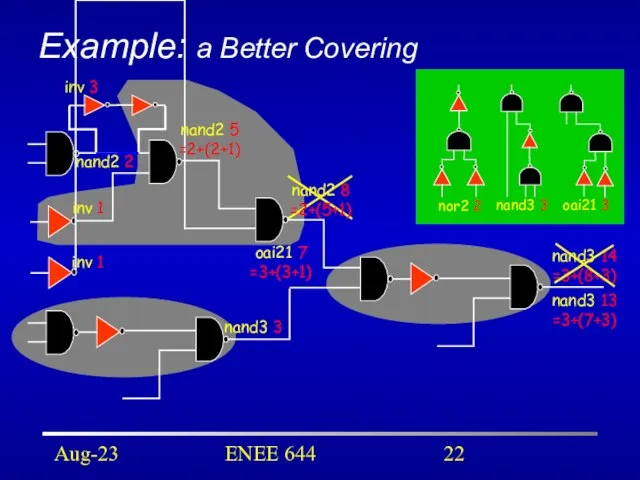
Aug-23
ENEE 644
Example: a Better Covering
nand2 5
=2+(2+1)
nand2 8
=2+(5+1)
nand3 3
nand3 14
=3+(8+3)
nand2 2
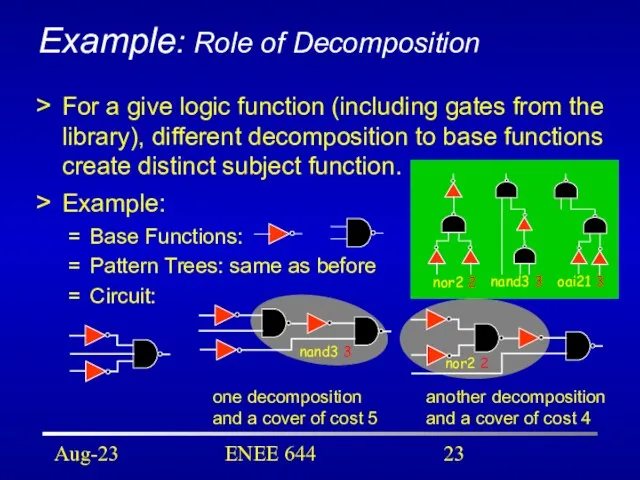
inv 3

Aug-23
ENEE 644
Example: Role of Decomposition
For a give logic function (including gates from the library), different decomposition to base functions create distinct subject function.
Example:
Base Functions:
Pattern Trees: same as before
Circuit:
one decomposition
and a cover of cost 5
another decomposition
and a cover of cost 4
nand3 3
nor2 2

Aug-23
ENEE 644
More on Technology Mapping
Rule-based techniques
DAG covering problem
Tree covering approach
Binate covering problem
Boolean matching
Decomposition + mapping
Technology mapping for performance
Gate resizing after technology mapping
FPGA technology mapping