Слайд 31Влади́мир Алекса́ндрович Коте́льников (24 августа [6 сентябряВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908Влади́мир Алекса́ндрович Коте́льников

(24 августа [6 сентября] 1908, КазаньВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империяВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраляВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005Влади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, МоскваВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, РоссияВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, Россия) — советский и российский учёный в области радиотехники, радиосвязи и радиолокации планетВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, Россия) — советский и российский учёный в области радиотехники, радиосвязи и радиолокации планет, академик Академии наук СССРВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, Россия) — советский и российский учёный в области радиотехники, радиосвязи и радиолокации планет, академик Академии наук СССР (1953) и Российской академии наукВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, Россия) — советский и российский учёный в области радиотехники, радиосвязи и радиолокации планет, академик Академии наук СССР (1953) и Российской академии наук, дважды Герой Социалистического ТрудаВлади́мир Алекса́ндрович Коте́льников (24 августа [6 сентября] 1908, Казань, Российская империя — 11 февраля 2005, Москва, Россия) — советский и российский учёный в области радиотехники, радиосвязи и радиолокации планет, академик Академии наук СССР (1953) и Российской академии наук, дважды Герой Социалистического Труда (1969, 1978), председатель Верховного совета РСФСР (1973—1980). Один из основоположников советской секретной радио- и телефонной связи.




















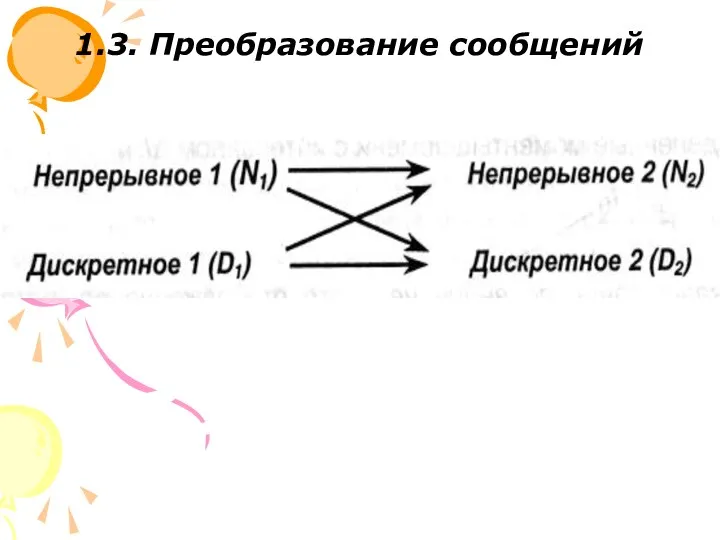



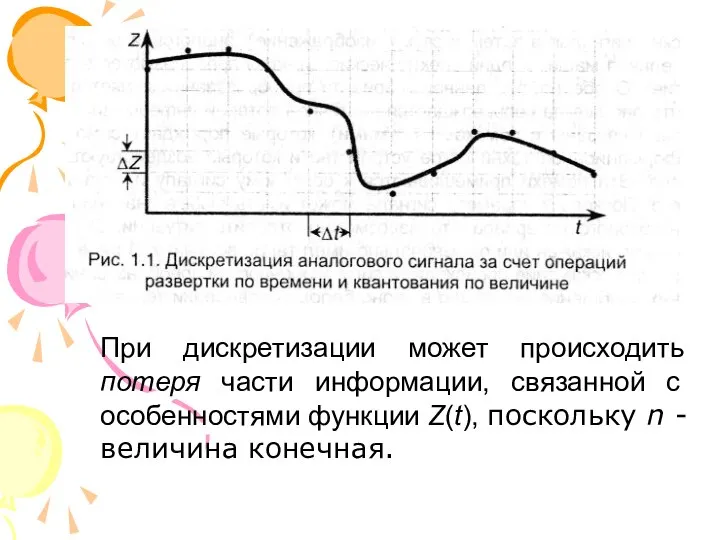


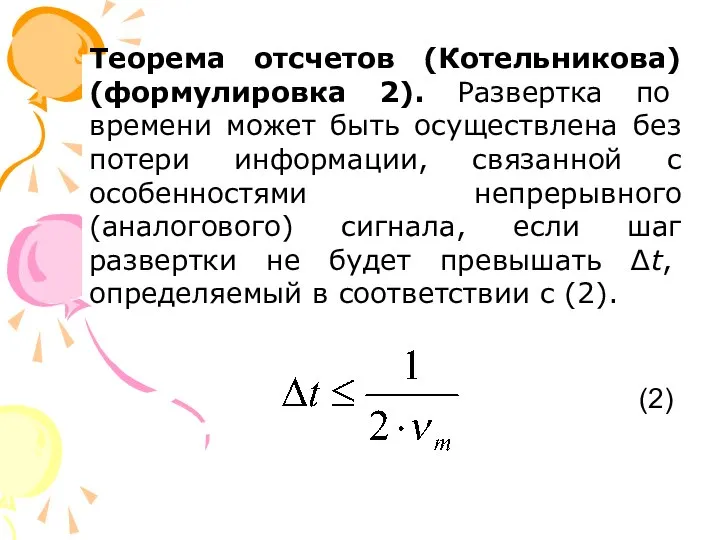

 Хранение информационных объектов различных видов на различных цифровых носителях
Хранение информационных объектов различных видов на различных цифровых носителях Телекомпания НТВ
Телекомпания НТВ Работа в https://learningapps.org
Работа в https://learningapps.org Введение в машинное обучение
Введение в машинное обучение Презентация на тему Что такое информация
Презентация на тему Что такое информация  Бесплатные хостинги
Бесплатные хостинги Создание мультимидийной презентации
Создание мультимидийной презентации Операцiйна система Windows XP
Операцiйна система Windows XP Создание таблицы
Создание таблицы Введение в Python. Лекция 3: Строки и операции над ними
Введение в Python. Лекция 3: Строки и операции над ними Разбор интервью канала BBC NEWS. О чём, с кем и как
Разбор интервью канала BBC NEWS. О чём, с кем и как Тернарный оператор ?:Лекция 25
Тернарный оператор ?:Лекция 25 HTML. Язык описания Web-страниц
HTML. Язык описания Web-страниц Масштабирование изображений с учётом контента
Масштабирование изображений с учётом контента История развития операционной системы Windows
История развития операционной системы Windows FreeMind
FreeMind Помилки в програмі
Помилки в програмі Основные понятия машинного обучения и анализа данных
Основные понятия машинного обучения и анализа данных Команда Создание блока
Команда Создание блока Создание и поддержка единой региональной школьной информационно-библиотечной среды
Создание и поддержка единой региональной школьной информационно-библиотечной среды Проект на тему Сайт ВК
Проект на тему Сайт ВК Компьютерные вирусы
Компьютерные вирусы Таблицы и графы. Задание 1. Информатика в ЕГЭ
Таблицы и графы. Задание 1. Информатика в ЕГЭ ПО для создания интерактивных карт помещений
ПО для создания интерактивных карт помещений Шаблоны День Народного Единства
Шаблоны День Народного Единства Дополнения к проекту
Дополнения к проекту Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Качество программного обеспечения
Качество программного обеспечения