Содержание
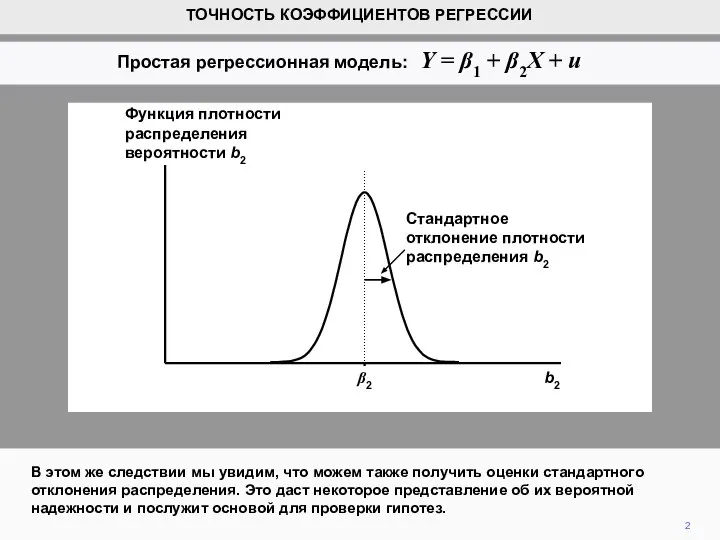
- 2. В этом же следствии мы увидим, что можем также получить оценки стандартного отклонения распределения. Это даст
- 3. Выражения (которые не решены) для дисперсий их распределений показаны выше. См. Вставку 2.3 в тексте для
- 4. Мы сосредоточимся на значении выражения для дисперсии b2. Рассматривая числитель, мы видим, что дисперсия b2 пропорциональна
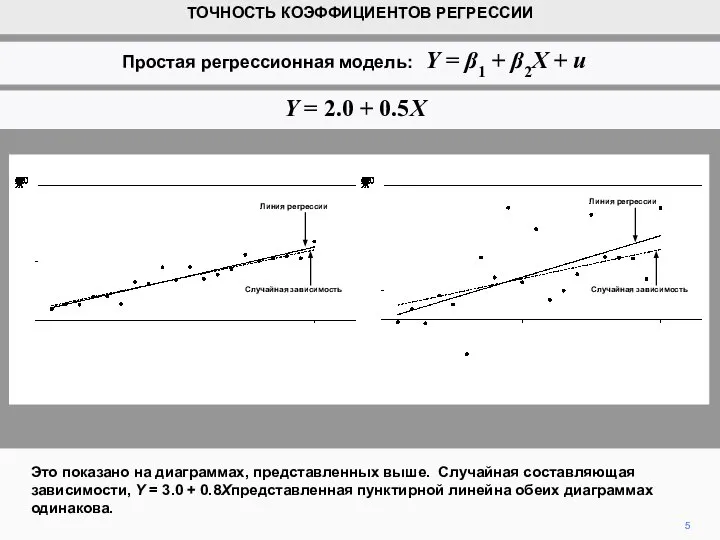
- 5. Это показано на диаграммах, представленных выше. Случайная составляющая зависимости, Y = 3.0 + 0.8Xпредставленная пунктирной линейна
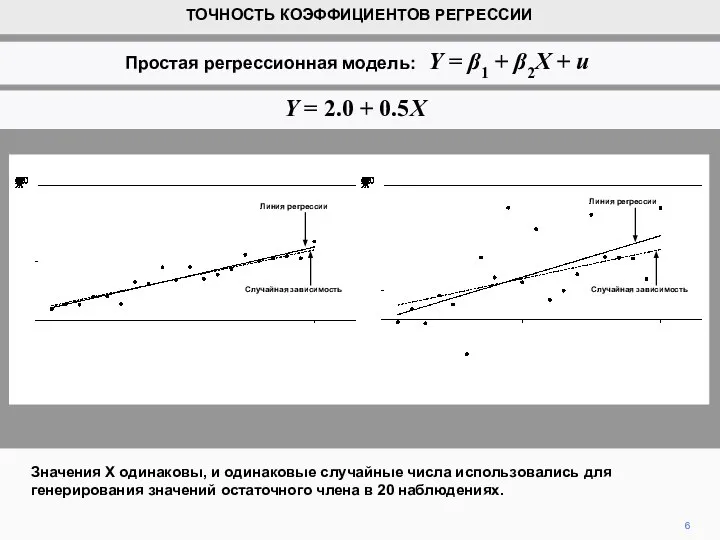
- 6. Значения Х одинаковы, и одинаковые случайные числа использовались для генерирования значений остаточного члена в 20 наблюдениях.
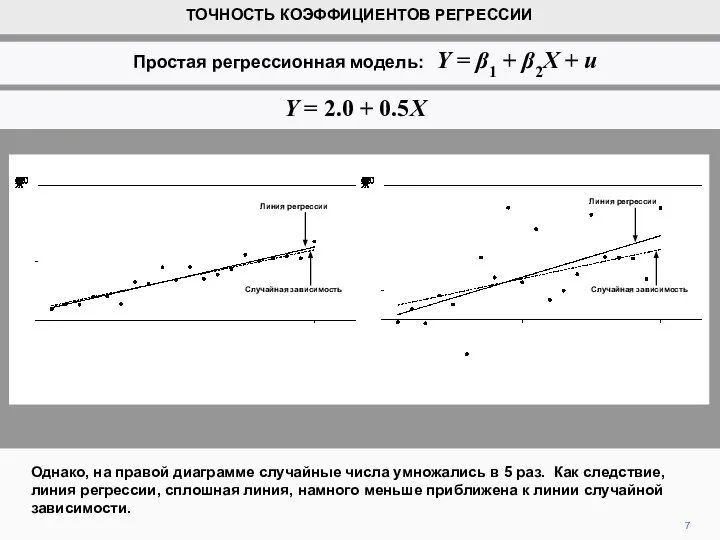
- 7. Однако, на правой диаграмме случайные числа умножались в 5 раз. Как следствие, линия регрессии, сплошная линия,
- 8. Посмотрим на знаменатель выражения для дисперсии b2Чем больше сумма квадратов отклонений X, тем меньше дисперсия b2.
- 9. Однако, значение суммы квадратов отклонений зависит от двух факторов: количества наблюдений и размера отклонений Xi от
- 10. Из приведенного выражения видно, что дисперсия b2 обратно пропорциональна n, числу наблюдений в выборке, которые управляют
- 11. 11 Третьим следствием выражения является то, что дисперсия обратно пропорциональна среднему квадратическому отклонению Х. В чем
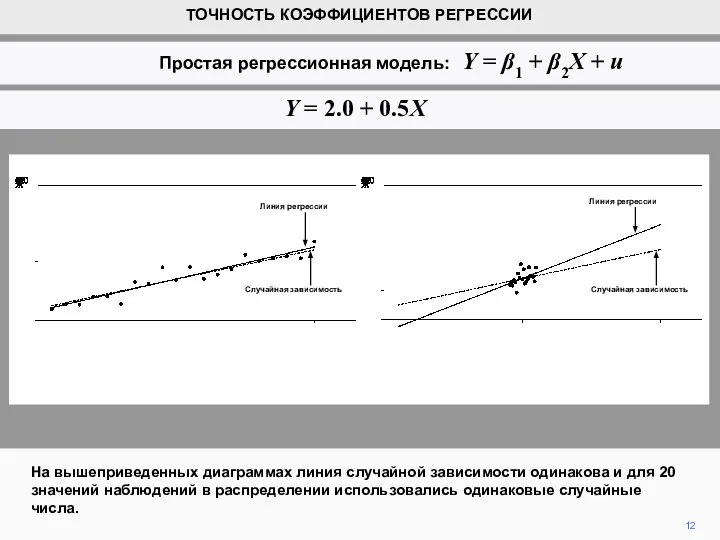
- 12. На вышеприведенных диаграммах линия случайной зависимости одинакова и для 20 значений наблюдений в распределении использовались одинаковые
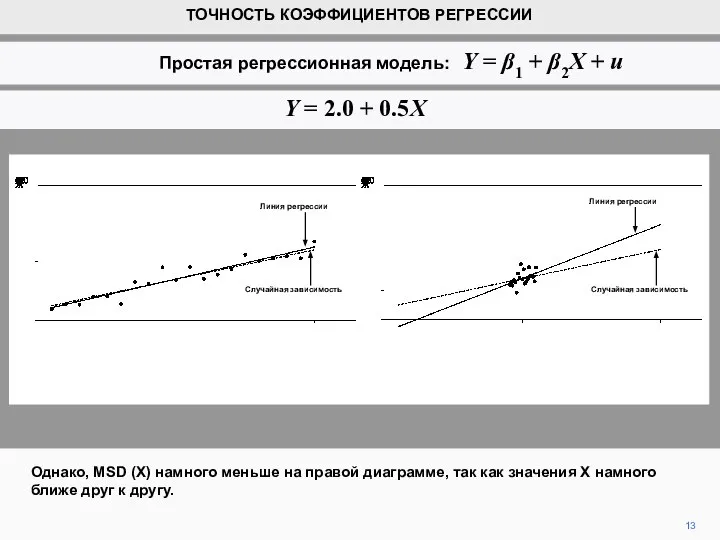
- 13. Однако, MSD (X) намного меньше на правой диаграмме, так как значения Х намного ближе друг к
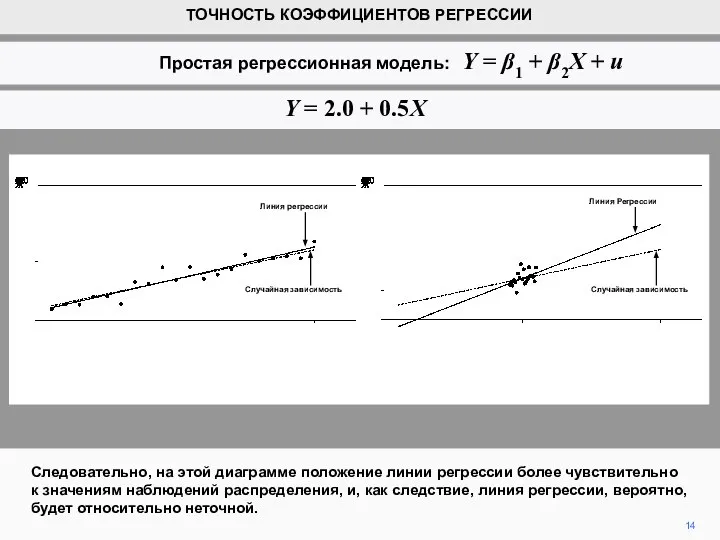
- 14. Следовательно, на этой диаграмме положение линии регрессии более чувствительно к значениям наблюдений распределения, и, как следствие,
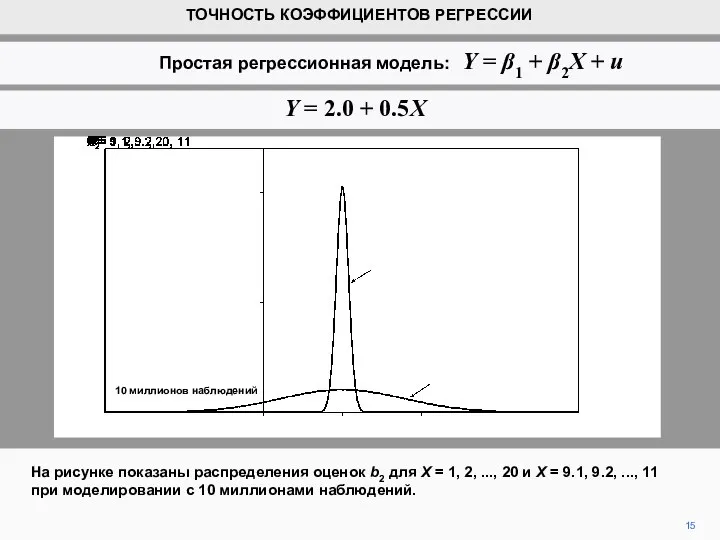
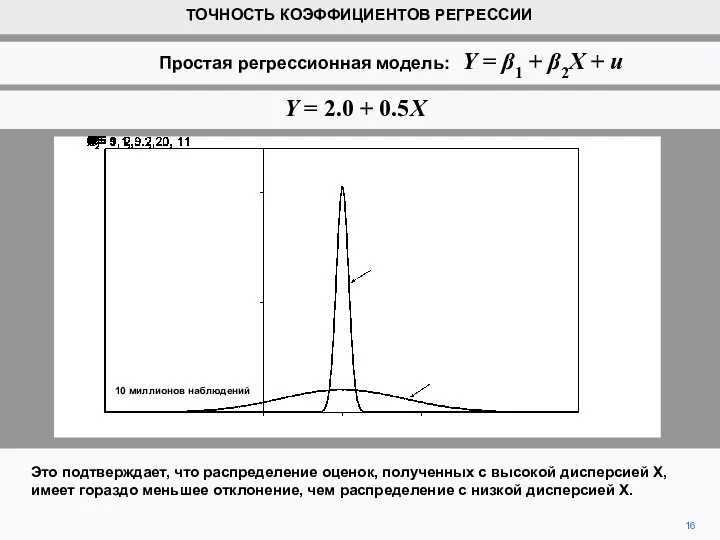
- 15. На рисунке показаны распределения оценок b2 для X = 1, 2, ..., 20 и X =
- 16. Это подтверждает, что распределение оценок, полученных с высокой дисперсией Х, имеет гораздо меньшее отклонение, чем распределение
- 17. Конечно, как видно из выражений дисперсии, отношение MSD (X) к дисперсии u важнее, чем ее абсолютное
- 18. 18 Мы не можем рассчитать теоретические дисперсии именно потому, что не знаем дисперсии остаточного члена. Однако,
- 19. 19 Очевидно, что разброс остатков относительно линии регрессии будет отражать неизвестный разброс u относительно линии Yi
- 20. 20 Одной из мер разброса остатков является их средняя квадратическая ошибка, MSD(e), которая определяется формулой, указанной
- 21. 21 Прежде чем пойти дальше, задайте себе следующий вопрос: какая прямая вероятнее будет ближе к точкам,
- 22. 22 Ответ – линия регрессии, так как по определению она строится таким образом, чтобы свести к
- 23. 23 Следовательно, разброс остатков у нее меньше, чем разброс значений u, а MSD(e) имеет тенденцию занижать
- 24. 24 Действительно, можно показать, что математическое ожидание MSD(e), если имеется всего одна независимая переменная, находится выражением
- 25. 25 Однако отсюда следует, что мы можем получить несмещенную оценку σu2, умножив MSD(e) на n /
- 26. 26 Затем мы можем получить оценки стандартных отклонений распределений b1 и b2, подставив su2 для σu2
- 27. 27 Они описываются как стандартные ошибки b1 и b2, «оценки среднеквадратических отклонений» являются более полными. ТОЧНОСТЬ
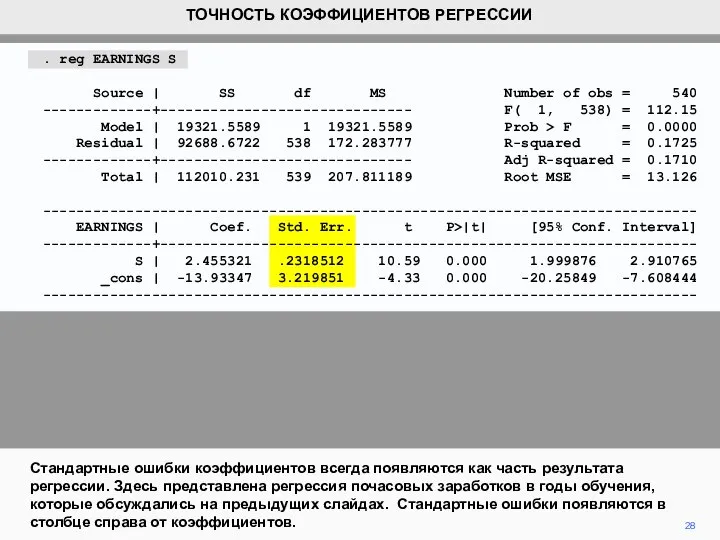
- 28. 28 Стандартные ошибки коэффициентов всегда появляются как часть результата регрессии. Здесь представлена регрессия почасовых заработков в
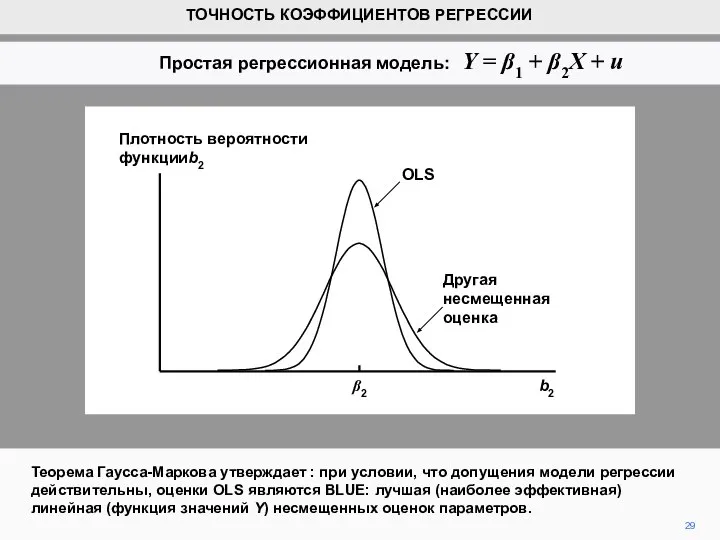
- 29. Теорема Гаусса-Маркова утверждает : при условии, что допущения модели регрессии действительны, оценки OLS являются BLUE: лучшая
- 31. Скачать презентацию

















 Многопоточность
Многопоточность Системы счисления. Логика и алгоритмы. Высказывания, логические операции, кванторы, истинность высказывания
Системы счисления. Логика и алгоритмы. Высказывания, логические операции, кванторы, истинность высказывания Графические форматы и программная реализация базовых алгоритмов компьютерной графики
Графические форматы и программная реализация базовых алгоритмов компьютерной графики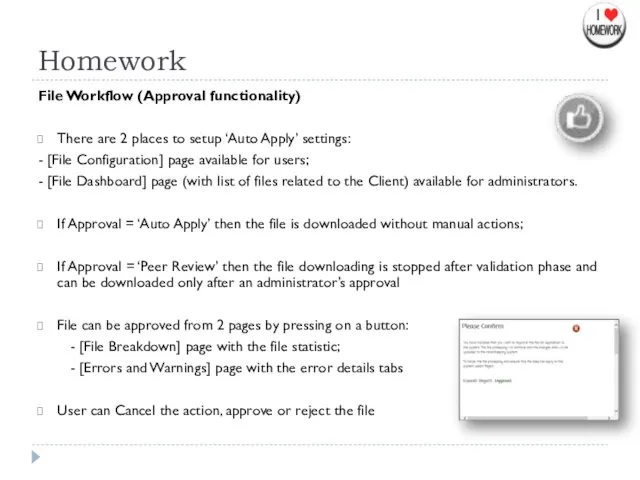 File Workflow (Approval functionality)
File Workflow (Approval functionality) Установка связи компьютеров с периферийными устройствами, среда передачи данных
Установка связи компьютеров с периферийными устройствами, среда передачи данных Проектирование сети поставщика интернет-услуг
Проектирование сети поставщика интернет-услуг ООО Айти-Услуги. Разработка программного обеспечения
ООО Айти-Услуги. Разработка программного обеспечения Дед Мороз. Рисуем в Paint
Дед Мороз. Рисуем в Paint Проблема развития виртуального предпринимательства в РФ
Проблема развития виртуального предпринимательства в РФ Игромания. Компьютерная зависимость
Игромания. Компьютерная зависимость Создание структурированного документа. Ур. 22
Создание структурированного документа. Ур. 22 Презентация на тему Геоинформационные системы в Интернете (ГИС)
Презентация на тему Геоинформационные системы в Интернете (ГИС)  Топология локальных сетей
Топология локальных сетей Транспортная задача как частный случай задач линейного программирования
Транспортная задача как частный случай задач линейного программирования 7-1-6
7-1-6 Введение в объектноориентированное программирование. Параметризованные типы
Введение в объектноориентированное программирование. Параметризованные типы Работа с файлами, каталогами и стандартными программами
Работа с файлами, каталогами и стандартными программами Знакомство с графическим оператором DRAW. Информатика 5 класс
Знакомство с графическим оператором DRAW. Информатика 5 класс Решение задач с циклом
Решение задач с циклом Основы современных операционных систем. Лекция 13
Основы современных операционных систем. Лекция 13 4 Двоичное кодирование
4 Двоичное кодирование Портал персонифицированного дополнительного образования Кировской области. Как получить сертификат дополнительного образования
Портал персонифицированного дополнительного образования Кировской области. Как получить сертификат дополнительного образования Инструкция заполнения заявления для предоставления субсидий на оплату ЖКУ через ПГУ
Инструкция заполнения заявления для предоставления субсидий на оплату ЖКУ через ПГУ Моделирование первой сессии
Моделирование первой сессии Укрощение строптивых. Оптимизация и реструктура проекта для увеличения доступности CodeEvening
Укрощение строптивых. Оптимизация и реструктура проекта для увеличения доступности CodeEvening Media – средства массовой информации
Media – средства массовой информации Русские термины
Русские термины Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств