Трудоёмкость алгоритмов

ФПМИ БГУ
Алгоритм
это конечная последовательность чётко определенных, реализуемых компьютером инструкций, предназначенная для решения определенного класса задач.
Переход от одного состояния к другому не обязательно детерминирован; некоторые алгоритмы рандомизированы.
Начиная с начального состояния и начального ввода (возможно, пустого), инструкции описывают вычисление, которое при выполнении проходит через конечное число чётко опредёленных последовательных состояний, в конечном итоге производя вывод и завершаясь в конечном состоянии.

Определение
Трудоёмкость алгоритма – это функция T(l), которая оценивает сверху время, требуемое для решения задачи.
Возникают вопросы:
С какими алгоритмами мы работаем, ведут ли они себя одинаково на одних и тех же входных данных при разных запусках алгоритма?
Как подсчитать время работы алгоритма? Какие входные данные надо учитывать?
Что такое размерность задачи l и как её подсчитать?
ФПМИ БГУ
Аргументом функции T является размерность задачи l.

В рамках нашей дисциплины мы будем работать с детерминированными алгоритмами.
Детерминированный алгоритм
Для одних и тех же входных данных все запуски алгоритма одинаковы по поведению.
Рандомизированный алгоритм
Предполагает в своей работе некоторый случайный выбор и время работы рандомизированного алгоритма зависит от этого выбора.
ФПМИ БГУ

Как подсчитать время работы детерминированного алгоритма ?
Модель вычислительного устройства:
Равнодоступная адресная машина (англ. Random-Access Machine - RAM).
На чём считать?
РАМ - универсальная математическая модель вычислений, которая является хорошим приближением к классу обычных вычислительных машин.

Равнодоступная адресная машина представляет собой вычислительную машину с одним сумматором, в котором команды программы не могут изменять сами себя.
РАМ состоит из входной ленты, с которой она может считывать данные в соответствии с их упорядоченностью, выходной ленты, на которую она может записывать (в первую свободную клетку), и памяти, которая состоит из последовательности регистров (ячейка с номером 0 – сумматор).
Программа - это последовательность команд (команды занумерованы числами 1,2, ….).
Есть счетчик команд – целое число.
Сама программа не записывается в память.
Команды процессора выполняются последовательно, одновременно выполняемые команды отсутствуют (однопроцессорная машина).

Элементарный шаг вычисления:
Если в качестве модели вычислений взять неветвящуюся программу и предположить, что алгоритм – это последовательность арифметических операций и все арифметические операции эквивалентны, т.е. затрачивают на свое выполнение одну единицу времени (равномерный весовой критерий), то время работы алгоритма – число операций алгоритма.
ФПМИ БГУ
Что считать?
В некоторых задачах (например, сортировка) удобно в качестве основной меры сложности брать число выполняемых команд разветвления.

ФПМИ БГУ
На практике ….
Программы, написанные на языках высокого уровня, нужно переводить в машинный код. Это можно делать по-разному.
Реальному ЦП требуется разное количество времени для выполнения различных операций.
C++ уже на этапе компиляции переводит инструкции программы в хорошо оптимизированный машинный код.
Python выполняет преобразования в машинный код на этапе выполнения со значительными накладными расходами.
Например, время выполнения операций на процессоре Intel Core десятого поколения (Ice Lake):​
add, sub, and, or, xor, shl, shr…: 1 такт
mul, imul: 3–4 такта
div, idiv (32-битный делитель): 12 тактов
div, idiv (64-битный делитель): 15 тактов
Подробнее о времени выполнения операций: https://www.agner.org/optimize/instruction_tables.pdf

На практике ….
Даже имея готовый ассемблерный код реализации алгоритма, не представляется возможным узнать, какое время потребуется для его выполнения. Для этого необходимо было бы учесть, в частности,
Кеширование данных. Процессоры имеют многоуровневую систему кешей (L1, L2, L3), постоянно сохраняющую те или иные ячейки для более быстрого доступа. В зависимости от того, закешировал ли процессор нужную ячейку, время доступа к данным может отличаться в десятки раз.
Out-of-order execution. Процессор способен выполнять несколько не зависящих друг от друга команд одновременно (например, последовательные mov eax, ecx и add edx, 5). Процессор просматривает программу на сотни инструкций вперёд, выискивая те, что может выполнить без очереди.
Branch prediction и Speculative execution. Большое препятствие для выполнения инструкций наперёд — ветвления (в частности, if'ы). Процессор не может заранее знать, в какую ветвь алгоритма ему придётся войти, и какой код ему нужно выполнять наперёд. Branch prediction модули следят за ходом выполнения программы и пытаются предсказать направления ветвлений (угадывают в >90% случаев). Штраф за ошибочное предсказание — потеря времени из-за избавления от десятков заранее подготовленных результатов операций и начала вычислений заново.
Подробнее: https://www.agner.org/optimize/microarchitecture.pdf
Информация подготовлена студентом ФПМИ
Владиславом Дмитриевичем Кощенко, 2022 год

ФПМИ БГУ
Если вы пишете на C ++ и решаете типичную алгоритмическую задачу, то можете предположить, что за 1 секунду вы сможете выполнить ~ 108 абстрактных операций.
Если вы делаете много делений, если вы обращаетесь к большому количеству памяти в случайном порядке, то вы сможете сделать гораздо меньше, ~ 107.
Если операции простые, а обращения к памяти локальные или последовательные, то вы сможете выполнить ~ 109 операций.
Грубо говоря ….

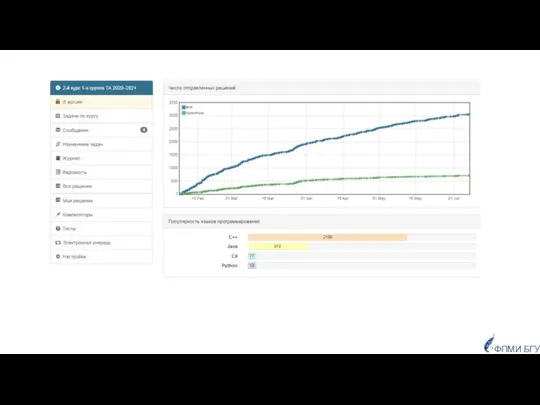
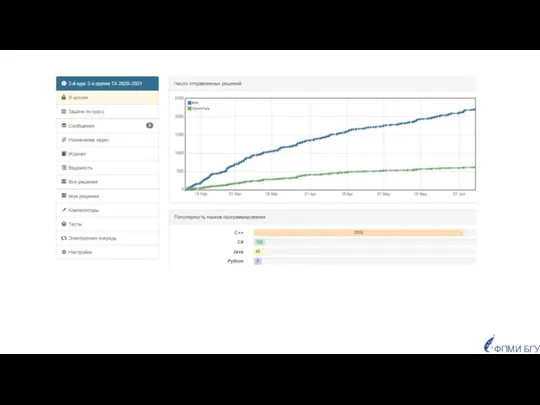
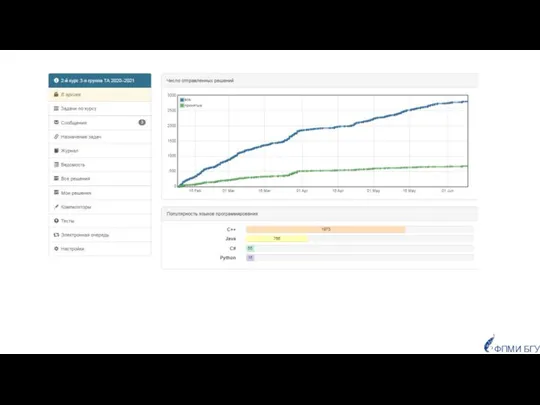
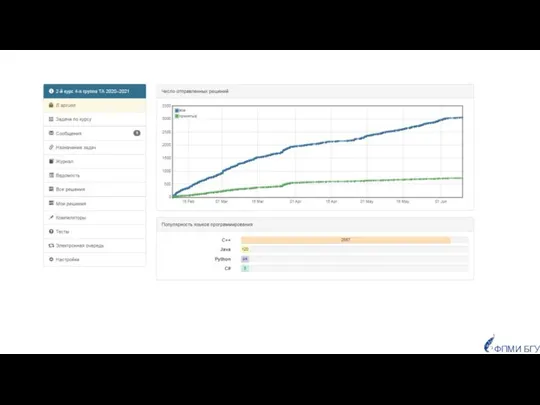
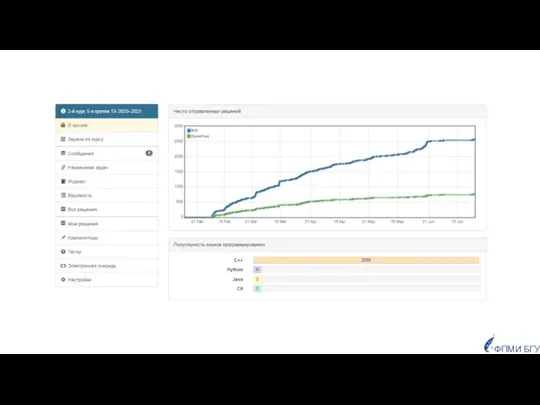
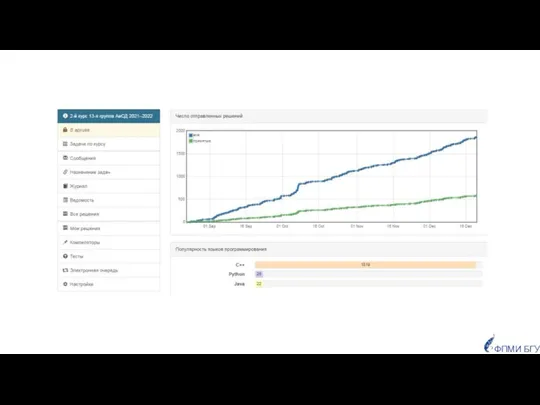
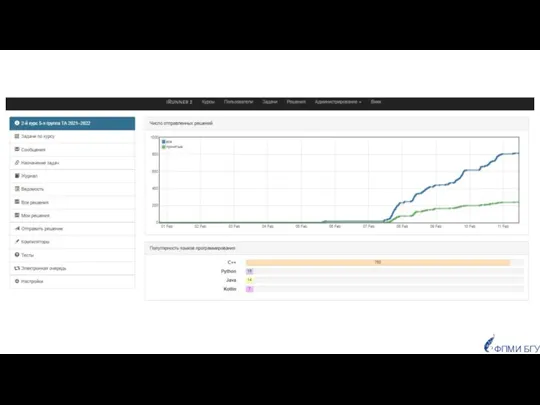
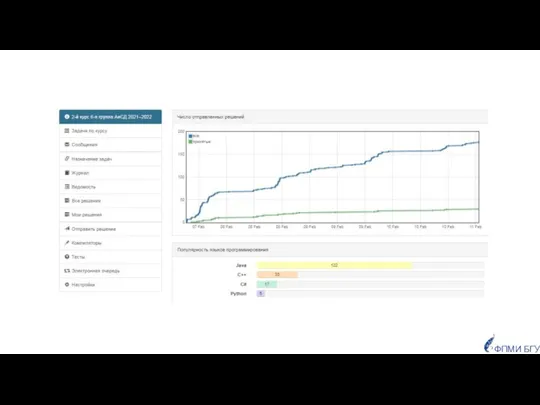
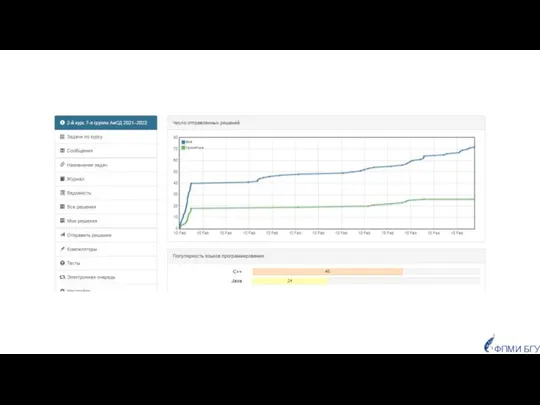
ФПМИ БГУ
Популярность языков программирования
у студентов

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ
2022 год

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

Для оценки времени работы детерминированного алгоритма в худшем случае будем искать такой набор входных данных, на котором алгоритм работает дольше всего.
Пример 1.
Последовательный поиск элемента x в произвольном массиве из n элементов.
Пример 2.
Сортировка массива из n элементов «пузырьком» (если на некоторой итерации нет ни одного обмена, то завершаем алгоритм).
ФПМИ БГУ
При этом нас будет интересовать порядок роста полученной функции, так как важна скорость роста функции при возрастании объема входных данных, т.е. оставляем только ту часть функции, которая с ростом аргумента к бесконечности, растёт быстрее всего.

Среднее время работы детерминированного алгоритма
по всем возможным наборам входных данных
Все входные данные разбиваем на группы так, чтобы время работы алгоритма для всех данных из одной группы было одним и тем же. Предположим, что у нас m групп.
Пусть pi – вероятность, с которой данные попадают в группу i.
Пусть ti –время работы алгоритма для данных из группы i.
Сведения из теории вероятности
Если у нас m групп и входные данные могут оказаться с равной вероятностью в любой из них, то
В этом случае среднее время работы алгоритма по всем возможным наборам входных данных:
ФПМИ БГУ

Пример.
Задан массив из n уникальных элементов и некоторое число x.
Необходимо определить есть ли число x в массиве.
Оценить среднее время работы алгоритма последовательного поиска по всем возможным наборам входных данных.
1-я группа: искомый элемент x стоит на 1-й позиции
2-я группа: искомый элемент x стоит на 2-й позиции
3-я группа: искомый элемент x стоит на 3-й позиции
n-я группа: искомый элемент x стоит на n-й позиции
…
(n+1)-я группа: искомого элемента x нет
…
ФПМИ БГУ

А как же подсчитать время работы рандомизированного алгоритма в худшем случае?
данные 1
1-й запуск алгоритма
2-й запуск алгоритма
……
K1-й запуск алгоритма
. . .
ФПМИ БГУ
данные 2
1-й запуск алгоритма
2-й запуск алгоритма
……
k2 -й запуск алгоритма
данные 3
1-й запуск алгоритма
2-й запуск алгоритма
……
k3 -й запуск алгоритма
данные m
1-й запуск алгоритма
2-й запуск алгоритма
……
km-й запуск алгоритма
. . .

Функции можно сгруппировать по скорости роста в три основных класса (три асимптотики):
о большое от f от n
омега большое от f от n
тэтта большое от f от n
ФПМИ БГУ

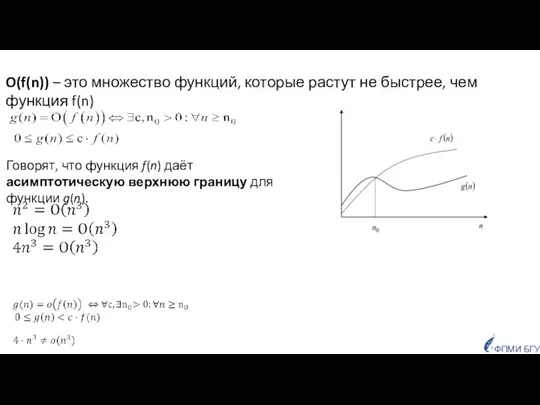
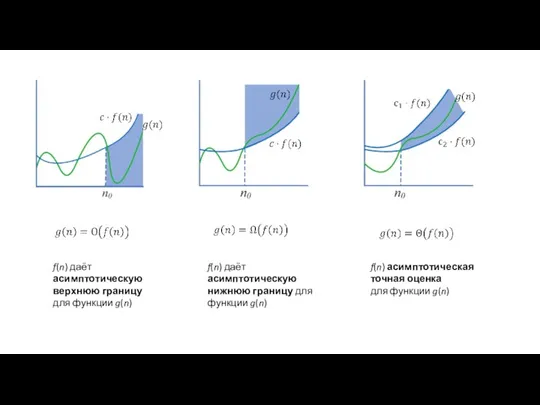
O(f(n)) – это множество функций, которые растут не быстрее, чем функция f(n)
Говорят, что функция f(n) даёт асимптотическую верхнюю границу для функции g(n).
ФПМИ БГУ

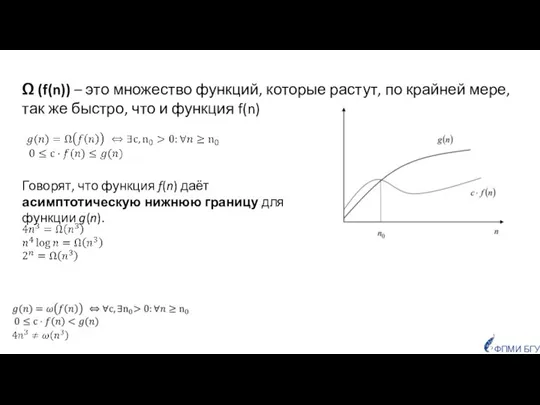
Ω (f(n)) – это множество функций, которые растут, по крайней мере, так же быстро, что и функция f(n)
Говорят, что функция f(n) даёт асимптотическую нижнюю границу для функции g(n).
ФПМИ БГУ

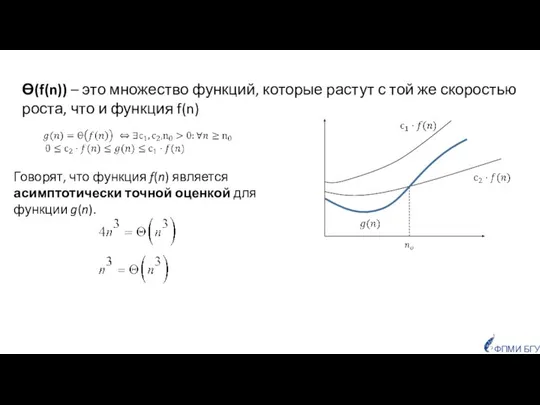
Ө(f(n)) – это множество функций, которые растут с той же скоростью роста, что и функция f(n)
Говорят, что функция f(n) является асимптотически точной оценкой для функции g(n).
ФПМИ БГУ

f(n) даёт асимптотическую верхнюю границу
для функции g(n)
f(n) даёт асимптотическую нижнюю границу для функции g(n)
f(n) асимптотическая точная оценка
для функции g(n)

ФПМИ БГУ
Скрытые под асимптотикой константы …
Доказательство
Константы можно выбрать и по-другому, однако важно не то, как их выбрать, а то, что такой выбор существует.

ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ

1. Время последовательного поиска элемента x в произвольном массиве из n элементов?
3. Время построения бинарного поискового дерева для последовательности из n чисел,
Дерево строится последовательным добавлением вновь поступающих элементов?
4. Время сортировки «пузырьком» последовательности из n элементов?
5. Время алгоритма определения числа x на простоту: делим x на все числа от 2 до ?
Оцените асимптотически
время работы в худшем случае
следующих алгоритмов
6. Время вычисления n!: последовательно перемножаем числа от 1 до n?
2. Время нахождения суммы всех элементов массива. В массиве n элементов.
ФПМИ БГУ

Трудоёмкость алгоритма –
это функция T(l), которая оценивает сверху время, требуемое для решения задачи.
Для того, чтобы найти трудоёмкость алгоритма, нужно время его работы
для его вычисления мы использовали равномерный весовой критерий, при котором каждая операция выполняется за 1 единицу времени и каждая ячейка занимает 1 единицу памяти
выразить через размерность задачи
логарифмический весовой критерий – объем памяти, необходимый для хранения числа, равен длине двоичного представления этого числа, а время выполнения команды пропорционально длине его операндов.
ФПМИ БГУ

ФПМИ БГУ

ФПМИ БГУ
Логарифмируем и, учитывая, что число бит является целым числом, получаем

ФПМИ БГУ
Логарифмируем и, учитывая, что число бит является целым числом, получаем

ФПМИ БГУ
Логарифмируем и, учитывая, что число бит является целым числом, получаем

ФПМИ БГУ

ФПМИ БГУ
Решение
Найдём множество возможных входных данных
где входным числом будем считать
Тогда

Решение
ФПМИ БГУ

Оценка трудоёмкости алгоритма
Сформулировали задачу и описали алгоритм её решения.
Вычислили время работы алгоритма (в худшем случае).
3) Вычислили размерность задачи (по входным данным задачи).
4) Выразили время работы алгоритма через размерность задачи и получили функцию T(l) - трудоёмкость алгоритма.
5) Теперь нужно сделать вывод о том, какой был разработан алгоритм: полиномиальный или экспоненциальный.
ФПМИ БГУ

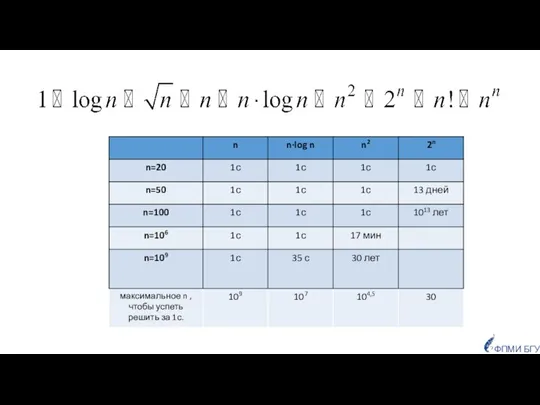
Сведения из математики
ФПМИ БГУ
Алгоритм называется полиномиальным, если его трудоемкость

Размерность задачи
Время работы алгоритма
Трудоёмкость
ФПМИ БГУ
Будем предполагать, что в результате суммирования не произойдёт переполнения.
Так как каждое число занимает C1 бит, то сложение двух чисел будет выполнено за время O(C1).
1-е число
2-е число
n-е число
…
биты

Сведения из математики
1) Экспоненциальная функция это функция:
2) Любая экспоненциальная функция возрастает быстрее полиномиальной функции.
ФПМИ БГУ
Алгоритм называется экспоненциальным, если его трудоемкость

ФПМИ БГУ
Размерность задачи
Время работы алгоритма
Трудоёмкость
биты

ФПМИ БГУ

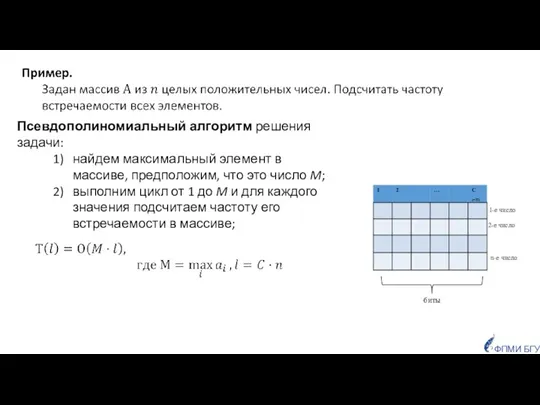
ФПМИ БГУ
1-е число
2-е число
n-е число
биты
Псевдополиномиальный алгоритм решения задачи:
найдем максимальный элемент в массиве, предположим, что это число M;
выполним цикл от 1 до M и для каждого значения подсчитаем частоту его встречаемости в массиве;

ФПМИ БГУ
Для задач, имеющих числовые параметры, псевдополиномиальные алгоритмы на практике ведут себя как экспоненциальные только при очень больших значениях числовых параметров индивидуальных задач.
Во всех случаях, кроме очень больших значений числового параметра (которые могут и не встречаться в реальных задачах), они работают, как полиномиальные.

ФПМИ БГУ

ФПМИ БГУ

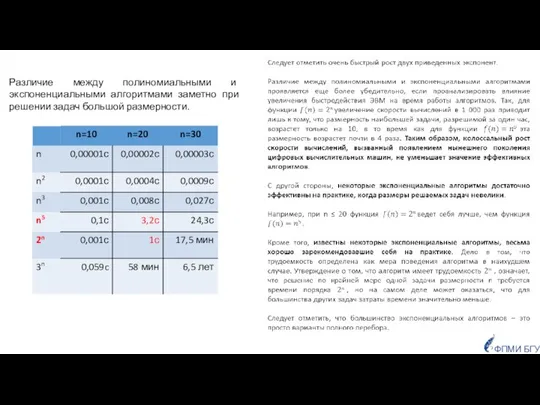
Различие между полиномиальными и экспоненциальными алгоритмами заметно при решении задач большой размерности.
ФПМИ БГУ

ФПМИ БГУ
Размерность задачи
биты
число n
полиномиальный или экспоненциальный?
полиномиальный или экспоненциальный?