Задачи математического программирования

1. Место математических моделей в теории управления

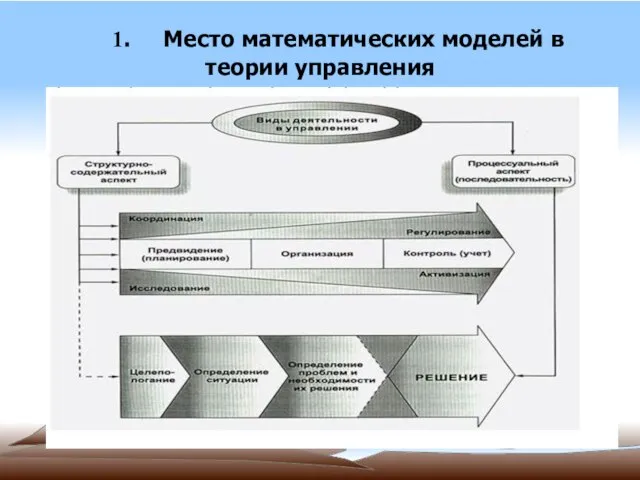
2. Классификация задач принятия решений
Основные классификационные признаки
1. Число целей операции, преследуемых одной оперирующей стороной
2. Наличие или отсутствие зависимости критерия оптимальности от времени
3. Наличие случайных и неопределенных факторов, влияющих на исход операции - «определенность - риск - неопределенность»

По первому классификационному признаку
ЗПР делятся на
- одноцелевые или однокритериальные (скалярные)
- многоцелевые или многокритериальные

По второму классификационному признаку
ЗПР делятся на
- статические
- динамические

По третьему классификационному признаку
ЗПР делятся на
- детерминированные — принятие решений при определенности
- стохастические — принятие решений в условиях риска
- принятие решений в условиях неопределенности

3. Классификация математических моделей
Математическая модель – это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему

Математическая модель принятия решения представляет собой формализацию схемы:
? : ? × ? → А,
где
? — множество допустимых альтернатив,
? — множество возможных состояний среды,
А — множество возможных исходов.
(?, ?), где ? ∈ ?, ? ∈ ? , соответствует определенный исход ? ∈ ?.

Основные этапы построения ММ:
1. Определение цели
2. Определение параметров модели
3. Формирование управляющих переменных
4. Определение области допустимых решений
5. Выявление неизвестных факторов
6. Выражение цели через управляющие переменные, параметры и неизвестные факторы, т.е. формирование целевой функции

Решить задачу — значит найти такое
? ∈ Х ,
чтобы при данных фиксированных параметрах
y ∈ Y,
значение ? ∈ ?. было оптимальным

Основные принципы построения ММ:
1. Необходимо согласовать точность и подробность модели
2. Математическая модель должна отражать существенные черты исследуемого явления и при этом не должна его сильно упрощать.
3. Математическая модель не может быть полностью адекватна реальному явлению, поэтому для его исследования лучше использовать несколько моделей, для построения которых применены разные математические методы.
4. Математическая модель должна быть устойчивой, т.е. сохранять свои свойства и структуру при этих воздействиях.