Слайд 2Законы алгебры логики
Рефлективности
a ∨ a = a; a & a = a
Коммутативности
a

∨ b = b ∨ a; a & b = b & a
Ассоциативности
(a & b) & c = a & (b & c)
(a ∨ b) ∨ c = a ∨ (b ∨ c)
Дистрибутивности
a & (b ∨ c) = a & b ∨ a & c
a ∨ b & c = (a ∨ b) & (a ∨ c)
Склеивания
x & y ∨ x & ¬ y = x; (x ∨ y) & ( x ∨ ¬ y) = x
Слайд 3Пример 1
Вычислить значение логической формулы:
¬X ∨ Y ∨ X ∨ Z
если логические

переменные имеют следующие значения: X = ложь, Y = истина, Z = истина
Слайд 5Составить таблицу истинности для выражения
Пример 3

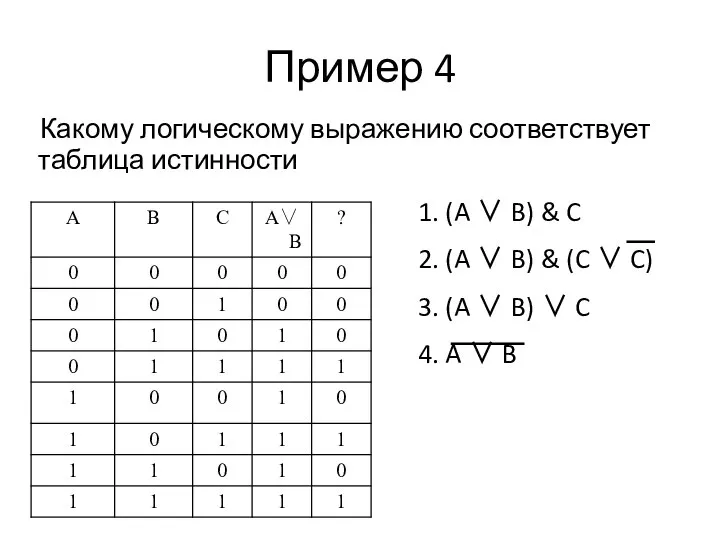
Слайд 6Пример 4
Какому логическому выражению соответствует таблица истинности





 Insignia. Идея
Insignia. Идея Основные устройства компьютера
Основные устройства компьютера Уровни тестирования (2)
Уровни тестирования (2) FreeJam icon. Иконки
FreeJam icon. Иконки Устранение цифрового неравенства в Матвеевском районе
Устранение цифрового неравенства в Матвеевском районе Магистерская программа Моделирование в биотехническом приборостроении
Магистерская программа Моделирование в биотехническом приборостроении Виртуальная экскурсия. Основные преимущества и недостатки
Виртуальная экскурсия. Основные преимущества и недостатки Как получить сертификат ПФДО
Как получить сертификат ПФДО Перспективы продвижения ореха грецкого в Центральном Черноземье
Перспективы продвижения ореха грецкого в Центральном Черноземье ПР кроссворд и тест
ПР кроссворд и тест Применение программы Tinkercad для проведения уроков Технология, в том числе при дистанционной работе
Применение программы Tinkercad для проведения уроков Технология, в том числе при дистанционной работе Презентация на тему Информационные процессы
Презентация на тему Информационные процессы  Доступ к системе создания сайтов
Доступ к системе создания сайтов Теги и атрибуты HTML
Теги и атрибуты HTML Клавиатура – средство общения человека с компьютером
Клавиатура – средство общения человека с компьютером Вычислительные приспособления и устройства
Вычислительные приспособления и устройства Мобильная безопасность
Мобильная безопасность GenPLAN
GenPLAN Lect_1_JS (1)
Lect_1_JS (1) SIM kartiniz. Sisteminizi temizlemeniz gerekiyor
SIM kartiniz. Sisteminizi temizlemeniz gerekiyor Industry (services): Chatbot for the fast events search within the city
Industry (services): Chatbot for the fast events search within the city АО ТомскНИПИнефть: Общая информация об институте
АО ТомскНИПИнефть: Общая информация об институте Обеспечение технологической устойчивости объектов ДЭЗ за счёт внедрения цифровизации и передовых технологий
Обеспечение технологической устойчивости объектов ДЭЗ за счёт внедрения цифровизации и передовых технологий Живая классика
Живая классика Кодирование текстовой и графической информации
Кодирование текстовой и графической информации Назначение и форматирование таблиц. 7 класс
Назначение и форматирование таблиц. 7 класс Операционные системы и базы данных
Операционные системы и базы данных Презентация на тему Представление об объектах окружающего мира
Презентация на тему Представление об объектах окружающего мира