Содержание
- 2. Цели и задачи урока: Повторение понятия прямоугольника, опираясь на полученные знания в курсе математики 1-6 классов
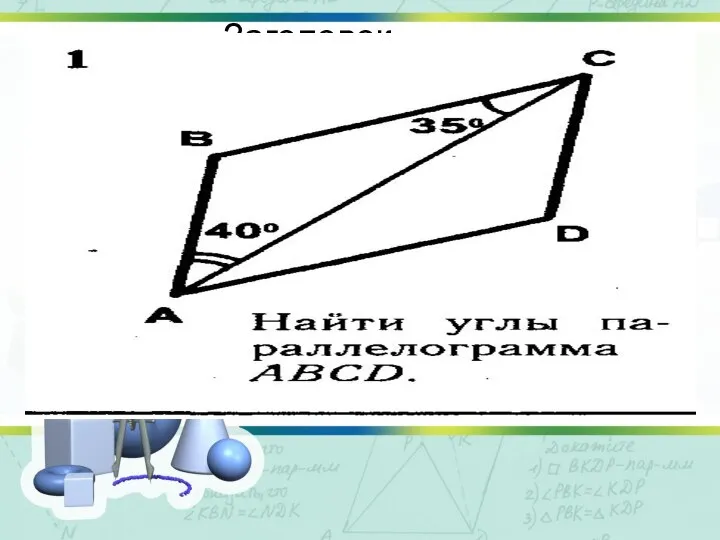
- 3. Устно решить задачи 1) Найти углы выпуклого четырехугольника, если их углы пропорциональны числам 1:2:3:4. 2).Найти углы
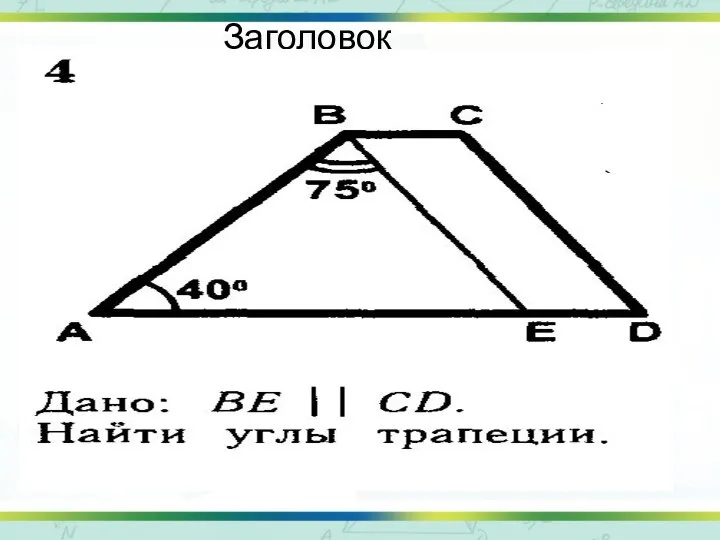
- 4. Заголовок слайда
- 5. Заголовок слайда
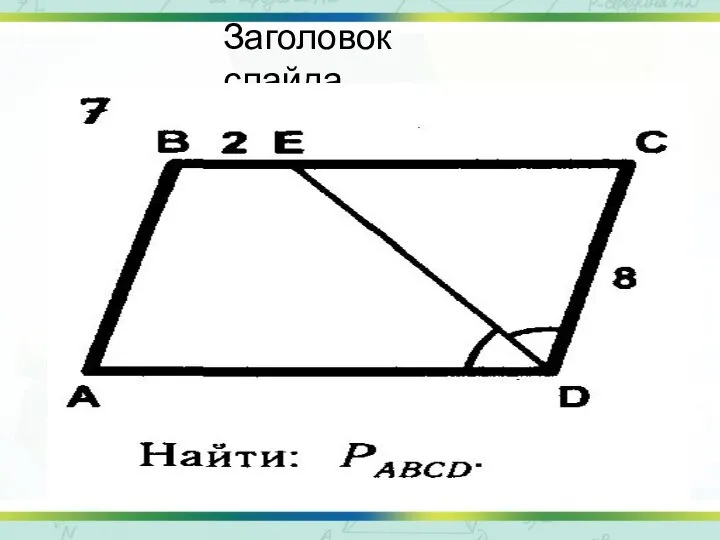
- 6. Заголовок слайда
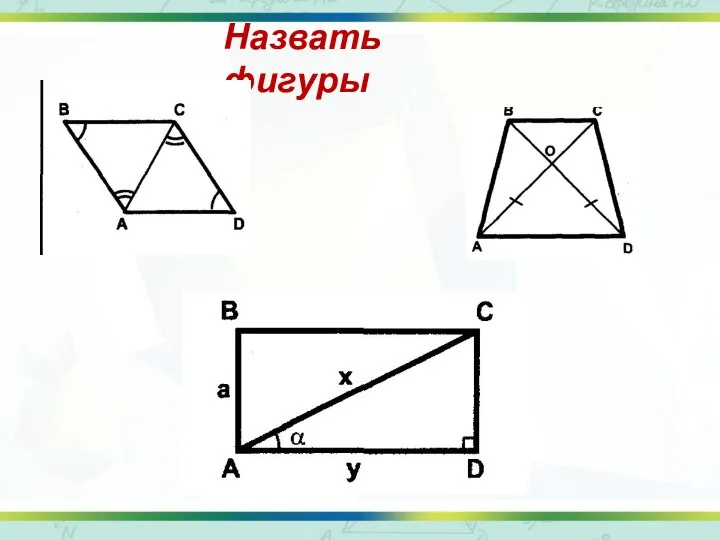
- 7. Назвать фигуры
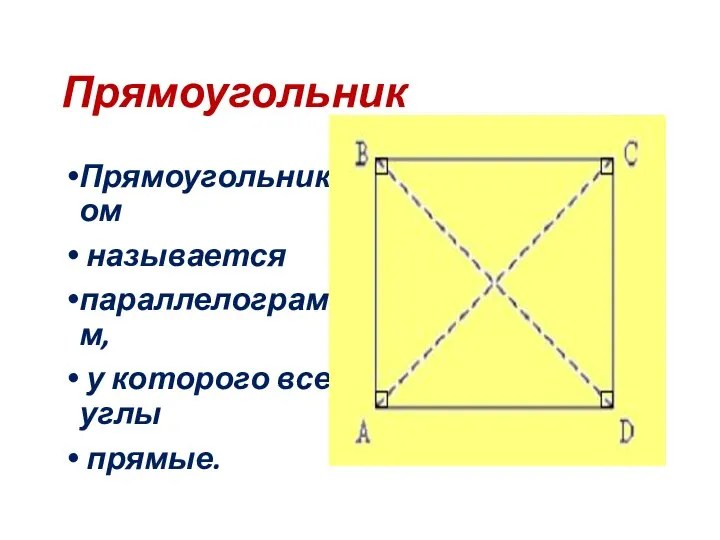
- 8. Прямоугольник Прямоугольником называется параллелограмм, у которого все углы прямые.
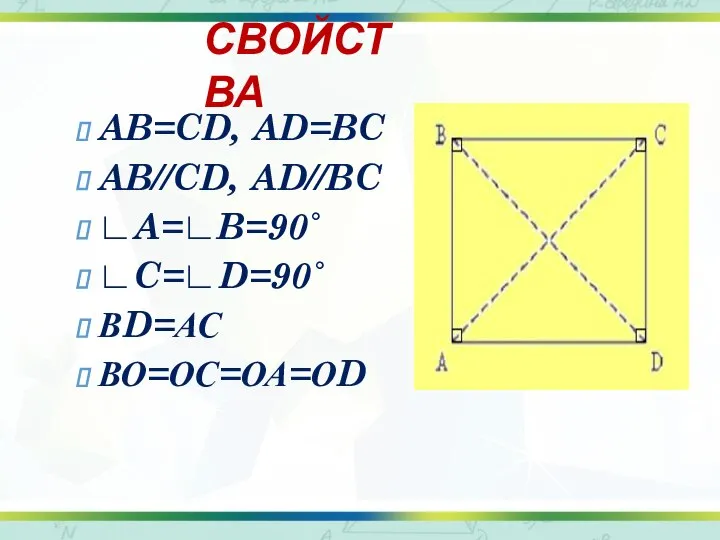
- 9. СВОЙСТВА AB=CD, AD=BC AB//CD, AD//BC ∟A=∟B=90˚ ∟C=∟D=90˚ ВD=АС ВО=ОС=ОА=ОD
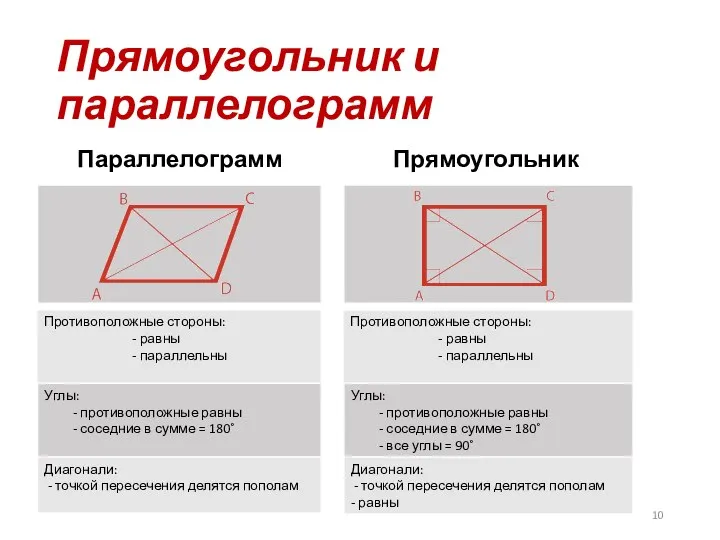
- 10. Прямоугольник и параллелограмм Параллелограмм Прямоугольник
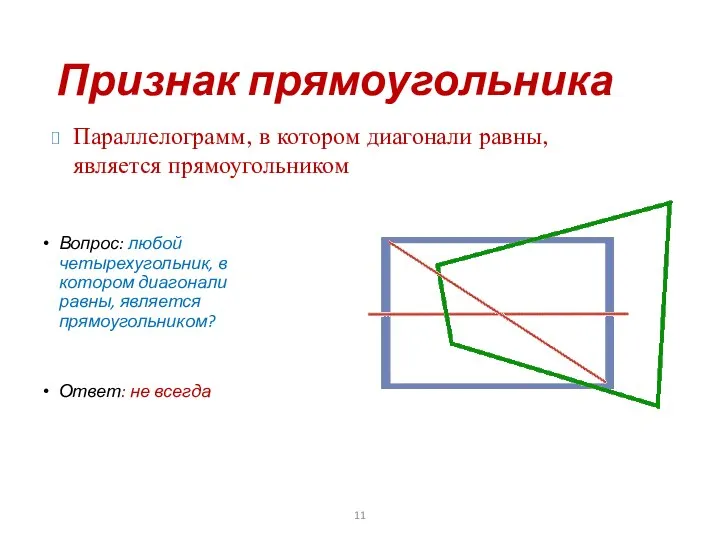
- 11. Признак прямоугольника Вопрос: любой четырехугольник, в котором диагонали равны, является прямоугольником? Ответ: не всегда Параллелограмм, в
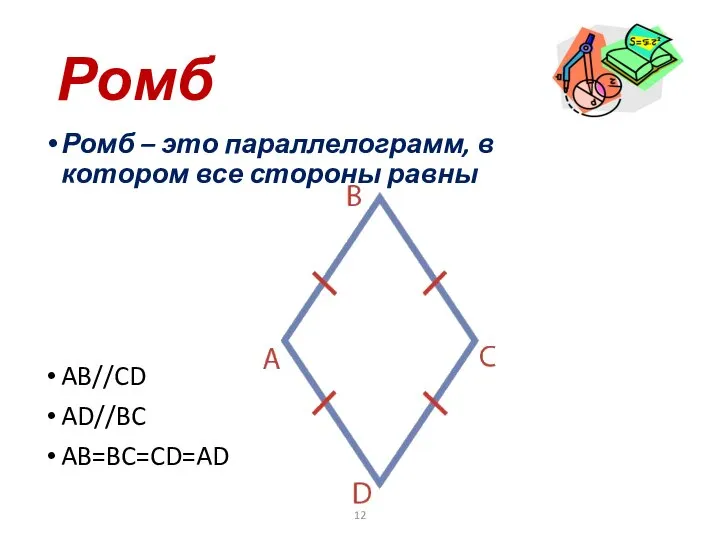
- 12. Ромб Ромб – это параллелограмм, в котором все стороны равны AB//CD AD//BC AB=BC=CD=AD
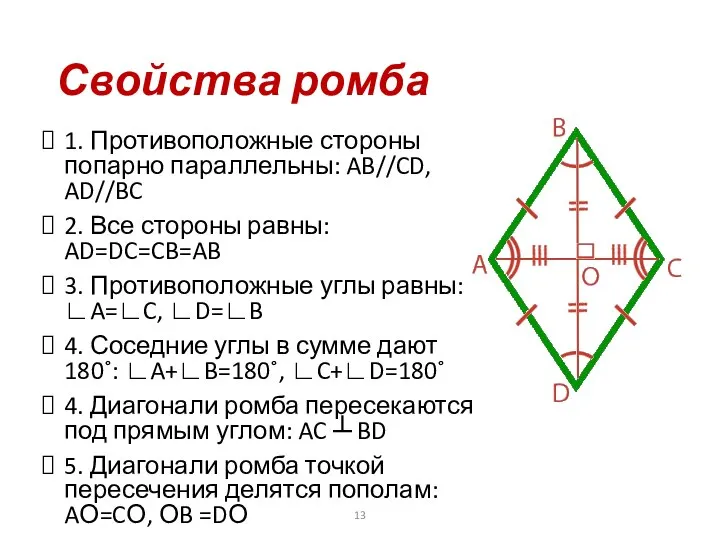
- 13. Свойства ромба 1. Противоположные стороны попарно параллельны: AB//CD, AD//BC 2. Все стороны равны: AD=DC=CB=AB 3. Противоположные
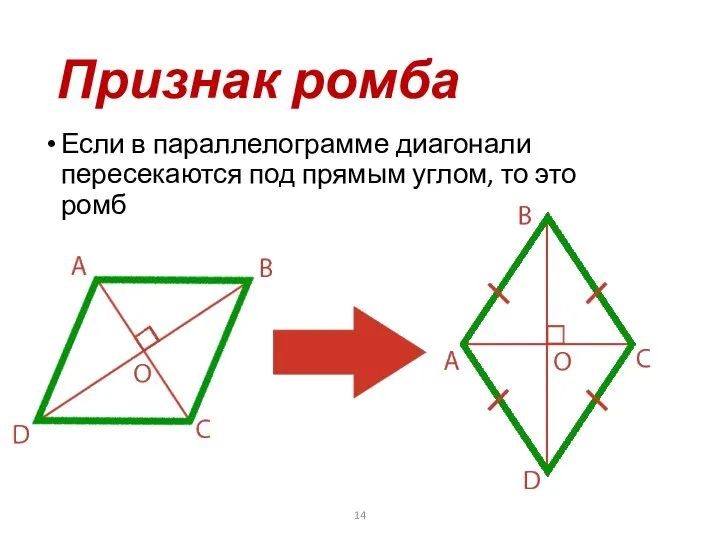
- 14. Признак ромба Если в параллелограмме диагонали пересекаются под прямым углом, то это ромб
- 15. Квадрат Если соединить в одной фигуре свойства прямоугольника и ромба, то мы получим КВАДРАТ
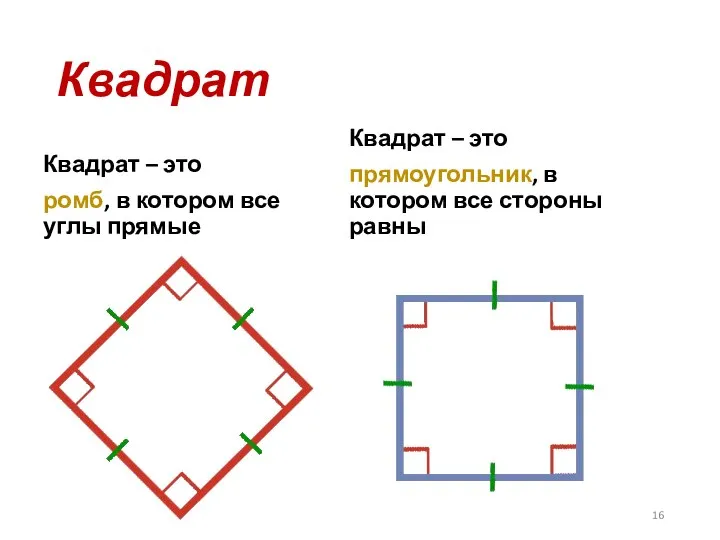
- 16. Квадрат Квадрат – это ромб, в котором все углы прямые Квадрат – это прямоугольник, в котором
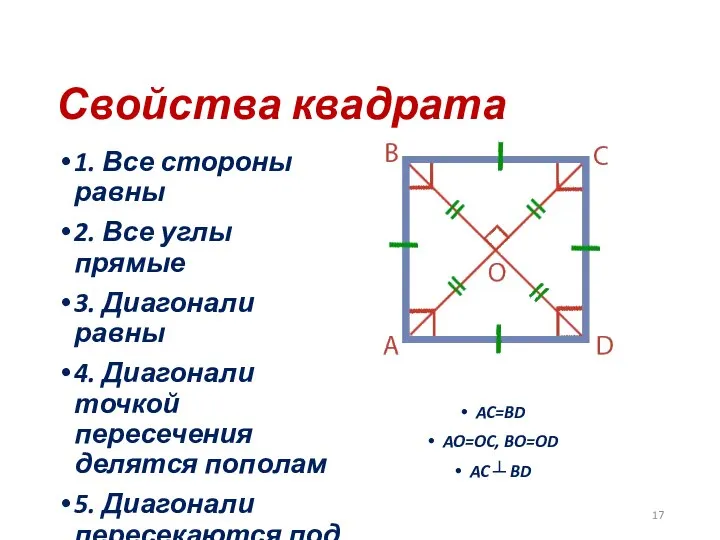
- 17. Свойства квадрата 1. Все стороны равны 2. Все углы прямые 3. Диагонали равны 4. Диагонали точкой
- 18. Признаки квадрата Если в прямоугольнике диагонали перпендикулярны – это квадрат Если в ромбе диагонали равны –
- 20. Скачать презентацию




 Төзек күпкырлыклар
Төзек күпкырлыклар Функция. Свойства функции
Функция. Свойства функции Презентация на тему Решение показательных уравнений 11 класс
Презентация на тему Решение показательных уравнений 11 класс  Презентация на тему Великие русские математики
Презентация на тему Великие русские математики  Свойства равнобедренного треугольника
Свойства равнобедренного треугольника Окружность, круг, их элементы и части. Центральный угол. 7 класс
Окружность, круг, их элементы и части. Центральный угол. 7 класс Презентация на тему Логарифмическая линия в ЕГЭ - 2011
Презентация на тему Логарифмическая линия в ЕГЭ - 2011  Древние и новые счеты. Делала Алина Семенова 5 г класс учительВера Николаевна Афанасьева Моу Сош № 59
Древние и новые счеты. Делала Алина Семенова 5 г класс учительВера Николаевна Афанасьева Моу Сош № 59 Умножение обыкновенных дробей
Умножение обыкновенных дробей Перенос запятой на один знак
Перенос запятой на один знак Правильные многогранники. Формула Эйлера. Правильные многогранники в философской картине мира Платона. Кубок Кеплера
Правильные многогранники. Формула Эйлера. Правильные многогранники в философской картине мира Платона. Кубок Кеплера Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)
Презентация на тему Умножение и деление чисел на 2 и на 3 (2 класс)  Пересечение поверхностей. Лекция 8
Пересечение поверхностей. Лекция 8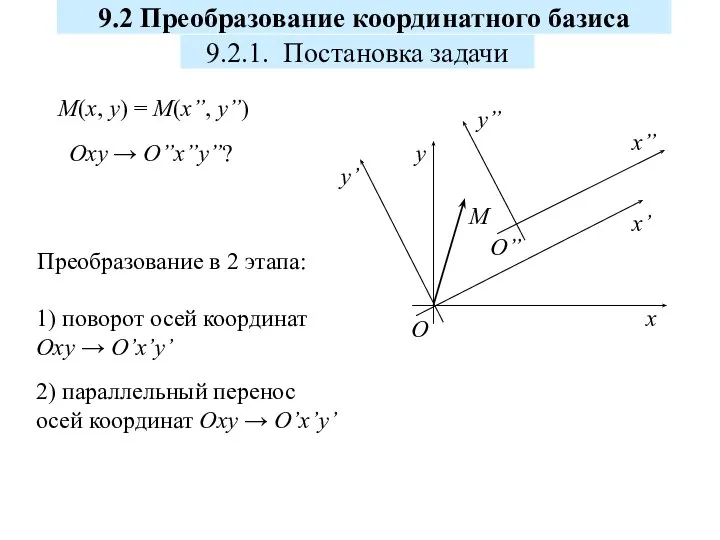 Преобразование координатного базиса
Преобразование координатного базиса Презентация по математике "Логарифмическая функция. Преобразования графиков." -
Презентация по математике "Логарифмическая функция. Преобразования графиков." -  Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной
Нахождение наибольшего и наименьшего значений функции на отрезке с помощью производной Контрольная работа № 7
Контрольная работа № 7 Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі
Функцияның нүктедегі шегі туралы ұғым және функцияның үзіліссіздігі Вписанные окружности (решение задач)
Вписанные окружности (решение задач) Графики тригонометрических функций. 10 класс
Графики тригонометрических функций. 10 класс Подготовка к ВПР
Подготовка к ВПР Презентация на тему Государственная политика противодействия наркотизму
Презентация на тему Государственная политика противодействия наркотизму  Таблица умножение на двух значное число
Таблица умножение на двух значное число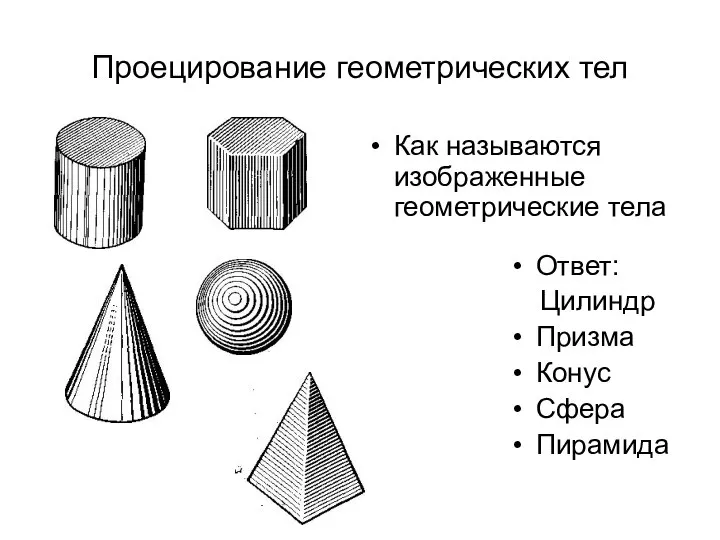 Построение геометрических тел
Построение геометрических тел Стереометрия. Аксиомы стереометрии
Стереометрия. Аксиомы стереометрии Таблица умножения и деления. Тренажёр на скорость
Таблица умножения и деления. Тренажёр на скорость Площадь прямоугольника
Площадь прямоугольника Простейшие тригонометрические уравнения
Простейшие тригонометрические уравнения