Содержание
- 2. Прямая и окружность Сколько общих точек могут иметь прямая и окружность? О
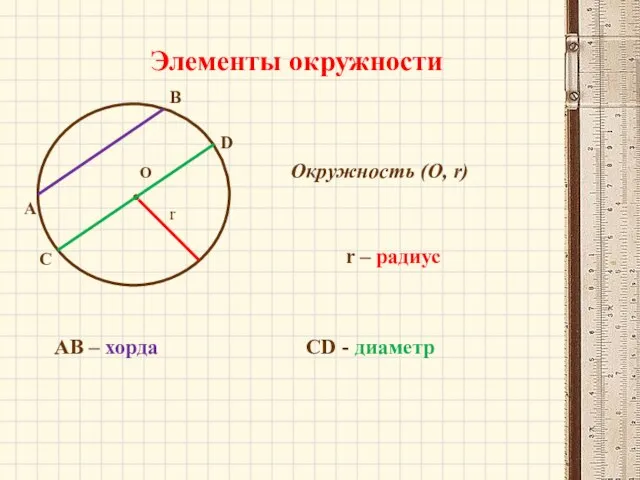
- 3. О Элементы окружности Окружность (О, r) r – радиус r A B АВ – хорда С
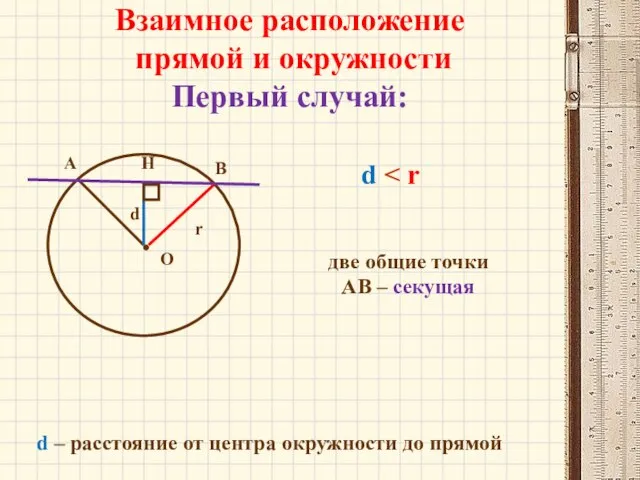
- 4. Взаимное расположение прямой и окружности Первый случай: d – расстояние от центра окружности до прямой О
- 5. Взаимное расположение прямой и окружности Второй случай: О Н r одна общая точка d = r
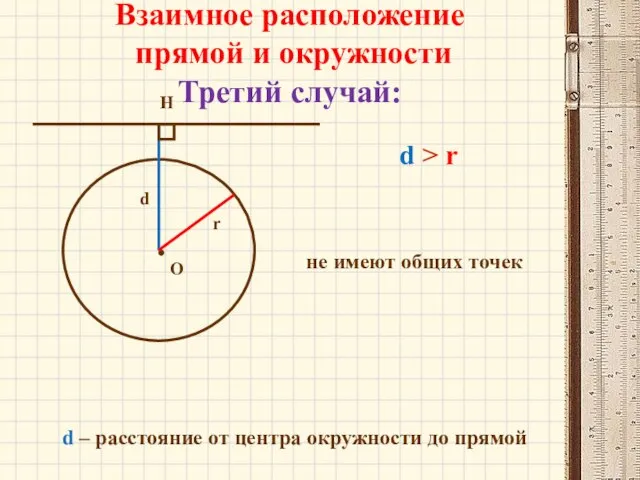
- 6. Взаимное расположение прямой и окружности Третий случай: О H d r d > r d –
- 7. Взаимное расположение прямой и окружности d d = r d > r две общие точки одна
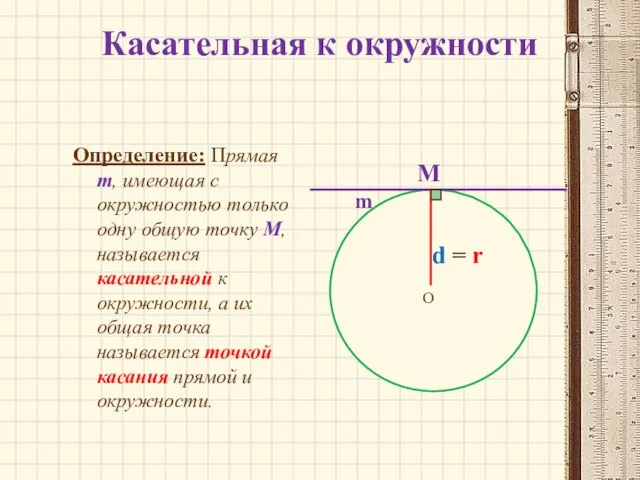
- 8. Касательная к окружности Определение: Прямая m, имеющая с окружностью только одну общую точку M, называется касательной
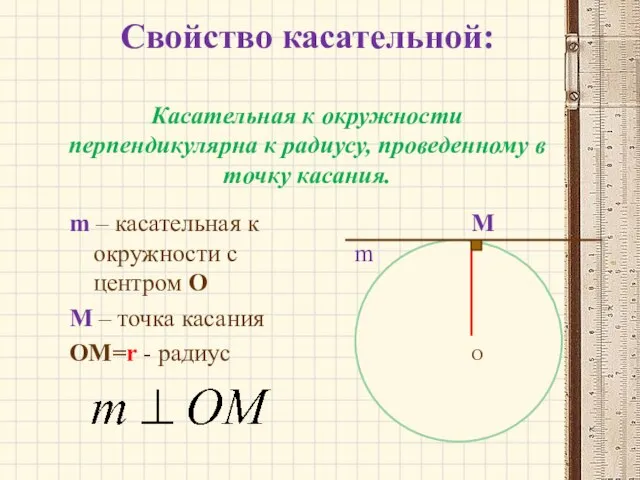
- 9. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. m – касательная к
- 11. Скачать презентацию



 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Презентация на тему Готфрид Вильгельм Лейбниц
Презентация на тему Готфрид Вильгельм Лейбниц  Консультація до іспиту ТМДМ
Консультація до іспиту ТМДМ Презентация на тему Геометрические тела. Многогранники
Презентация на тему Геометрические тела. Многогранники  Признаки равенства треугольников
Признаки равенства треугольников Математический марафон
Математический марафон Функция. График функции
Функция. График функции Задачи на разрезание
Задачи на разрезание Иррациональные неравенства
Иррациональные неравенства Четырёхугольники. Задачи на готовых чертежах
Четырёхугольники. Задачи на готовых чертежах Решение систем уравнений способом подстановки
Решение систем уравнений способом подстановки ГИА - 2016. Задачи №9,10,11,12
ГИА - 2016. Задачи №9,10,11,12 Параллелограмм
Параллелограмм Уравнение плоскости
Уравнение плоскости Решение тригонометрических уравнений sin а
Решение тригонометрических уравнений sin а Имитационное моделирование
Имитационное моделирование Вычитание смешанных чисел. 5 класс
Вычитание смешанных чисел. 5 класс Метод рекуррентных соотношений
Метод рекуррентных соотношений Задача по математике (1 класс, задание 15)
Задача по математике (1 класс, задание 15) ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Свойства корня степени n
Свойства корня степени n Владимир Модестович Брадис и его замечательные таблицы
Владимир Модестович Брадис и его замечательные таблицы Арксинус. Решение уравнения Sin t = a
Арксинус. Решение уравнения Sin t = a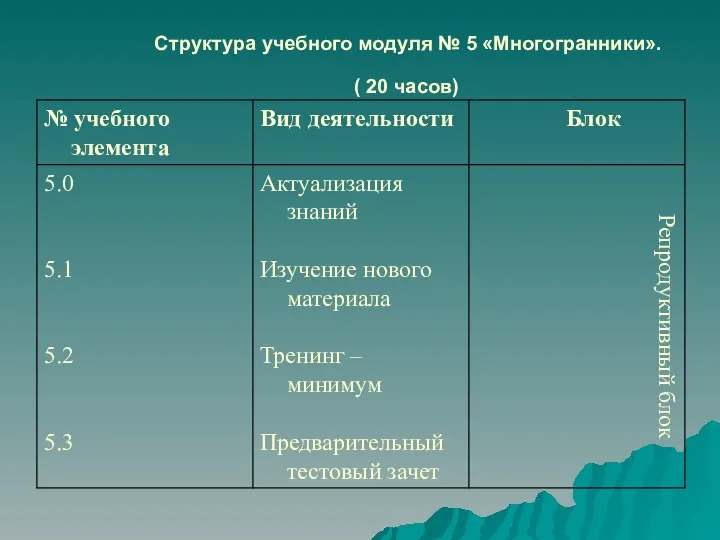 Структура учебного модуля № 5 Многогранники. ( 20 часов)
Структура учебного модуля № 5 Многогранники. ( 20 часов) Презентация на тему Звездчатые многогранники
Презентация на тему Звездчатые многогранники  Функции у=|x| и ей график
Функции у=|x| и ей график Стационарный режим теплообмена с фазовым переходом
Стационарный режим теплообмена с фазовым переходом Прямоугольник
Прямоугольник