Содержание
- 2. СОДЕРЖАНИЕ 1. Введение 2. Повторение Простейшие тригонометрические уравнения Частные случаи Задания для на повторение 4. Уравнения,
- 3. Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон
- 4. ТРИГОНОМЕТРИЯ - математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, с помощью которых
- 5. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Если уравнение не имеет решения. Если Если уравнение не имеет решения. Если
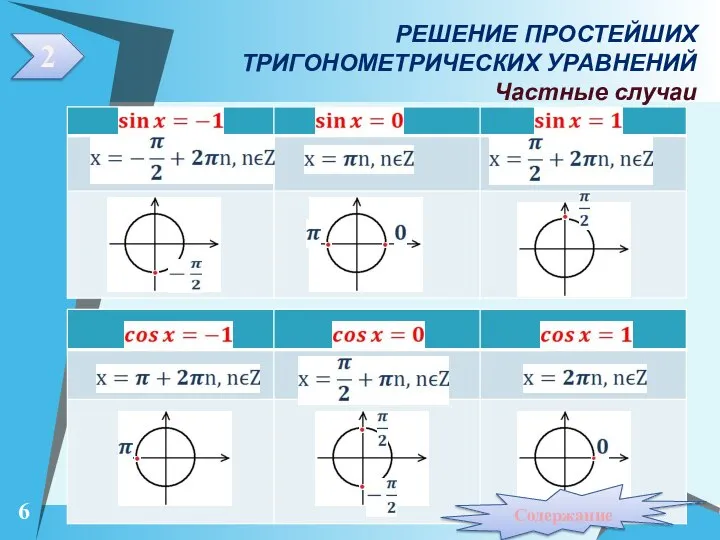
- 6. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Частные случаи 2 Содержание 6
- 7. 1. Решите уравнение: 1) 2) 3) 4) 2. Решите уравнение: 1) 2) 3) 4) 3. Укажите
- 8. УРАВНЕНИЯ, ПРИВОДИМЫЕ К АЛГЕБРАИЧЕСКИМ С помощью замены переменной можно привести тригонометрическое уравнение к алгебраическому. Рассмотрим несколько
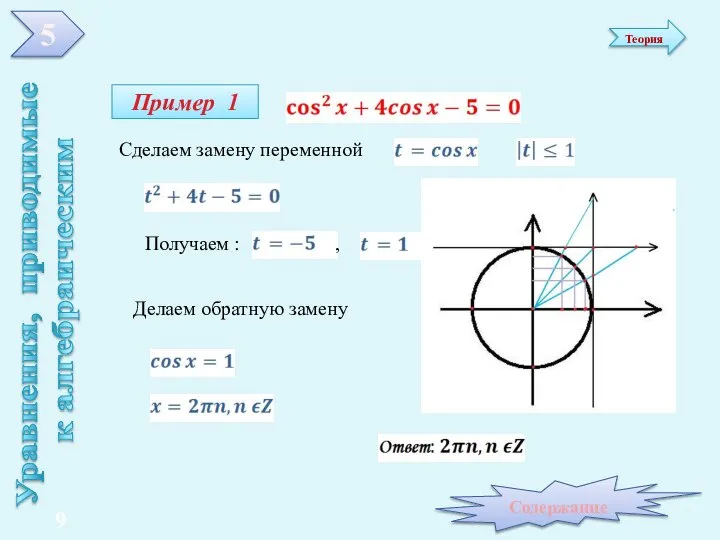
- 9. Делаем обратную замену , Пример 1 Уравнения, приводимые к алгебраическим Сделаем замену переменной Получаем : ,
- 10. Получаем : , Уравнения, приводимые к алгебраическим Сделаем замену переменной Применим основное тригонометрическое тождество 5 Пример
- 11. Пример 3 Уравнения, приводимые к алгебраическим Сделаем замену переменной Получаем : , 5 Содержание 11 Теория
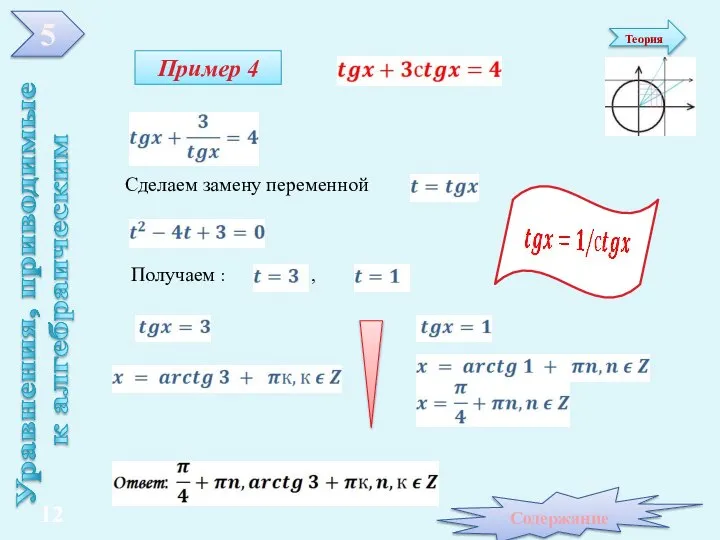
- 12. Получаем : , Пример 4 Уравнения, приводимые к алгебраическим Сделаем замену переменной 5 Содержание 12 Теория
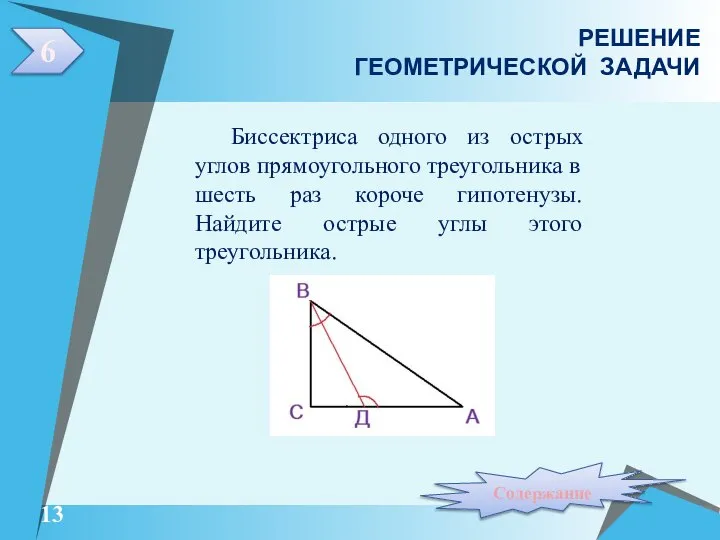
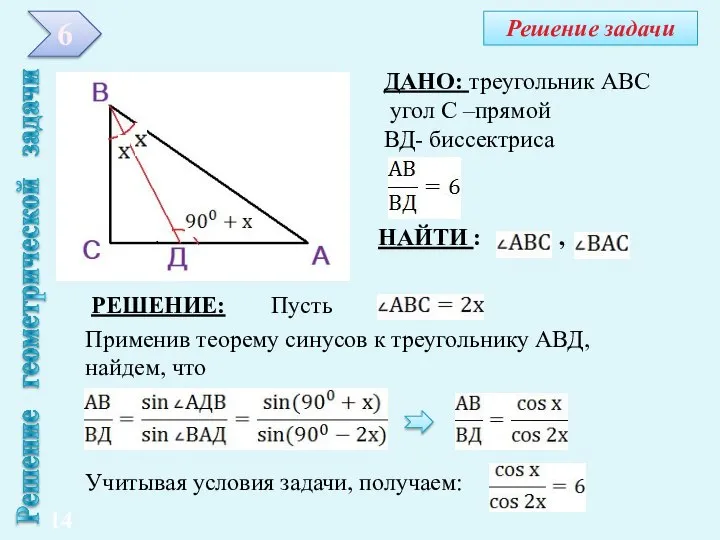
- 13. 6 РЕШЕНИЕ ГЕОМЕТРИЧЕСКОЙ ЗАДАЧИ Биссектриса одного из острых углов прямоугольного треугольника в шесть раз короче гипотенузы.
- 14. ДАНО: треугольник АВС угол С –прямой ВД- биссектриса НАЙТИ : , РЕШЕНИЕ: Пусть Применив теорему синусов
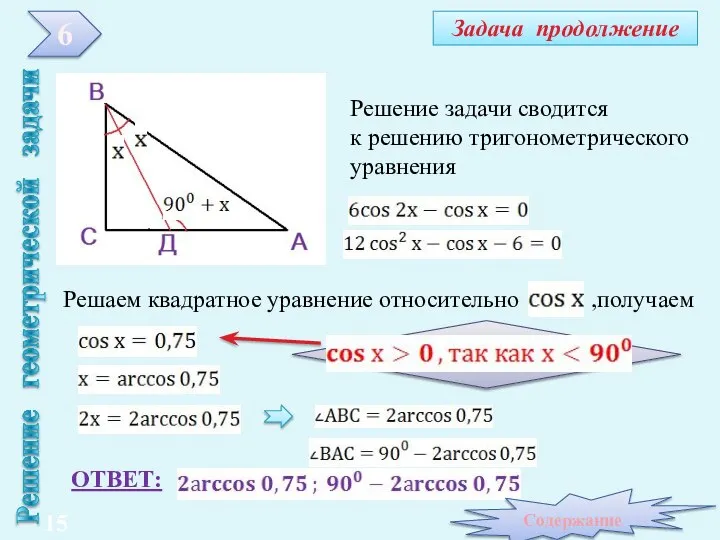
- 15. Задача продолжение Решение геометрической задачи ОТВЕТ: 6 Решение задачи сводится к решению тригонометрического уравнения Решаем квадратное
- 16. КРАТКИЙ СПРАВОЧНИК ФОРМУЛ 8 Нахождение тригонометрических функций по единичной окружности Основные тригонометрические тождества Формулы двойного аргумента
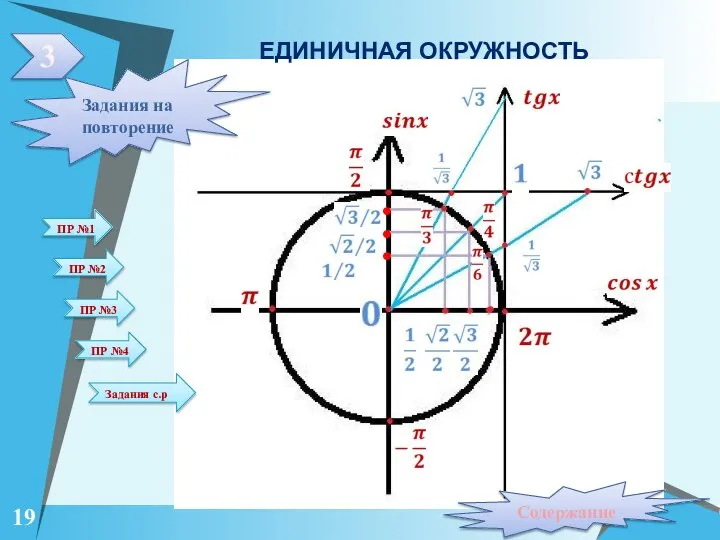
- 17. ЕДИНИЧНАЯ ОКРУЖНОСТЬ . . . 3 Содержание Задания на повторение 19 ПР №1 ПР №2 ПР
- 18. Краткий справочник формул 8 20
- 19. Краткий справочник формул 8 55 19
- 21. Скачать презентацию











 Моделирование информационных систем
Моделирование информационных систем Чертёж призмы
Чертёж призмы Аналитическая геометрия. Прямая на плоскости
Аналитическая геометрия. Прямая на плоскости Решение логарифмических уравнений
Решение логарифмических уравнений Осевая и центральная симметрии
Осевая и центральная симметрии калькуятор
калькуятор Решение систем неравенств. 8 класс
Решение систем неравенств. 8 класс Векторы. 9 класс
Векторы. 9 класс Теория фракталов
Теория фракталов Тригонометрические тождества
Тригонометрические тождества Вероятность равновозможных событий
Вероятность равновозможных событий Презентация на тему Сложение с переходом через десяток
Презентация на тему Сложение с переходом через десяток  Справочный материал к практике 11 по дисциплине Математика для студентов направления подготовки
Справочный материал к практике 11 по дисциплине Математика для студентов направления подготовки Среднее арифметическое
Среднее арифметическое Решение примеров в пределах 10
Решение примеров в пределах 10 Домашнее задание. Примеры и уравнения
Домашнее задание. Примеры и уравнения Решение задач на проценты. 6 класс. Урок 1
Решение задач на проценты. 6 класс. Урок 1 Двугранный угол
Двугранный угол Кратное числа
Кратное числа Презентация на тему Математическая викторина
Презентация на тему Математическая викторина  Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел
Презентация на тему Обозначение натуральных чисел.Чтение и запись натуральных чисел  Векторы в пространстве
Векторы в пространстве Рівняння. Основні властивості рівняння
Рівняння. Основні властивості рівняння Теорема о прямой, перпендикулярной к плоскости
Теорема о прямой, перпендикулярной к плоскости Учимся решать комбинаторные задачи. 4 класс
Учимся решать комбинаторные задачи. 4 класс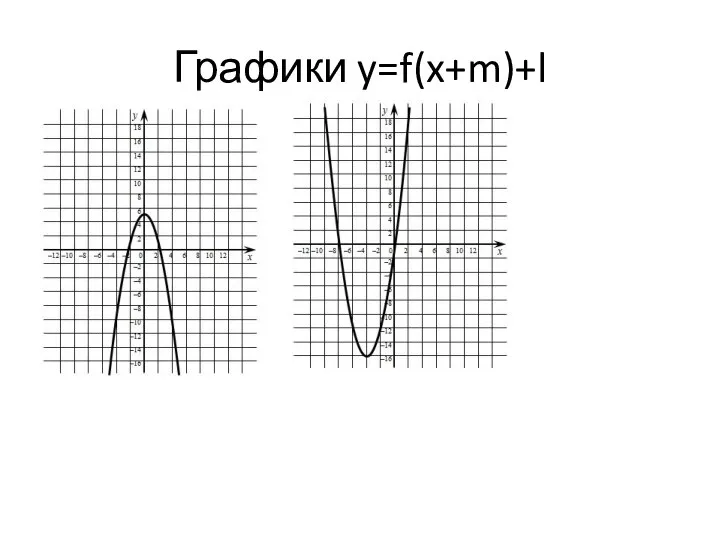 Графики y=f(x+m)+l
Графики y=f(x+m)+l Обыкновенные дроби (с использованием контрольно-измерительных материалов)
Обыкновенные дроби (с использованием контрольно-измерительных материалов) Разложение функций в степенные ряды
Разложение функций в степенные ряды