Слайд 2Содержание
Алфавит
Формулы
Аксиомы
Правило вывода
Правило подстановки
Теорема дедукции
Свойства исчисления высказываний

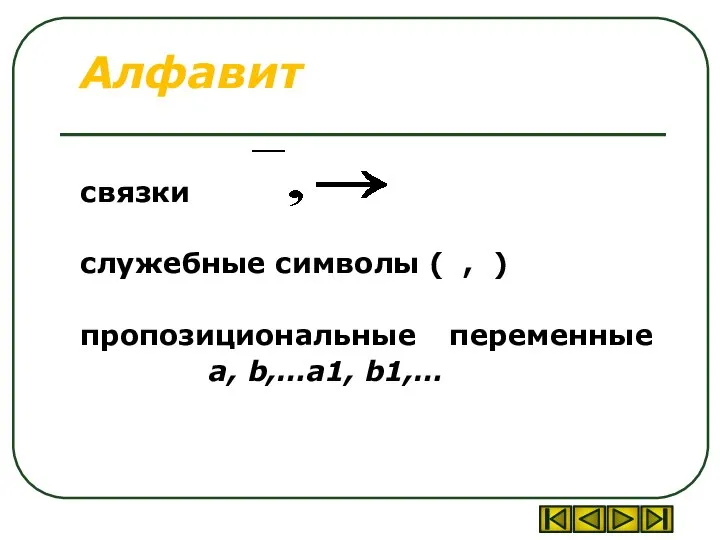
Слайд 3Алфавит
связки
служебные символы ( , )
пропозициональные переменные
a, b,…a1, b1,…
.
Слайд 4Формулы
1. Переменные суть формулы
2. Если А, В формулы, то
- тоже

формулы
Слайд 6Правило вывода
правило отделения или правило заключения (MP)

Слайд 7Интерпретация
Функция h называется интерпретацией, если для любых формул А и В исчисления

высказываний h удовлетворяет следующим условиям
Слайд 8Истинность и ложность
Формула А исчисления высказываний истинна при некоторой интерпретации h тогда

и только тогда, когда h(A)=1
В противном случае, говорят, что А ложна при интерпретации h
Слайд 9Тавтология и противоречие
Формула А исчисления высказываний является тавтологией, тогда и только тогда,

когда она истинна независимо от интерпретации
Формула А называется противоречием, тогда и только тогда, когда она ложна при любой интерпретации
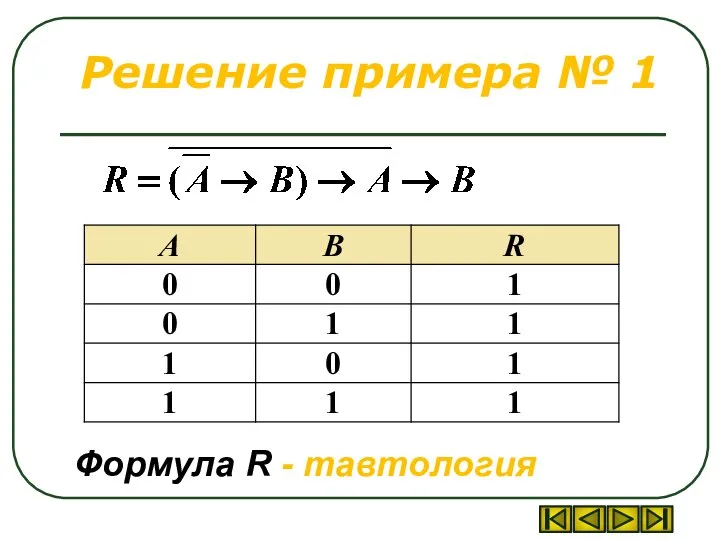
Слайд 10Пример № 1
Проверить, что формула R является тавтологией

Слайд 11Решение примера № 1
Формула R - тавтология
Слайд 12Правило подстановки
Пусть А – некая формула, выводимая (доказуемая) в исчислении высказываний, х-

переменная,
В – любая формула исчисления высказываний
Тогда формула, которая получается из формулы А путем подстановки в нее вместо переменной х формулы В, выводима (доказуема)
А(……х…..)(B//x)
Слайд 13Пример № 2
Проверить, что формула А→А выводима в исчислении высказываний

Слайд 14Решение примера № 2
1. Подставим в аксиому А2 вместо В (А→А), вместо

С подставим А
2. Применив аксиому А1, и по правилу заключения получаем
3. Применив аксиому А1 и по правилу заключения получаем
Слайд 15Теорема
Каждая формула, доказуемая в исчислении высказываний, тождественно истинна в алгебре высказываний

Слайд 16Пример № 3
Каждая аксиома – тождественно истинная
Правило подстановки, примененное к

тождественно истинным формулам, приводит к тождественно истинным формулам
Правило заключения, примененное к тождественно истинным формулам, приводит к тождественно истинным формулам
Слайд 17Теорема дедукции
Если Г – множество формул,
А и В – формулы из Г

высказываний, и А├В, то Г├А→В, т.е. в Г выводима формула А→В
Слайд 18Пример № 4
Проверить, что из А→В, В→С формула А→С выводима в

исчислении высказываний, т.е. А→В, В→С ├ А→С
Слайд 19Решение примера № 4
А→В –гипотеза
В→С - гипотеза
А -

тоже гипотеза
В выводимо по правилу заключения из п. 1 и п. 3
С выводимо по правилу заключения из п. 2 и п. 4
Следовательно, А→В, В→С А├С, и , по теореме о дедукции, А→В, В→С ├А→С
Слайд 20Разрешимость и независимость
Проблема разрешимости для исчисления высказываний разрешима
Система аксиом исчисления высказываний независима

Слайд 21Полнота и непротиворечивость
Исчисление высказываний полно в узком смысле, т.е. к системе аксиом

нельзя добавить в качестве новой аксиомы недоказуемой в этом исчислении формулы
Исчисление высказываний полно в широком смысле, т.е. всякая тождественно истинная формула алгебры высказываний доказуема в исчислении высказываний
Исчисление высказываний непротиворечиво
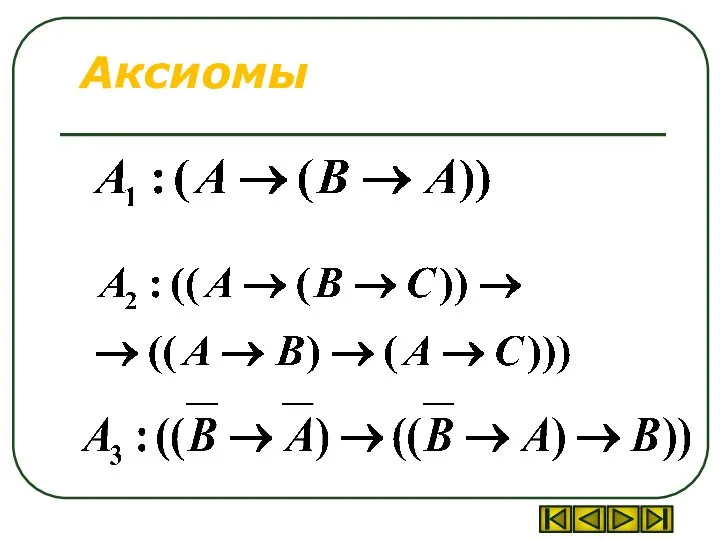
Слайд 22Исчисление высказываний по Гильберту и Аккерману
Связки
Аксиомы
Правило вывода МР





















 Дискретная математика с элементами математической логики. Основы теории множеств
Дискретная математика с элементами математической логики. Основы теории множеств Числовая окружность в координатной плоскости
Числовая окружность в координатной плоскости 21baz
21baz Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Деление (урок по математике для 2 класса по учебнику Петерсон Л.Г.)
Деление (урок по математике для 2 класса по учебнику Петерсон Л.Г.) Логарифмические уравнения
Логарифмические уравнения Параллельные прямые в пространстве
Параллельные прямые в пространстве Презентация на тему Подобие треугольников
Презентация на тему Подобие треугольников  Правильные многогранники
Правильные многогранники Первый признак подобия треугольников. Решение задач
Первый признак подобия треугольников. Решение задач Тренажёр. Таблица умножения. Юные водители
Тренажёр. Таблица умножения. Юные водители Предмет стереометрии. Аксиомы стереометрии
Предмет стереометрии. Аксиомы стереометрии Вычисление интегралов вида R(x, Jax2 + bx+c) dx
Вычисление интегралов вида R(x, Jax2 + bx+c) dx Сводка и группировка
Сводка и группировка Решение задач и уравнений
Решение задач и уравнений Задачи на увеличение (уменьшение) числа на несколько единиц
Задачи на увеличение (уменьшение) числа на несколько единиц Математика. 1 класс
Математика. 1 класс Какую прямую называют координатной?
Какую прямую называют координатной? Математический диктант по теме: Дроби. 6 класс
Математический диктант по теме: Дроби. 6 класс Шестое математическое действие
Шестое математическое действие Анализ и синтез. 58-59-60 Урок
Анализ и синтез. 58-59-60 Урок Преобразования неравенств
Преобразования неравенств Многогранники, символы красоты и совершенства
Многогранники, символы красоты и совершенства Неравенства системы и совокупности неравенств
Неравенства системы и совокупности неравенств Обыкновенные дроби. Эти таежные животные
Обыкновенные дроби. Эти таежные животные Обозначение геометрических фигур буквами
Обозначение геометрических фигур буквами B7
B7 Игровой тренажер
Игровой тренажер