Содержание
- 2. Опр.: Левая Правая полуокрестность числа а - это всякий интервал , имеющий число а своим правым
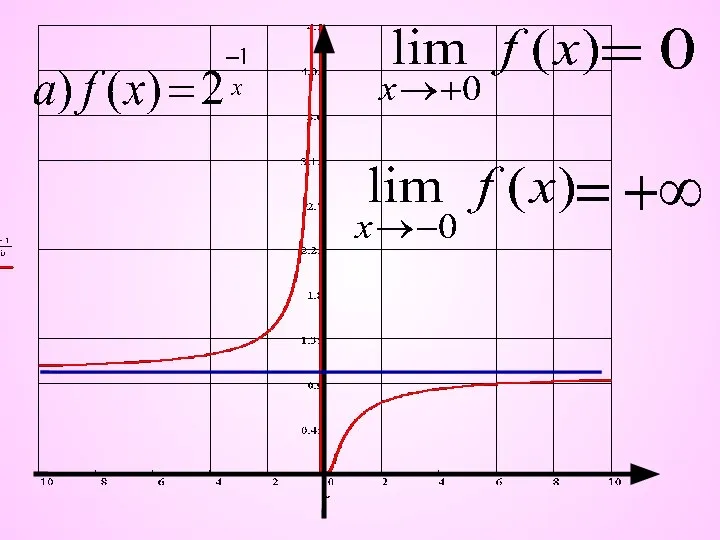
- 3. Опр.: Функция f(x) имеет правый левый предел в точке а, если из того, что ,оставаясь в
- 6. Опр.: Если существуют правый и левый пределы функции в точке a и они равны одному и
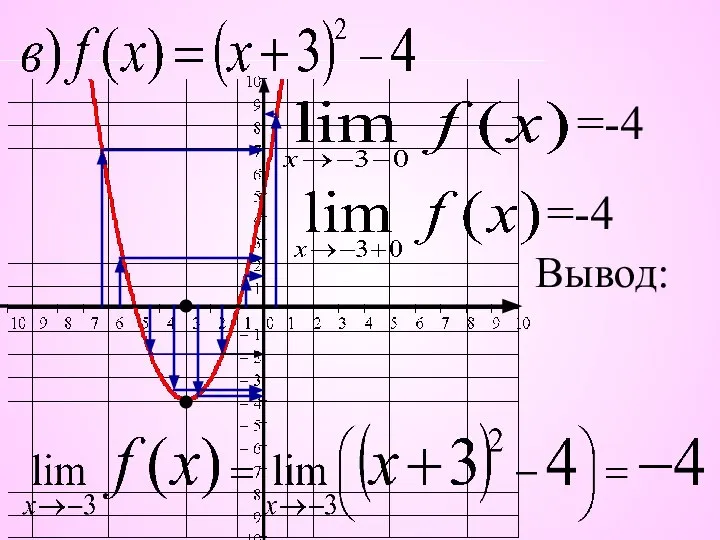
- 7. =-4 =-4 Вывод:
- 9. Опр.: Точка а называется точкой разрыва функции f(x), если 1) точка а является точкой прикосновения для
- 10. Классификация точек разрыва. 1) Точка а называется точкой разрыва I рода (скачок), если функция в этой
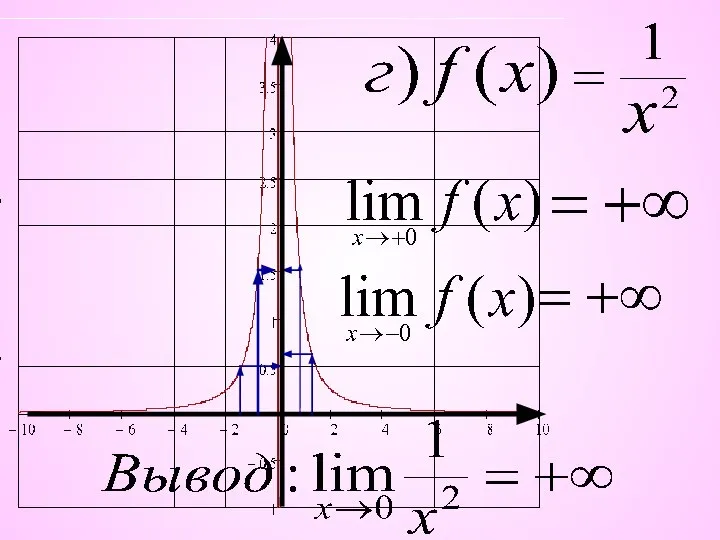
- 11. 2) Точка а называется точкой разрыва II рода , если хотя бы один из односторонних пределов
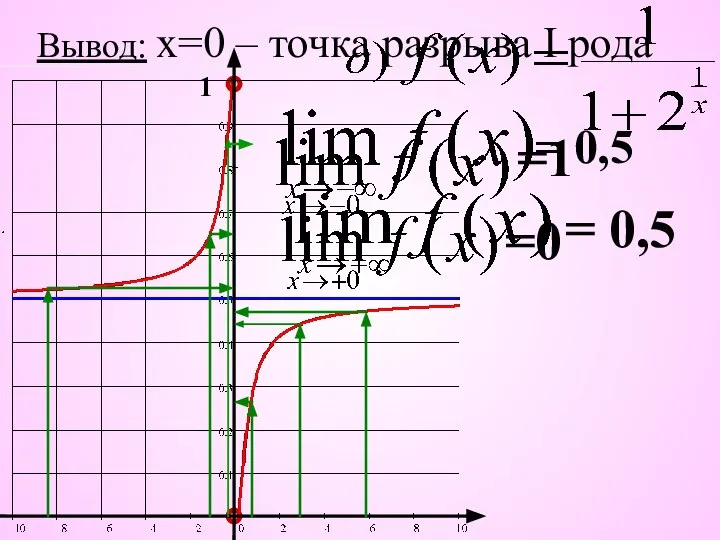
- 12. =0 1 =1 Вывод: х=0 – точка разрыва I рода = 0,5 = 0,5
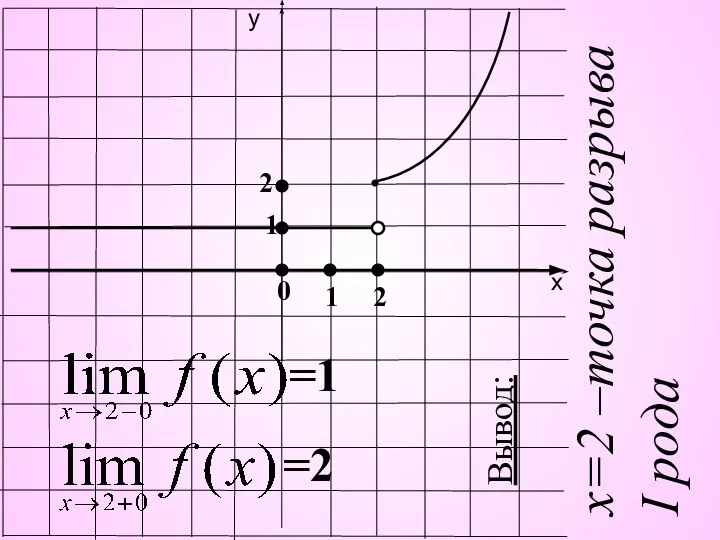
- 13. =1 =2 0 1 1 2 2 Вывод: х=2 –точка разрыва I рода
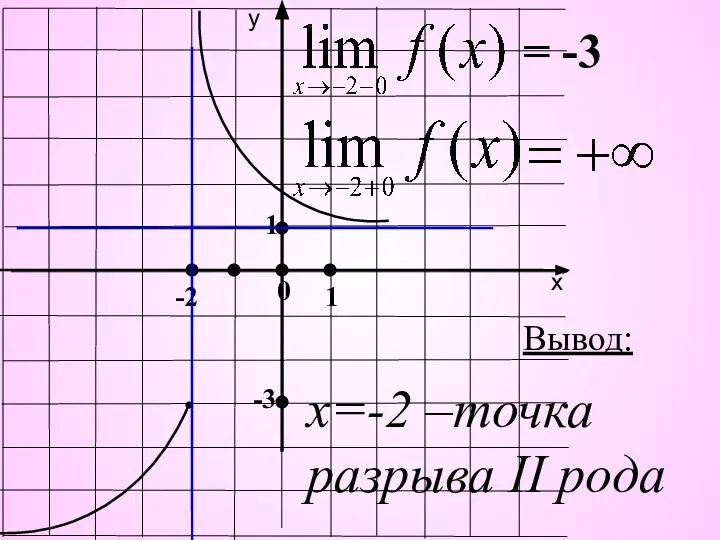
- 14. 0 1 1 -2 -3 Вывод: х=-2 –точка разрыва II рода = -3
- 17. Скачать презентацию







 Реши задачу
Реши задачу Аксиомы стереометрии. Некоторые следствия из аксиом
Аксиомы стереометрии. Некоторые следствия из аксиом В путешествие пойдём. В страну чисел попадём
В путешествие пойдём. В страну чисел попадём Функции, их свойства и графики
Функции, их свойства и графики Решение задач и примеров на сложение в пределах 1000 с переходом через разряд
Решение задач и примеров на сложение в пределах 1000 с переходом через разряд Физкультминутка. Таблица перевода мер длин
Физкультминутка. Таблица перевода мер длин Презентация на тему Умножение многочленов (7 класс)
Презентация на тему Умножение многочленов (7 класс)  Почему нельзя делить на ноль
Почему нельзя делить на ноль Ортогональная проекция плоской фигуры на плоскость и ее площадь
Ортогональная проекция плоской фигуры на плоскость и ее площадь Формулы понижения степени числа
Формулы понижения степени числа Интерактивная игра. Математический футбол
Интерактивная игра. Математический футбол Готовимся к ЕГЭ
Готовимся к ЕГЭ Презентация на тему Наибольшее и наименьшее значения функции
Презентация на тему Наибольшее и наименьшее значения функции  Теорема об интегрировании рядов Фурье
Теорема об интегрировании рядов Фурье Линейная функция и её график
Линейная функция и её график Системы координат, используемые в спутниковых измерениях
Системы координат, используемые в спутниковых измерениях Многогранники. Единица объема. Объем прямоугольного параллелепипеда
Многогранники. Единица объема. Объем прямоугольного параллелепипеда Сложение и вычитание трехзначных чисел
Сложение и вычитание трехзначных чисел Векторы в пространстве
Векторы в пространстве Доказательство тождеств, содержащих многочлен
Доказательство тождеств, содержащих многочлен ЛЕКЦИЯ_7
ЛЕКЦИЯ_7 Свойства функции. Для повторения
Свойства функции. Для повторения Анализ и изображение пространственных фигур
Анализ и изображение пространственных фигур Решение квадратных уравнений выделением квадрата двучлена
Решение квадратных уравнений выделением квадрата двучлена Презентация на тему Функция. График функции.
Презентация на тему Функция. График функции.  Икосаэдр
Икосаэдр Элементы линейной алгебры. Матрицы. Определители
Элементы линейной алгебры. Матрицы. Определители Сумма углов треугольника
Сумма углов треугольника