1_1_matritsy (1)

1. МАТРИЦЫ
И
ОПРЕДЕЛИТЕЛИ

1.1. МАТРИЦЫ И ДЕЙСТВИЯ
НАД НИМИ
Матрицей размера m x n называется
прямоугольная таблица чисел,
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.

Обозначение:
Где
i=1,2…m
j=1,2…n
- матрица размерности m x n
- элемент матрицы i –ой строки и j -го столбца

матрица размерности m x n

Две матрицы называются равными, если
у них одинаковая размерность и
совпадают строки и столбцы.
Если число строк матрицы равно числу ее
столбцов, то такая матрица называется
квадратной.

Пример:
- квадратная матрица размерности 3х3

Элементы матрицы aij , у которых номер
столбца совпадает с номером строки,
называются диагональными.
Если в квадратной матрице все
диагональные элементы равны 1, а
остальные элементы равны 0, то
она называется единичной.

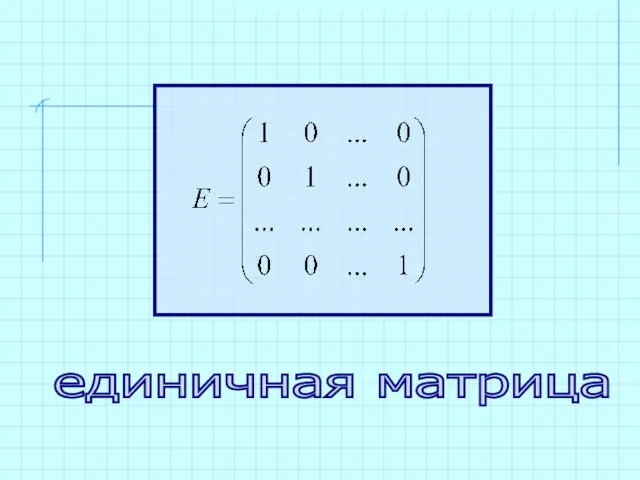
единичная матрица

Матрица любого размера называется
нулевой, если все ее элементы равны 0.
нулевая матрица

Матрица, состоящая из одной строки,
называется матрицей-строкой или
вектором-строкой.
матрица-строка

Матрица, состоящая из одного столбца,
называется матрицей-столбцом или
вектором-столбцом.
матрица-столбец

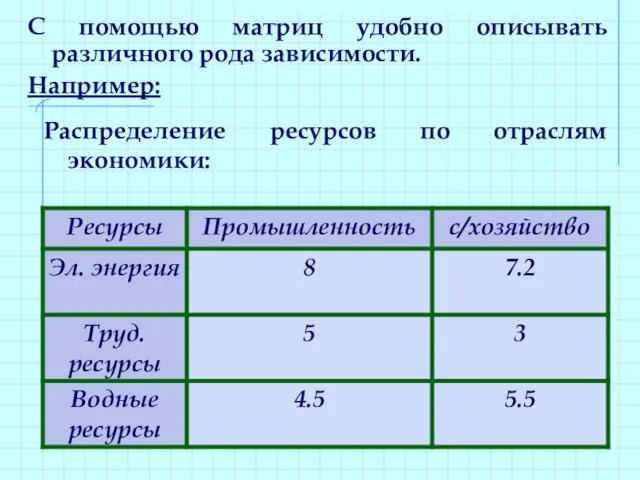
Распределение ресурсов по отраслям экономики:
С помощью матриц удобно описывать различного рода зависимости.
Например:

Эту зависимость можно представить в виде матрицы:
Где элемент aij показывает сколько i – го ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды потребляет сельское хозяйство.

ДЕЙСТВИЯ НАД МАТРИЦАМИ
1. Умножение матрицы на число
Чтобы умножить матрицу на число, надо
каждый элемент матрицы умножить на
это число.
Полученные произведения образуют итоговую матрицу.

Пусть дана матрица
Умножаем ее на число λ:
Где каждый элемент матрицы В:
Где:

Например:
Умножая матрицу
на число 2, получим:

2. Сложение матриц
Складываются матрицы одинаковой
размерности. Получается матрица той же
размерности, каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.

Пусть даны матрицы
Складываем их:
Где каждый элемент матрицы С:
Аналогично проводится вычитание матриц.

Пример.
Найти сумму и разность матриц:

Решение:

3. Умножение матриц
Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй.
Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j-го столбца второй.

Пусть даны матрицы
Умножаем их:
Где каждый элемент матрицы С:

Пример.
Найти произведение матриц:

Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует:
Решение:

Теперь перемножим матрицы в обратном порядке:
Умножение матриц в общем случае некоммутативно:

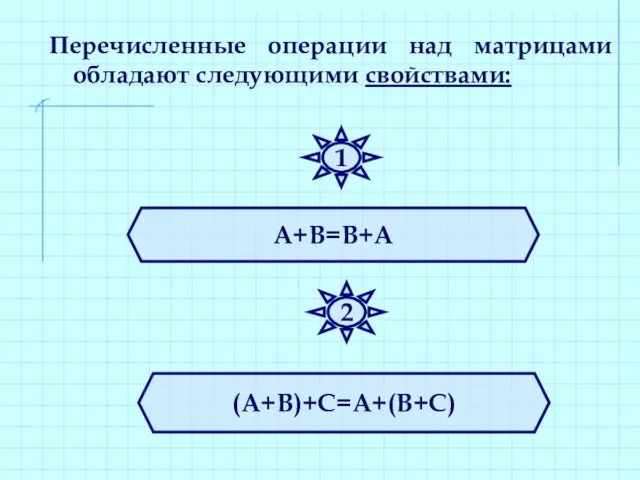
Перечисленные операции над матрицами обладают следующими свойствами:
А+В=В+А
(А+В)+С=А+(В+С)
1
2

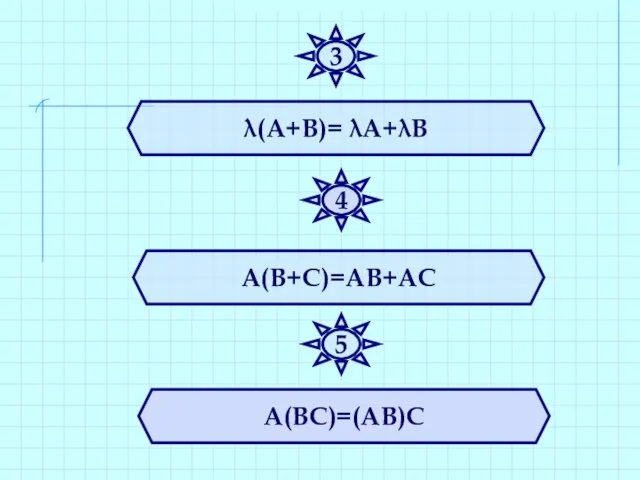
λ(А+В)= λА+λВ
А(В+С)=АВ+АС
А(ВС)=(АВ)С
3
4
5

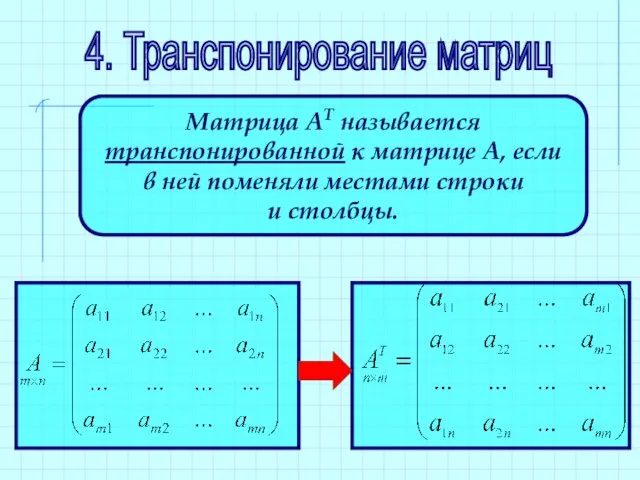
4. Транспонирование матриц
Матрица АТ называется
транспонированной к матрице А, если
в ней поменяли местами строки
и столбцы.

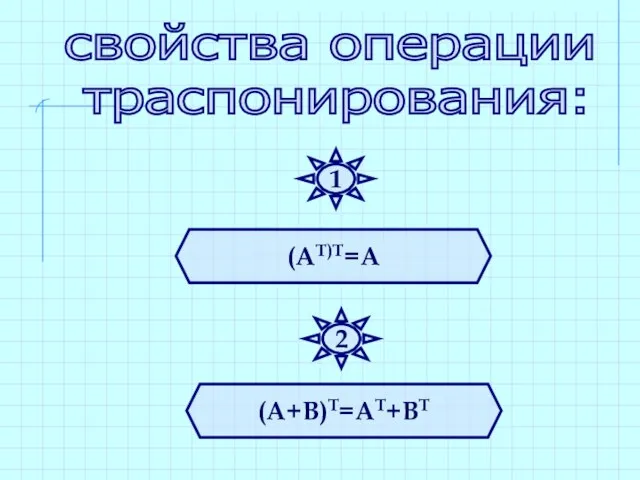
(АТ)Т=А
(А+В)Т=АТ+ВТ
свойства операции траспонирования:
1
2

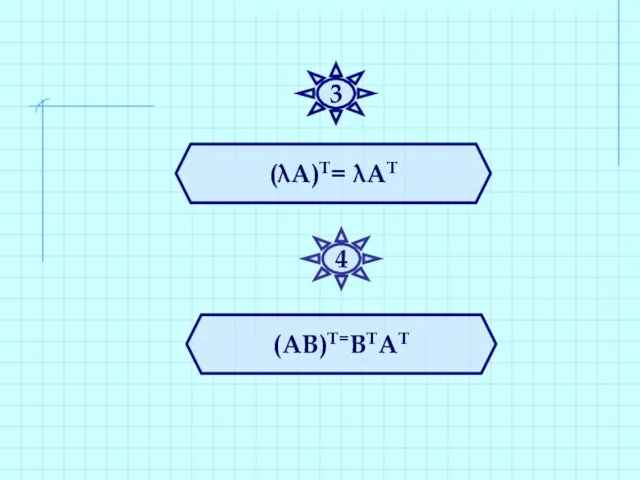
(λА)Т= λАТ
(АВ)Т=ВТАТ
3
4

Пример.
Транспонировать матрицу: