Содержание
- 2. Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Х - число очков,
- 3. Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все возможные значения можно пронумеровать
- 4. Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет собой таблицу, в которой указаны
- 6. ПРИМЕР. Игральный кубик бросается 1 раз. Пусть случайная величина Х - число выпавших очков. Составим для
- 7. ПРИМЕР. Игральный кубик бросается 1 раз. Пусть случайная величина Х - число выпавших очков. Составим для
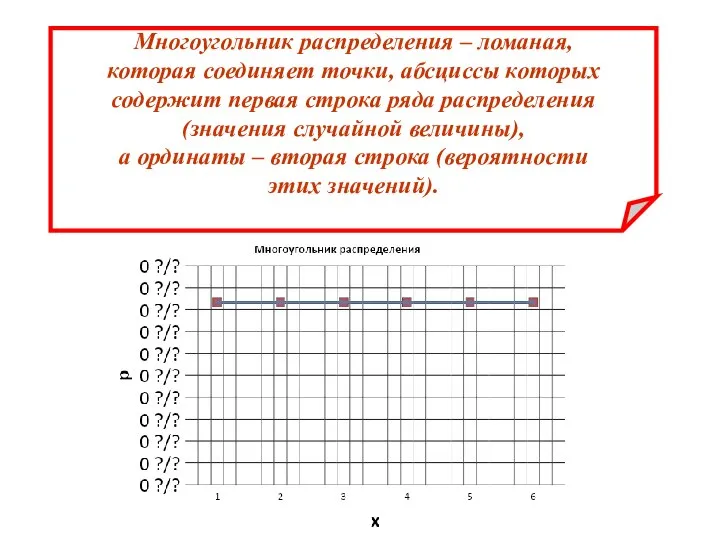
- 8. Многоугольник распределения – ломаная, которая соединяет точки, абсциссы которых содержит первая строка ряда распределения (значения случайной
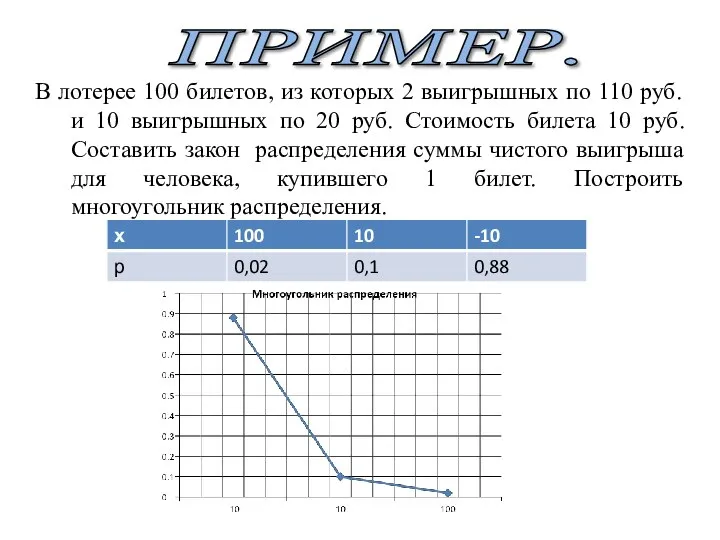
- 9. ПРИМЕР. В лотерее 100 билетов, из которых 2 выигрышных по 110 руб. и 10 выигрышных по
- 10. ПРИМЕР. В лотерее 100 билетов, из которых 2 выигрышных по 110 руб. и 10 выигрышных по
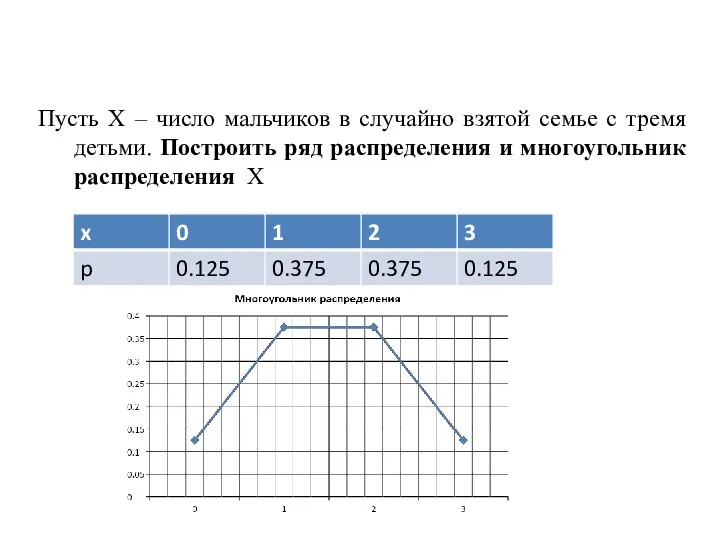
- 11. ПРИМЕР. Пусть Х – число мальчиков в случайно взятой семье с тремя детьми. Построить ряд распределения
- 12. ПРИМЕР. Пусть Х – число мальчиков в случайно взятой семье с тремя детьми. Построить ряд распределения
- 13. ПРИМЕР. Пусть Х – число мальчиков в случайно взятой семье с тремя детьми. Построить ряд распределения
- 14. ПРИМЕР. Пусть Х – число мальчиков в случайно взятой семье с тремя детьми. Построить ряд распределения
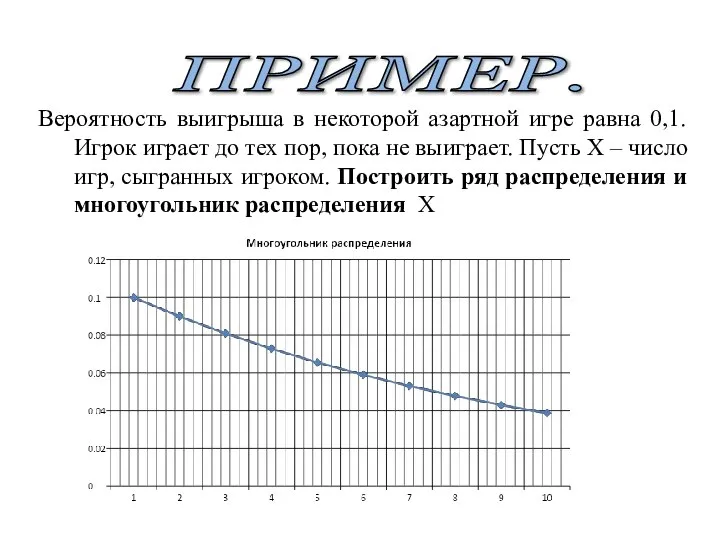
- 15. ПРИМЕР. Вероятность выигрыша в некоторой азартной игре равна 0,1. Игрок играет до тех пор, пока не
- 16. ПРИМЕР. Вероятность выигрыша в некоторой азартной игре равна 0,1. Игрок играет до тех пор, пока не
- 17. ПРИМЕР. Вероятность выигрыша в некоторой азартной игре равна 0,1. Игрок играет до тех пор, пока не
- 18. ПРИМЕР. Вероятность выигрыша в некоторой азартной игре равна 0,1. Игрок играет до тех пор, пока не
- 20. Скачать презентацию













 Периметр прямоугольника
Периметр прямоугольника user_file_54317c3324dbe (1)
user_file_54317c3324dbe (1) Треугольники и не только они
Треугольники и не только они Презентация на тему Перпендикулярные прямые (7 класс)
Презентация на тему Перпендикулярные прямые (7 класс)  Уравнение Бернулли
Уравнение Бернулли Устный счет
Устный счет Обыкновенная дробь
Обыкновенная дробь Презентация на тему График квадратичной функции Неравенства с одной переменной
Презентация на тему График квадратичной функции Неравенства с одной переменной  برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد
برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد История симметрии
История симметрии Сложение дробей с один знаменателем
Сложение дробей с один знаменателем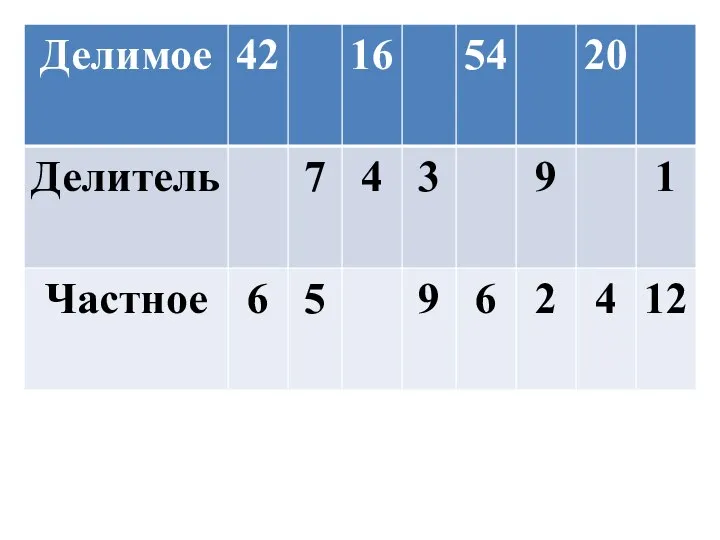 Таблица умножения и деления
Таблица умножения и деления Параллельные прямые
Параллельные прямые Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни
Задачи на движение. Нахождение времени. Взаимосвязь между величинами: скорость, время, расстояни Урок повторения
Урок повторения Квадратичная функция. Решение текстовых задач
Квадратичная функция. Решение текстовых задач Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7
Математический тренажёр Наряжаем ёлочку. Случаи сложения и вычитания вида 26+4, 30-7 Вычисление длины дуги
Вычисление длины дуги Длина окружности
Длина окружности Решение задач по теории вероятности. Подготовка к ГИА
Решение задач по теории вероятности. Подготовка к ГИА Определители матриц
Определители матриц Формулы. Уравнение
Формулы. Уравнение Выполни карточки от учителя на УЧИ.ру
Выполни карточки от учителя на УЧИ.ру Средняя квадратическая величина
Средняя квадратическая величина Понятие производной
Понятие производной Показательная функция
Показательная функция Тетраэдр и параллелепипед
Тетраэдр и параллелепипед Арифметический корень натуральной степени
Арифметический корень натуральной степени