Алгебра и начала математического анализа, 11 класс

Мы знаем, как решать логарифмические уравнения, сегодня мы научимся решать логарифмические неравенства, не трудно догадаться, что они имеют вот такой вид:
Давайте, преобразуем наше неравенство и разберемся, как решать его.

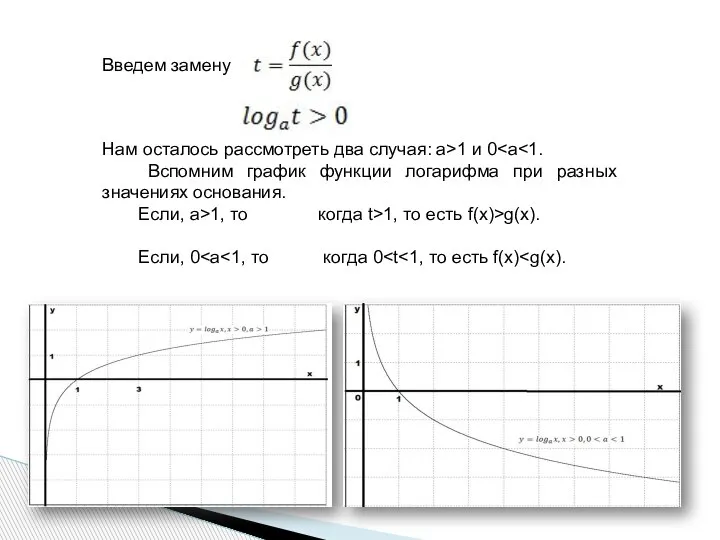
Введем замену
Нам осталось рассмотреть два случая: а>1 и 0
Вспомним график функции логарифма при разных значениях основания.
Если, а>1, то когда t>1, то есть f(x)>g(x).
Если, 0

Давайте сформулируем основное правило при решении логарифмических неравенств:
Если f(x)>0 и g(x)>0, то:
Так же при решении логарифмических неравенств следует помнить о том, что выражения стоящие под знаком логарифма строго положительные, тогда неравенство обычно преобразует вот к такой системе неравенств.

Алгоритм решения логарифмических неравенств.

Пример. Решить неравенство
Решение.
Основание логарифма равно 4, что больше одного, тогда наше неравенство равносильно системе:
Построим наши промежутки на рисунке и найдем их пересечение:
Ответ: xϵ(-3;1)

Пример. Решить неравенство
Решение.
Основание логарифма, в нашем примере, меньше единицы, переходим к неравенству противоположного смысла, тогда логарифмическое неравенство равносильно системе неравенств:
В нашем случае можно не строить рисунок с промежутками, очевидно, что x>1.
Ответ: x>1

Пример. Решить неравенство
Решение.
Поработаем с правой частью неравенства, представим число -2 в виде логарифма с основанием одной пятой.
И так
Основание логарифма меньше единицы, переходим к неравенству противоположному по смыслу
Обратим внимание, на то, что первое неравенство системы мы можем не решать, так как в левой части, обоих неравенств, у нас стоят одинаковые выражения, а в правой положительные числа. Проще говоря, если А≥25, то очевидно А>0.

Решим неравенство
Построим промежуток
Ответ: xϵ[0;5]

Пример. Решить неравенство
Решение.
Рассмотрим левую часть неравенства:
Рассмотрим правую часть неравенства:
Исходное неравенство равносильно неравенству:
Основание логарифма больше единицы, тогда мы можем перейти к неравенству того же знака и нам останется решить систему:
Графически найдем решение
Ответ: xϵ[1;6].

Пример. Решить неравенство
Решение.
Посмотрим внимательно на выражение:
Воспользуемся методом замены переменных.
Пусть
Наше неравенство примет вид
Решением нашего неравенства будет промежуток:
Введем обратную замену
Ответ: