2_бинарные отношения

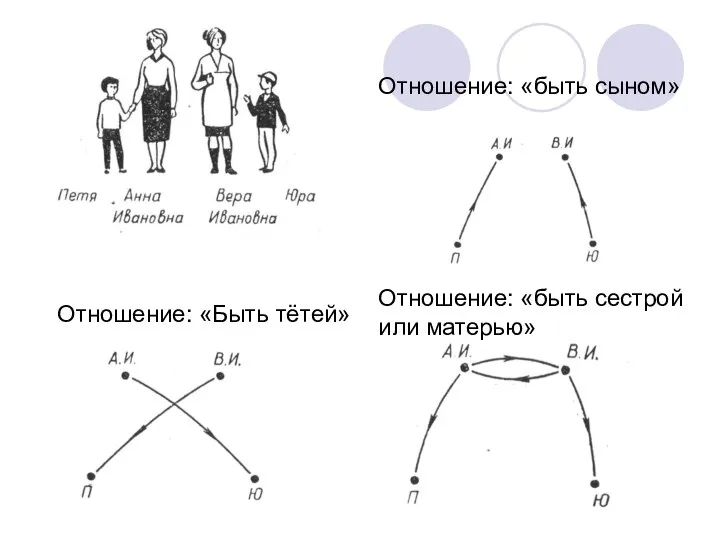
Отношение: «быть сыном»
Отношение: «Быть тётей»
Отношение: «быть сестрой или матерью»

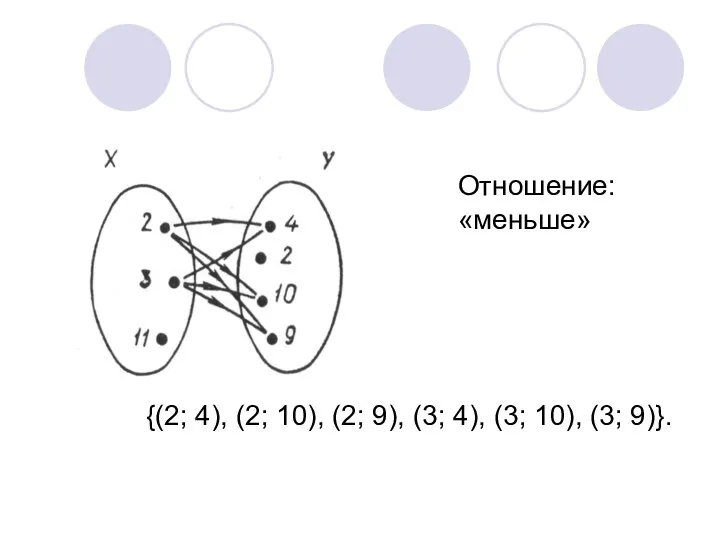
Отношение: «меньше»
{(2; 4), (2; 10), (2; 9), (3; 4), (3; 10), (3; 9)}.

Прямым (декартовым) произведением множеств А и В называется множество всех пар (а,b), таких, что а∈А и b∈В.
Прямое произведение множеств А и В обозначается в виде А×В:
А×В = {(a, b)⏐a∈A и b∈B}.
Пример: Х – множество точек отрезка [0;1];
Y – множество точек отрезка [1;2].
Тогда ХхY – множество точек квадрата с вершинами в точках (0,1), (0,2), (1,1), (1,2).
Прямое (декартово) произведение одинаковых множеств называется декартовой степенью множества:
если В = А, то АхВ = АхА = А2.

n-местным (n-арным) отношением R заданным на множествах М1, М2,…Мn называется подмножество R декартова произведения этих множеств
R ⊆ М1хМ2х…хМn , где
m1∈М1, m2∈М2,…mn∈Мn и
n-ки элементов (m1, m2 ,…mn)∈ R
При n=2 отношение между элементами двух множеств есть множество пар (m1, m2)
Отношение

Бинарные отношения
Бинарным отношением между элементами множеств А и В называется любое подмножество R⊆A×B.
Если множества A и B совпадают А=В, то R называют бинарным отношением на множестве А. (однородное отношение)
Если (x, y)∈R, то это обозначают еще xRy и говорят, что между элементами x и y установлено бинарное отношение R.

Примеры
Отношение a= {(4, 4), (3, 3), (2, 2), (4, 2)} на множестве X = {4, 3, 2} можно определить как свойство "Делится" на этом подмножестве целых чисел.
Из школьного курса
На множестве целых чисел Z отношения "делится", "делит", "равно", "больше", "меньше";
на множестве прямых пространства отношения "параллельны", "взаимно перпендикулярны", "скрещиваются", "пересекаются", "совпадают";
на множестве окружностей плоскости "пересекаются", "касаются", "концентричны".

Пример
Пусть A=B R, пара (x, y) является точкой вещественной плоскости. Тогда:
Бинарное отношение
R1 = { (x, y) | x2 + y2 ≤1 }
определяет замкнутый круг единичного радиуса с центром в точке (0,0) на плоскости
Отношение
R2 = { (x, y) | x ≥ y }
полуплоскость
Отношение
R3= { (x, y) | |x-y| ≤ 1 }
полосу.

Способы задания
Перечисление всех пар из базового множества А и базового множества В
A={a1 ,a2} B={b1,b2,b3}, R={(a1, b1), (a1 ,b3), (a2, b1)}
Отношения могут задаваться формулами:
- Формулы y = x2 +5x - 6 или x + y < 5 задают бинарные отношения на множестве действительных чисел;
- формула x + y = любовь, задает бинарное отношение на множестве людей.

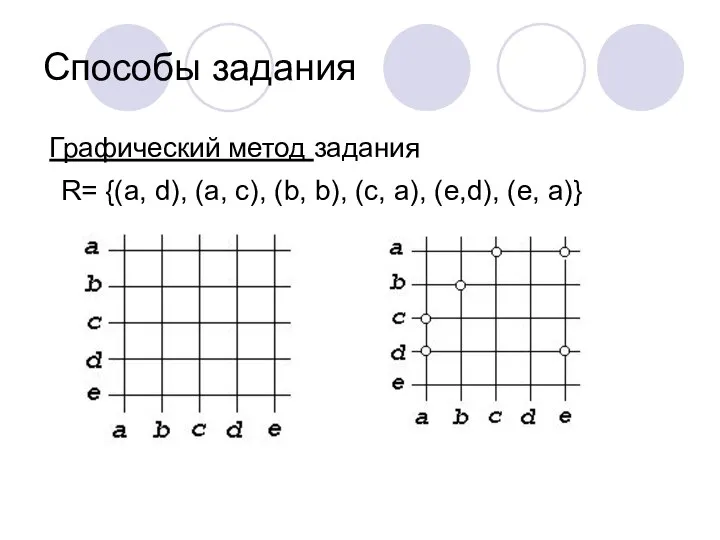
Графический метод задания
R= {(a, d), (a, c), (b, b), (c, a), (e,d), (e, a)}
Способы задания

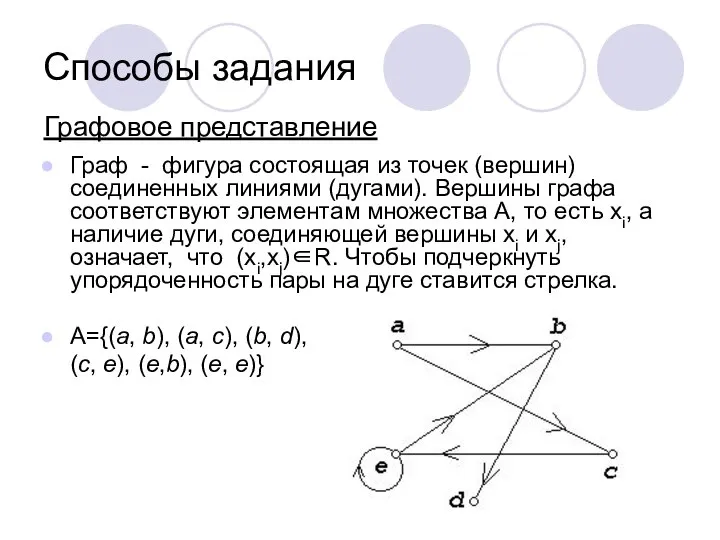
Графовое представление
Граф - фигура состоящая из точек (вершин) соединенных линиями (дугами). Вершины графа соответствуют элементам множества А, то есть xi, а наличие дуги, соединяющей вершины xi и xj, означает, что (xi,xj)∈R. Чтобы подчеркнуть упорядоченность пары на дуге ставится стрелка.
А={(a, b), (a, c), (b, d),
(c, e), (e,b), (e, e)}
Способы задания

Матричная форма задания
Пусть на некотором конечном множестве X задано отношение А. Упорядочим каким-либо образом элементы множества X = {x1, x2, ..., xn} и определим матрицу отношения A = [aij] следующим образом:
Способы задания

Определения
Диагональ множества A×A, т.е. множество
Δ={(x,x) | x∈A},
называется единичным бинарным отношением или отношением равенства в A.
Областью определения бинарного отношения R называется множество
δR={ x∈A | y∈B, (x, y) ∈R }.
Областью значений бинарного отношения R называется множество
ρR={ y∈B | x∈A, (x, y)∈R }.

Операции над бинарными отношениями
Пересечение двух бинарных отношений R1 и R2 - это отношение
R1∩R2 = { (x, y) | (x, y)∈R1 и (x, y)∈R2 }.
≥ ∩ ≠ = >
Объединение двух бинарных отношений R1 и R2 - это отношение
R1∪R2 = { (x, y) | (x, y)∈R1 или (x, y)∈R2 }.
Разностью отношений R1 и R2 называется такое отношение, что:
R1\R2 = { (x, y) | (x, y)∈R1 и (x, y)∉R2 }
Дополнение к отношению
R={ (x, y) | (x, y)∈(A×A)\R}.

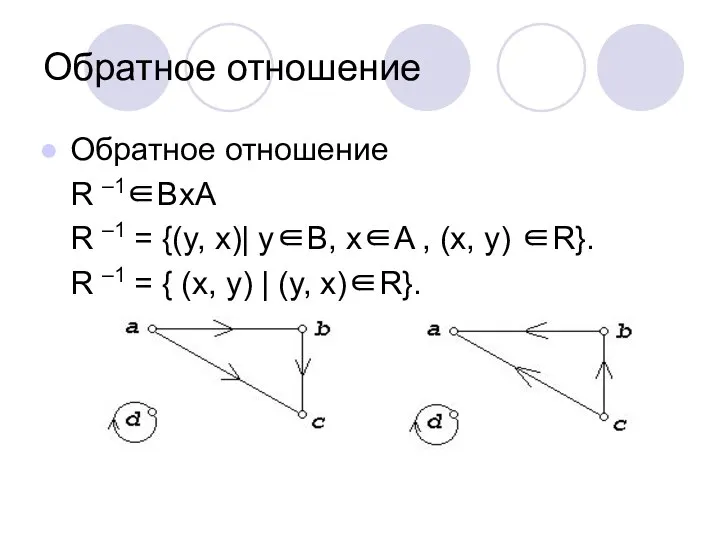
Обратное отношение
Обратное отношение
R –1∈BxA
R –1 = {(y, x)| y∈B, x∈A , (x, y) ∈R}.
R –1 = { (x, y) | (y, x)∈R}.

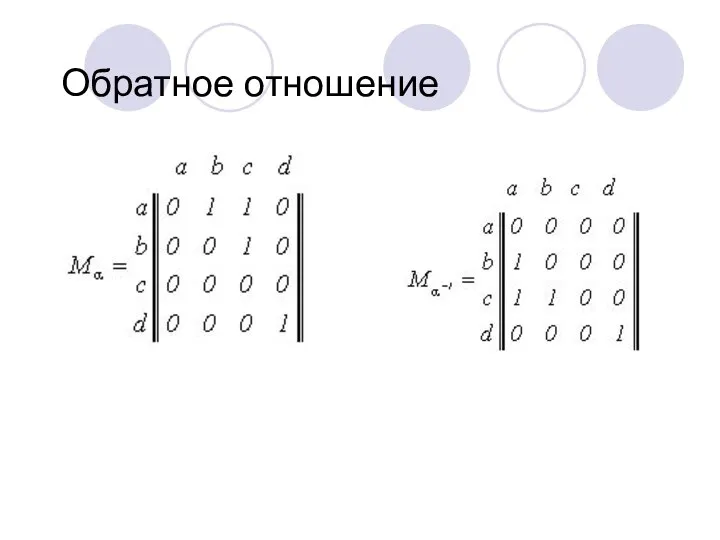
Обратное отношение

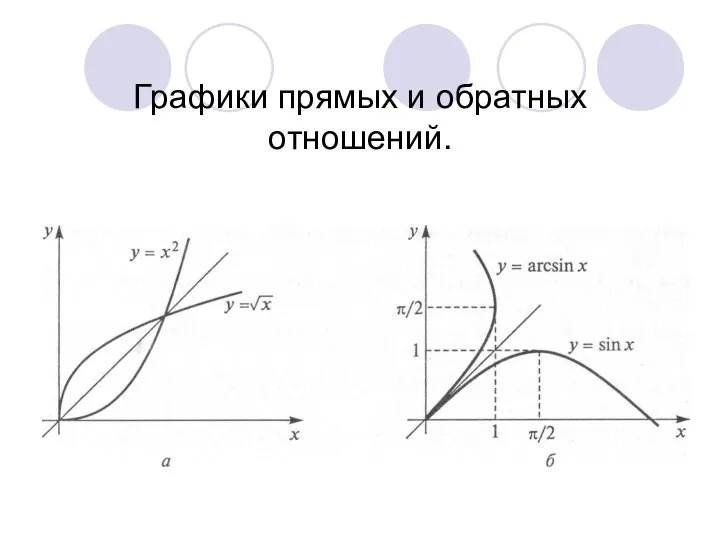
Графики прямых и обратных отношений.

Композиция отношений
Композиция (суперпозиция) отношений R=R1oR2 содержит пару (x, y) тогда и только тогда, когда существует такое z∈A, что
(x, z)∈R1 и (z, y)∈R2.

Свойства отношений
R1 содержится в R2 (R1 ⊆ R2), если любая пара (x, y), которая принадлежит отношению R1 также принадлежит и отношению R2
Рефлексивность
∀x∈M (xRx)
Антирефлексивность
∀x∈M ¬(xRx)

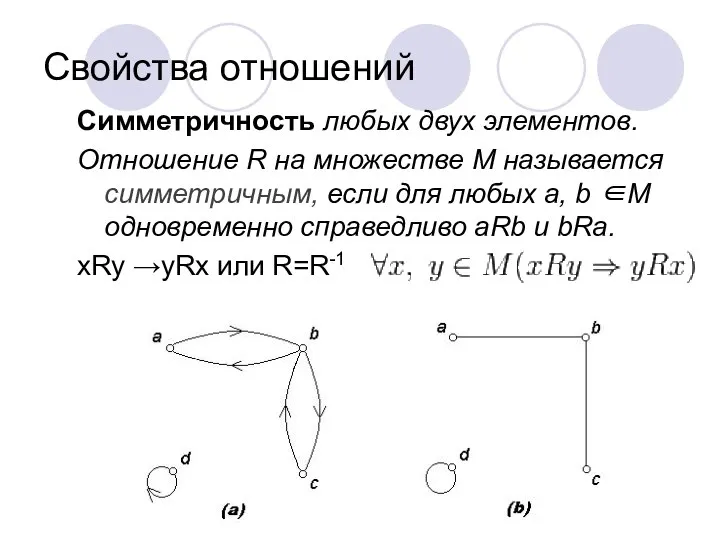
Свойства отношений
Симметричность любых двух элементов.
Отношение R на множестве М называется симметричным, если для любых a, b ∈М одновременно справедливо aRb и bRa.
xRy →yRx или R=R-1

Свойства отношений
Антисимметричность
Пусть А - множество людей в данной очереди. Отношение R "не стоять за кем-то в очереди" будет антисимметричным.
Пусть х=ВАСЯ, а y=ИВАНОВ. Тот факт, что (x, y)∈R означает, что "ВАСЯ не стоит в очереди за ИВАНОВЫМ", (y, x)∈R - "ИВАНОВ не стоит за ВАСЕЙ". Очевидно, что одновременное выполнение обоих включений может быть, только если ВАСЯ и есть ИВАНОВ, т.е. x = y.
Отношение "≥" также антисимметрично: если x≥y и y≥x, то x=y.
Асимметричность
Асимметричность эквивалентна одновременной антирефлексивности и антисимметричности отношения.

Свойства отношений
Для любого отношения R вводятся понятия симметричной части отношения
Rs = R ∩R-1
и асимметричной части отношения
Ra = R \ Rs.
Если отношение R симметрично, то R= Rs,
Если отношение R асимметрично, то R= Ra.
Примеры.
Если R - "≥", то R-1 - "≤", Rs - "=", Ra - ">".

Нетранзитивное отношение
Отношение R, определенное на некотором множестве и отличающееся тем, что для любых х, у, z этого множества из xRy и yRz не следует xRz.
Примеры нетранзитивных отношений:
1.«x отец y»
2. "≠". Пусть x=2, y=3, z=2, тогда справедливо x≠y и y≠z, но x=z, т.е. (x, z)∉R.
Свойства отношений
Транзитивность отношений
Если aRb и bRc, то aRc для любых а, b, с ∈М.

Отношения эквивалентности
(подобия, равносильности)
Бинарное отношение R на множестве A называется отношением эквивалентности, если оно обладает следующими свойствами:
рефлексивность
симметричность
транзитивность
Обозначается =, ≈, ~, ≡

Отношение эквивалентности
х ≈ x для всех x∈A (рефлексивность)
Если x ≈ y, то y ≈ x (симметричность)
Если x ≈ y и y ≈ z, то x ≈ z (транзитивность)

Примеры
отношение параллельности на множестве прямых плоскости;
отношение подобия на множестве фигур плоскости;
отношение равносильности на множестве уравнений;
отношение "иметь одинаковые остатки при делении на фиксированное натуральное число m" на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают a≡b (mod m);
отношение "принадлежать одному виду" на множестве животных;
отношение "быть родственниками" на множестве людей;
отношение "быть одного роста" на множестве людей;
отношение "жить в одном доме" на множестве людей.

Классы эквивалентности
Система непустых подмножеств
{M1, M2, …}
множества M называется разбиением этого множества, если
M = M1∪M2∪ …
и при i≠j
Mi∩Mj =Ø.
Сами множества M1, M2, … называются при этом классами данного разбиения.

Примеры
Разложение всех многоугольников на группы по числу вершин - треугольники, четырехугольники, пятиугольники и т. д.;
Разбиение всех треугольников по свойствам углов (остроугольные, прямоугольные, тупоугольные);
Разбиение всех треугольников по свойствам сторон (разносторонние, равнобедренные, равносторонние);
Разбиение всех треугольников на классы подобных треугольников;
Разбиение множества всех учащихся данной школы по классам.

Класс эквивалентности
Классом эквивалентности C(a) элемента a называется подмножество элементов, эквивалентных a.
Из вышеприведённого определения немедленно следует, что, если и b∈C(a), то C(a) = C(b).

Теорема
Отношение эквивалентности, заданное между элементами базового множества Х, определяет разбиение множества Х на непересекающиеся классы эквивалентности базового множества

Теорема
Два класса эквивалентности либо совпадают, либо не пересекаются.
Доказательство. Пусть A и B - два класса эквивалентности из X. Допустим, что они пересекаются и c - общий элемент, то есть c ∈ A, c ∈ B. Если x - произвольный элемент из A, то x ~ c. Поскольку c ∈ B, то и x ∈ B. Таким образом, A ⊂ B. Аналогично доказывается, что B ⊂ A. Итак, A = B. Теорема доказана

Функция
Функцией называется бинарное отношение f из X в Y, если из (x,y)∈f и (x,z)∈f следует, что y=z. То есть каждому элементу x∈X соответствует не более одного элемента y∈Y.
Такое свойство отношения называется однозначностью, или функциональностью.