Содержание
- 2. Дисперсионный анализ Дисперсионный анализ (от латинского Dispersio – рассеивание / на английском Analysis Of Variance -
- 3. Проверка значимости оценок дисперсий проводиться по F-критерию Фишера: применяют для сравнения двух независимых нормально распределенных выборочных
- 4. Допущения в дисперсионном анализе: 1.случайные ошибки наблюдений имеют нормальное распределение; где и - математическое ожидание и
- 5. Факторы, рассматриваемые в дисперсионном анализе, бывают двух родов: 1) со случайными уровнями (выбор уровней производится из
- 6. Однофакторный дисперсионный анализ Задачей однофакторного дисперсионного анализа является изучение влияния одного фактора А (количественного или качественного),
- 7. где μ - суммарный эффект во всех опытах; di - эффект фактора А на i-м уровне
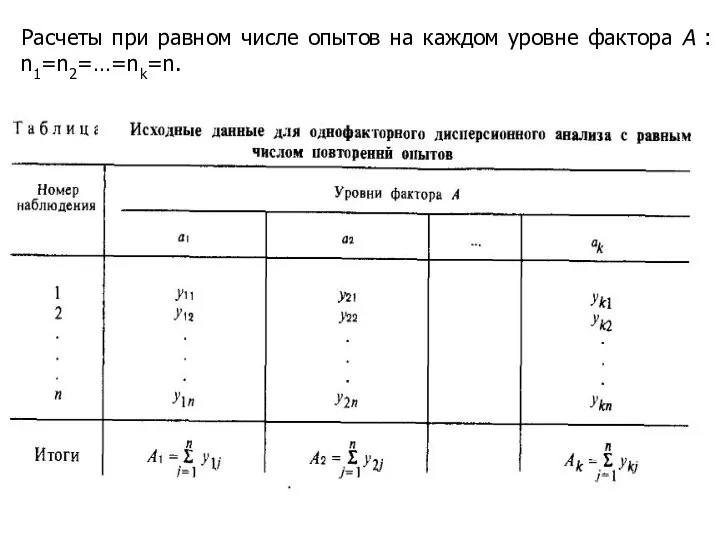
- 8. Расчеты при равном числе опытов на каждом уровне фактора А : n1=n2=…=nk=n.
- 9. Обозначим среднее значение наблюдений на i-том уровне: общее среднее значение для всей выборки из N наблюдений:
- 10. Определим выборочную дисперсию на каждом уровне: Критерий Кохрана (проверка однородности системы) применяют для сравнения k независимых
- 11. Если между выборочными дисперсиями нет значимых различий, для оценки генеральной дисперсии σ2 , характеризующей фактор случайности,
- 12. Введем следующее обозначение, дисперсия фактора А (проверка нулевой гипотезы по критерию Фишера): Влияние фактора является значимым,
- 13. Алгоритм: 1) итоги по столбцам 2) сумму квадратов всех наблюдений 3) сумму квадратов итогов по столбцам
- 14. 8) дисперсия 9) дисперсия 7) SSост - остаточная сумма квадратов для оценки ошибки эксперимента
- 15. Результаты расчета представляются в виде таблицы дисперсионного анализа. Если неравенство, справедливо, то различие между и значимо,
- 16. Если выборочные дисперсии различаются в пределах случайного разброса, то следующим шагом является сравнение выборочных средних. Выборочные
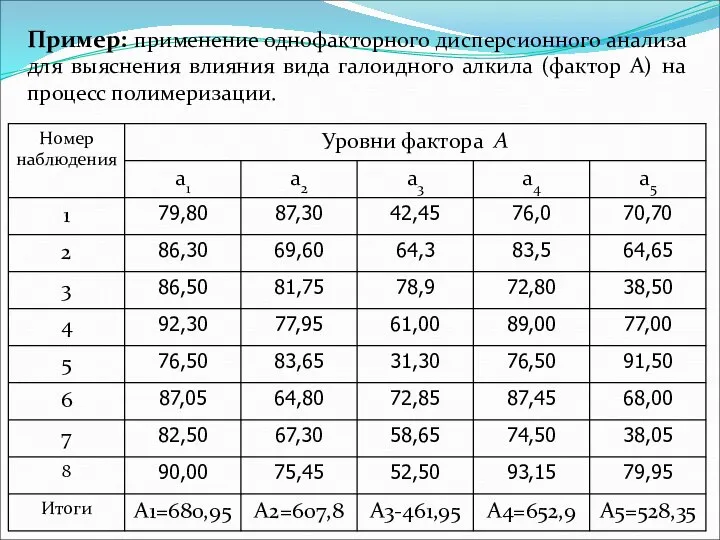
- 17. Пример: применение однофакторного дисперсионного анализа для выяснения влияния вида галоидного алкила (фактор А) на процесс полимеризации.
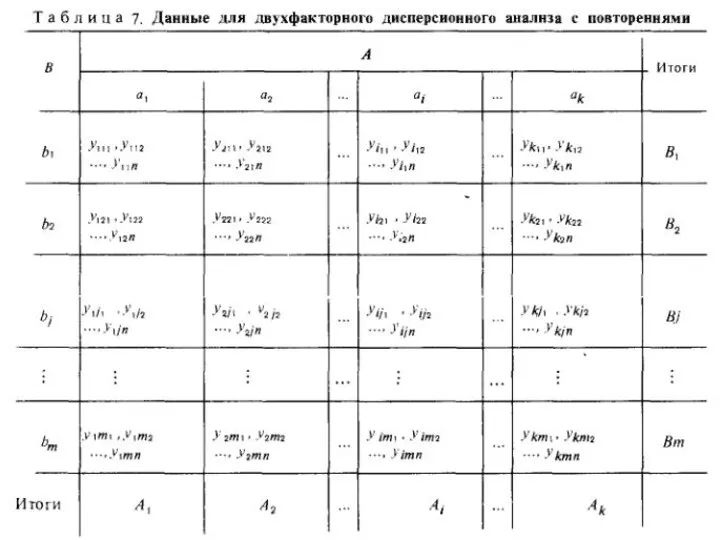
- 18. Двухфакторный дисперсионный анализ Изучается влияние на процесс одновременно двух факторов А и В. Фактор А исследуется
- 20. Общее число наблюдений равно N=nkm Общее среднее; эффект фактора А на i-м уровне, i=1,2,…, K; эффект
- 21. Если предположить, что между факторами нет взаимодействия, то можно использовать линейную модель:
- 22. Линейная модель: Через и обозначим соответственно средние значения по строкам и столбцам: А - среднее всех
- 23. В свою очередь, рассеяние в средних по строкам на зависит от фактора А и связано с
- 24. Эта дисперсия обусловлена влиянием фактора В и фактора случайности Вычитая (б) из (а), получим Отсюда Обозначим
- 25. Введем следующие обозначения: Величины и можно считать выборочными дисперсиями с (к-1) и (m-1) степенями свободы соответственно.
- 26. Если нулеваая гипотеза отвергается и влияние фактора А считается значимым. Аналогично, если Гипотеза принимается, βj =0.
- 27. При проведении дисперсионного анализа в условиях линейной модели, используют следующий алгоритм расчета: Находят : Итоги по
- 28. 5) Сумму квадратов итогов по строкам., деленную на число наблюдений в строке 6) Квадрат общего итога,
- 29. 11) Дисперсию : 12) Дисперсию : 13) Дисперсию :
- 31. Рассмотрим модель со взаимодействием факторов А и В. Пусть при каждом сочетании уровней факторов А и
- 32. Более удобная формула для вычисления дисперсии воспроизводимости где yij - сумма наблюдений в ij – й
- 33. При проведении дисперсионного анализа в условиях модели с учетом взаимодействия факторов А и В, удобно использовать
- 34. 7) Сумму квадратов итогов по столбцам , деленную на число наблюдений в столбце 8) Сумму квадратов
- 35. 9) Квадрат общего итога, деленный на число всех наблюдений (корректирующий член) 10) Сумму квадратов для столбца
- 36. 14) Остаточную сумму квадратов отклонений для эффекта взаимодействия АВ
- 38. Для оценки значимости фактора А необходимо составить дисперсионное отношение вида
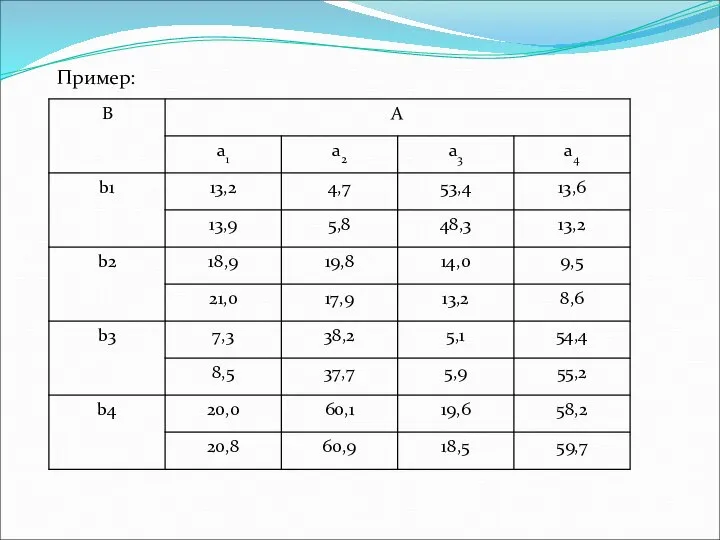
- 39. Пример:
- 40. Многофакторный дисперсионный анализ Латинские и гипер-греко-латинские квадраты. Полным факторным экспериментом(ПФЭ) называют эксперимент, в котором встречаются все
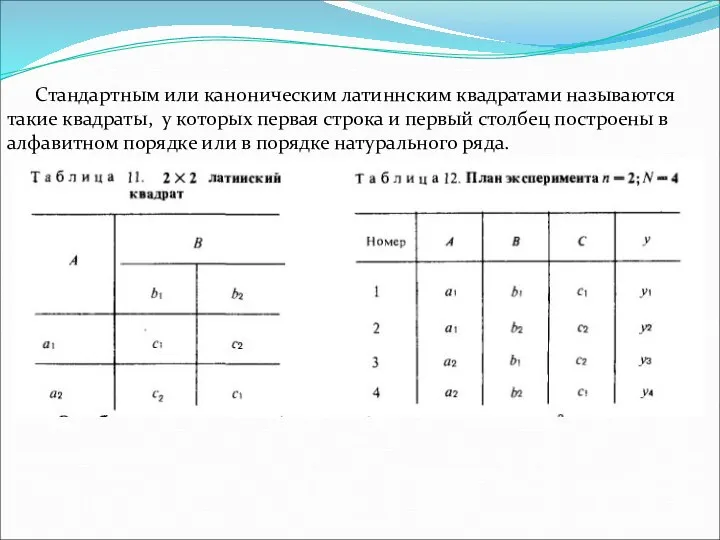
- 41. Стандартным или каноническим латиннским квадратами называются такие квадраты, у которых первая строка и первый столбец построены
- 42. Результат наблюдения, полученный при ПФЭ При применении латинского квадрата предполагают, что результаты взаимодействия незначимы и применяют
- 43. Итоги по латинским буквам 3) Сумму квадратов итогов по строкам, деленную на число наблюдений в строке
- 44. 5)Сумму квадратов итогов по латинским буквам , деленную на число наблюдений, соответствующих каждой букве 6) Квадрат
- 47. Скачать презентацию







































 Основы дисперсионного анализа
Основы дисперсионного анализа Анализ задач и альтернативные методы решений. Мастер-класс
Анализ задач и альтернативные методы решений. Мастер-класс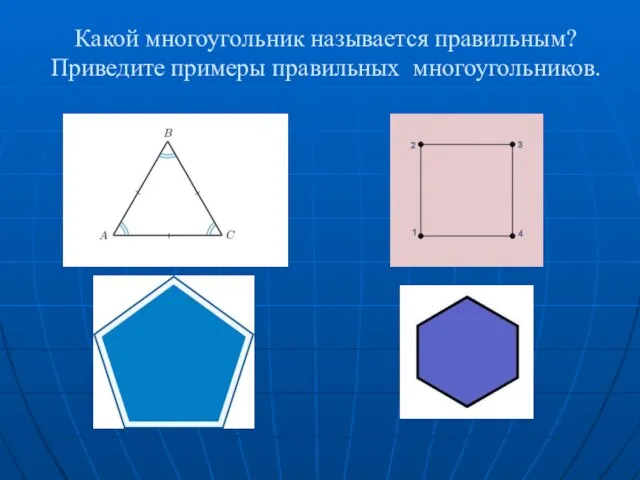 Какой многоугольник называется правильным? Приведите примеры правильных многоугольников
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников Подборка заданий по геометрии за курс 7 класса
Подборка заданий по геометрии за курс 7 класса Предел последовательности. Практическая работа № 24
Предел последовательности. Практическая работа № 24 Построение графиков функций
Построение графиков функций Косинус острого угла прямоугольного треугольника
Косинус острого угла прямоугольного треугольника Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ
Презентация на тему УМНОЖЕНИЕ ДРОБЕЙ  Sıralama algoritmaları
Sıralama algoritmaları Вычисление определенных интегралов (Занятие №6)
Вычисление определенных интегралов (Занятие №6) Презентация на тему Прямоугольные треугольники
Презентация на тему Прямоугольные треугольники  Вероятность. Задачи
Вероятность. Задачи Метод итераций
Метод итераций Сложение и вычитание в пределах 100
Сложение и вычитание в пределах 100 Презентация на тему Нахождение процента от числа
Презентация на тему Нахождение процента от числа  Поверхности второго порядка
Поверхности второго порядка Схемы к задачам
Схемы к задачам Меры измерения времени
Меры измерения времени Презентация на тему Прямоугольный параллелепипед и его свойства
Презентация на тему Прямоугольный параллелепипед и его свойства  Сведения об объеме эфирного времени, затраченного на освещение деятельности политических партий в июле 2020 года
Сведения об объеме эфирного времени, затраченного на освещение деятельности политических партий в июле 2020 года Единицы объёма. Задания
Единицы объёма. Задания Задачи
Задачи Двоичная арифметика
Двоичная арифметика Задачи на дроби
Задачи на дроби Числа и точки на прямой. 5 класс
Числа и точки на прямой. 5 класс Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса
Тригонометрический круг, определение синуса, косинуса, тангенса и котангенса Осевая симметрия
Осевая симметрия Самостоятельная работа по теме Векторы
Самостоятельная работа по теме Векторы