Содержание
- 2. Повторение
- 3. Свойство измерения углов - Каждый угол имеет определенную градусную меру, большую нуля. - Развернутый угол равен
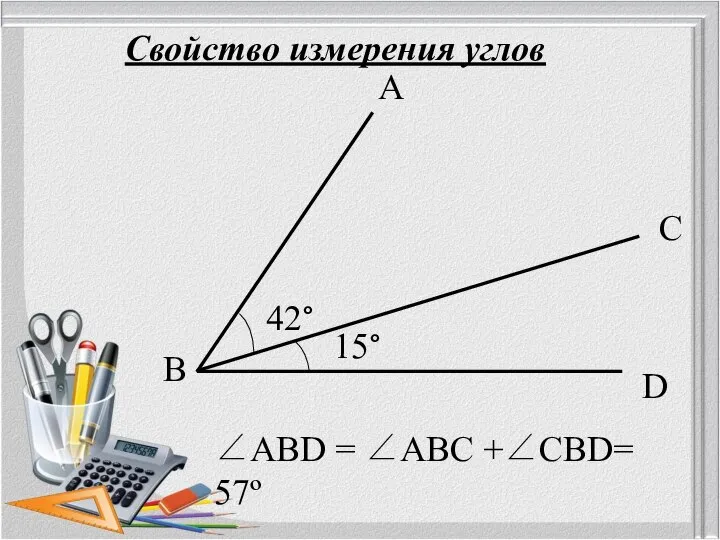
- 4. Свойство измерения углов А В С D 42° 15° ∠АВD = ∠АВC +∠CВD= 57º
- 5. Какие полупрямые называются дополнительными полупрямыми?
- 6. Полупрямой или лучом называется часть прямой, состоящая из всех точек этой прямой, лежащих по одну сторону
- 7. На каком рисунке изображены дополнительные полупрямые? а) б) в)
- 8. Развернутый угол = 180 ° Смежные углы.
- 9. А В О С Смежные углы
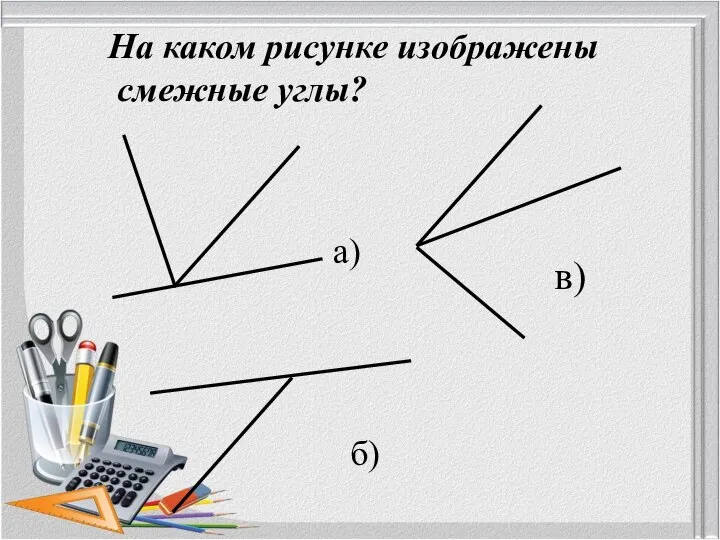
- 10. На каком рисунке изображены смежные углы? а) в) б)
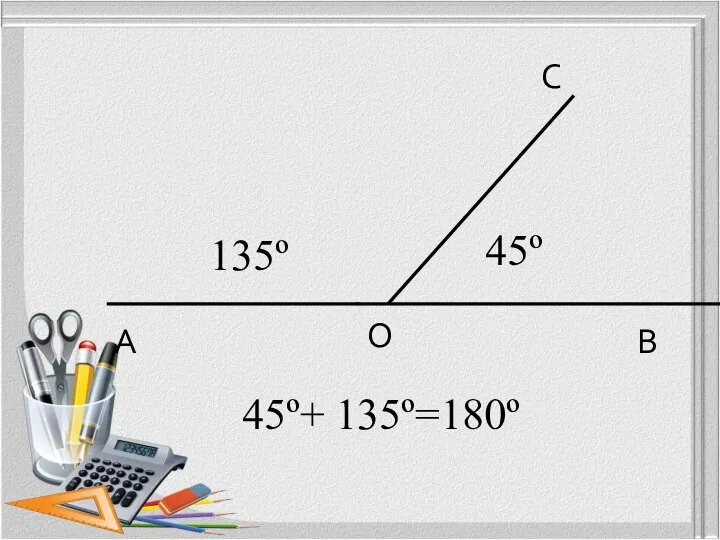
- 11. А В О С 45º+ 135º=180º 45º 135º
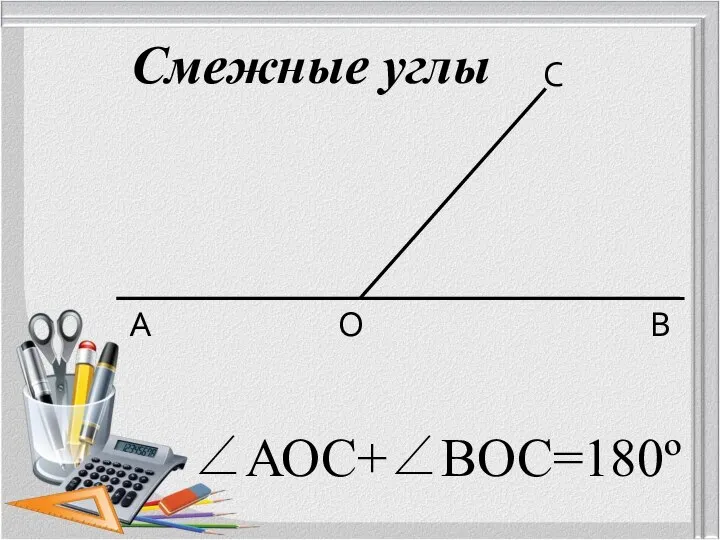
- 12. А В О С ∠АОС+∠ВОС=180º Смежные углы
- 13. Определение. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов
- 14. Сумма смежных углов равна 180 градусам. А В О С ∠АОВ =∠АОС +∠ВОС ∠АОВ – развернутый;
- 15. Задачи
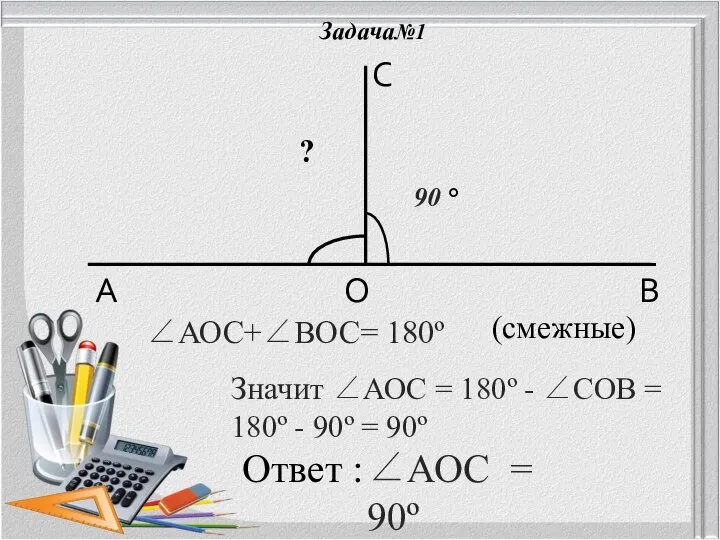
- 16. Задача№1 ? 90 ° А В О С ∠АОС+∠ВОС= 180º (смежные) Значит ∠АОС = 180º -
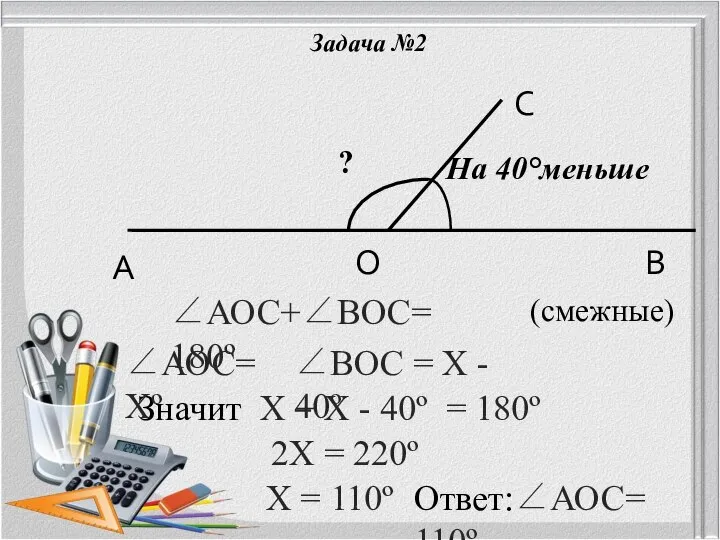
- 17. Задача №2 ? На 40°меньше А В О С ∠АОС+∠ВОС= 180º (смежные) Значит Х + Х
- 18. Какие бывают углы?
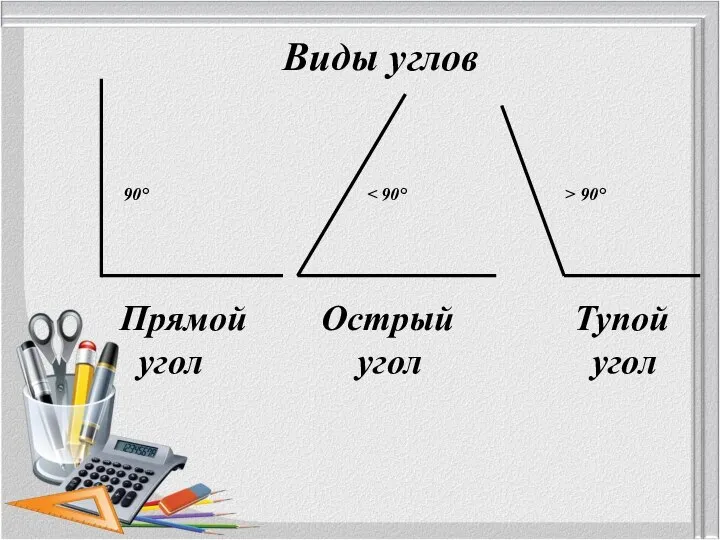
- 19. Виды углов Прямой угол Острый угол Тупой угол 90° > 90°
- 20. Подумай и ответь. 1.Могут ли 2 острых угла быть смежными? 2.Могут ли 2 прямых угла быть
- 21. Вывод: Из двух смежных углов один острый, а другой тупой, или оба - прямые.
- 22. Евклид древнегреческий математик . 365 –300 г.г. до н.э. «Начала» - главный труд Евклида, написанный около
- 23. Следствие из теоремы о сумме смежных углов. 1. Если два угла равны, то и смежные с
- 25. Скачать презентацию















 Объект и пространство
Объект и пространство Математика. Разминка
Математика. Разминка Математическая викторина
Математическая викторина Пирамида. Применение логических законов в решении логических содержательных задач
Пирамида. Применение логических законов в решении логических содержательных задач График функций. Домашняя работа по алгебре
График функций. Домашняя работа по алгебре Смешанные дроби. 5 клас
Смешанные дроби. 5 клас Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики
Алгоритм как один из приемов в формировании учебно-познавательной компетенции на уроках математики З історії геометрії
З історії геометрії Презентация на тему Умножение и деление целых чисел на однозначное число
Презентация на тему Умножение и деление целых чисел на однозначное число  Модуль Начертательная геометрия. Тема 6
Модуль Начертательная геометрия. Тема 6 Игра- тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление
Игра- тренажёр по математике Уроки с Мальвиной. Табличное умножение и деление Презентация на тему История возникновения интеграла
Презентация на тему История возникновения интеграла  Полимино
Полимино Проценты в нашей жизни. Решение задач
Проценты в нашей жизни. Решение задач Решение квадратных неравенств
Решение квадратных неравенств Таблица сложения
Таблица сложения Матрицы
Матрицы Системы показательных уравнений и неравенств
Системы показательных уравнений и неравенств Решение задач на нахождение объемов и площадей поверхностей тел
Решение задач на нахождение объемов и площадей поверхностей тел Оптимизация функций одной переменной
Оптимизация функций одной переменной Презентация на тему Сравнение, сложение, вычитание, умножение, деление десятичных дробей
Презентация на тему Сравнение, сложение, вычитание, умножение, деление десятичных дробей  Определение медианы
Определение медианы Скалярное произведение векторов. Математический диктант
Скалярное произведение векторов. Математический диктант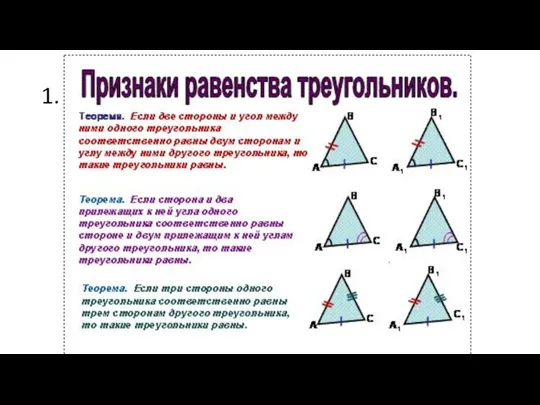 Признаки равенства треугольников
Признаки равенства треугольников Многонранники в нашей жизни
Многонранники в нашей жизни Палички Непера
Палички Непера Умножение на 1 и 0
Умножение на 1 и 0 Правильные многоугольники
Правильные многоугольники