Аксиомы стереометрии и их следствия

Аксиомы планиметрии
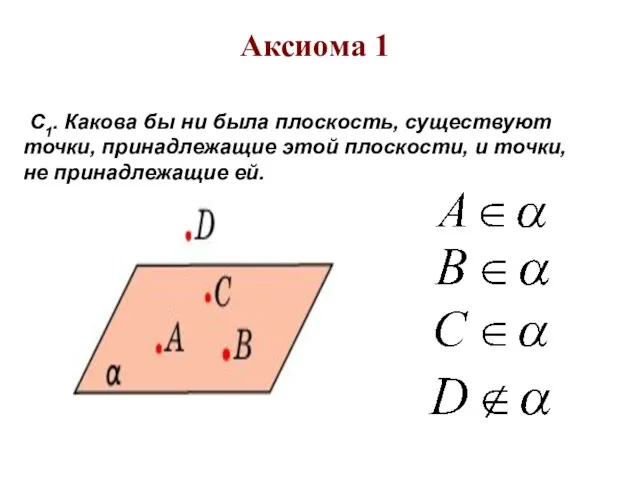
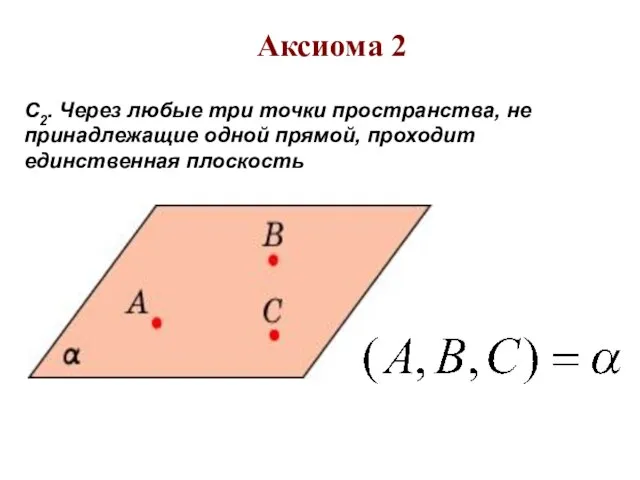
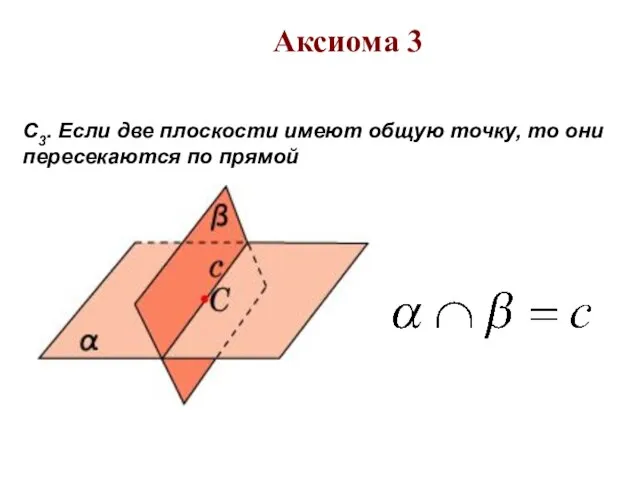
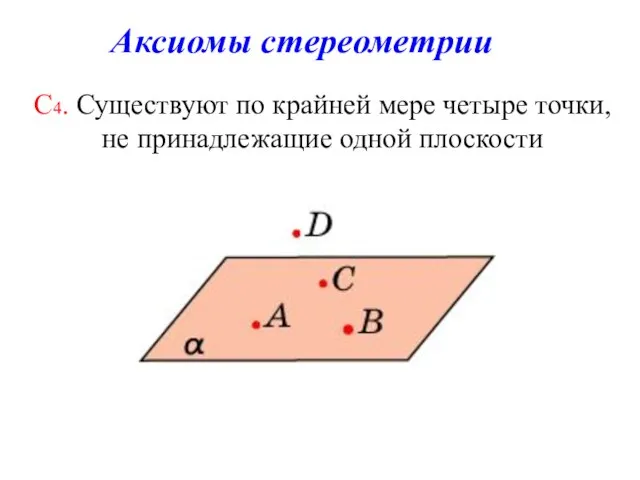
Аксиома 1. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и точки, не принадлежащие ей. Через любые две точки можно провести прямую и только одну.
Аксиома 2. Из трех точек на прямой одна о только одна лежит между двумя другими.
Аксиома 3. Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Аксиома 4. Прямая разбивает плоскость на две полуплоскости.
Аксиома 5. Каждый угол имеет определенную градусную меру, большую нуля. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Аксиома 6. На любой полупрямой от ее начальной точки можно отложить отрезок заданной длины, и только один.
Аксиома 7. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180, и только один.
Аксиома 8. Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой.
Аксиома 9. Через точку, не лежащую на данной прямой можно провести на плоскости не более одной прямой, параллельной данной.
Аксиома – утверждение, принимаемое без доказательства.
Теорема – утверждение, требующее доказательство.

Стереометрия
раздел геометрии, в котором
изучаются свойства фигур
в пространстве
Основные фигуры в пространстве:
А
Точка
а
Прямая
Плоскость

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …

Геометрические тела:
Куб
Пирамида
Конус

Геометрические понятия
Плоскость – грань
Прямая – ребро
Точка – вершина
вершина
грань
ребро

Аксиома 1
С1. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.

С2. Через любые три точки пространства, не принадлежащие одной прямой, проходит единственная плоскость
Аксиома 2

С3. Если две плоскости имеют общую точку, то они пересекаются по прямой
Аксиома 3

С4. Существуют по крайней мере четыре точки, не принадлежащие одной плоскости
Аксиомы стереометрии

A5. На любой плоскости выполняются все аксиомы планиметрии
Аксиомы стереометрии

Сколько прямых проходит через две точки пространства?
Сколько плоскостей проходит через три точки пространства?
Сколько общих точек могут иметь две плоскости?
Верно ли, что если окружность имеет с плоскостью две общие точки, то окружность лежит в этой плоскости?
Ответьте на вопросы.