Содержание
- 2. Обратные тригонометрические функции
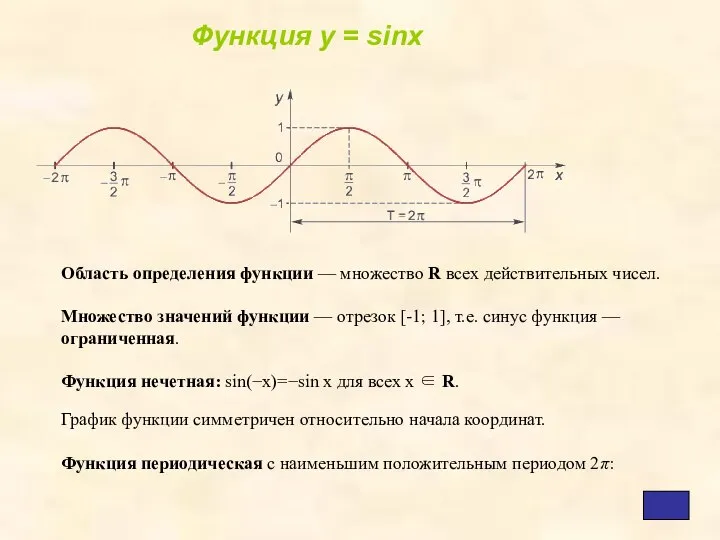
- 3. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1],
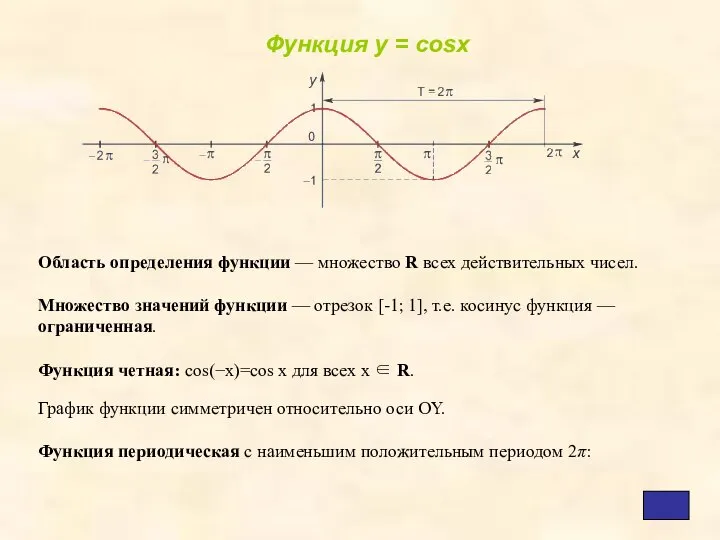
- 4. Область определения функции — множество R всех действительных чисел. Множество значений функции — отрезок [-1; 1],
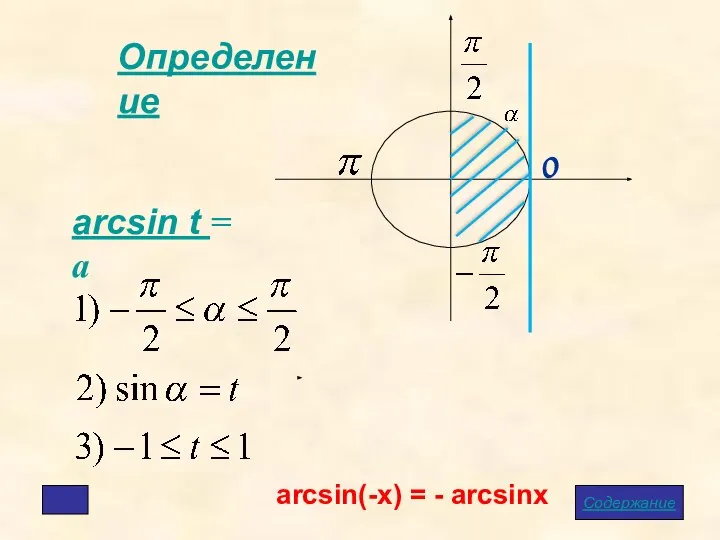
- 5. Определение arcsin t = a arcsin(-x) = - arcsinx Содержание
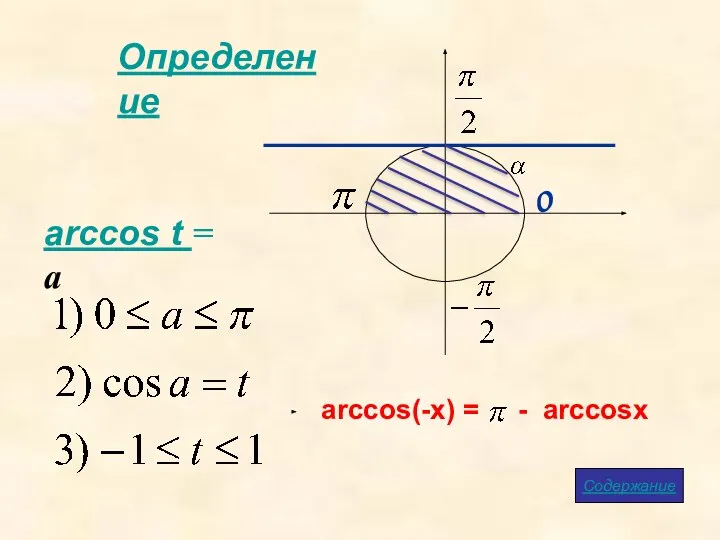
- 6. Определение arccos t = a Содержание arccos(-x) = - arccosx
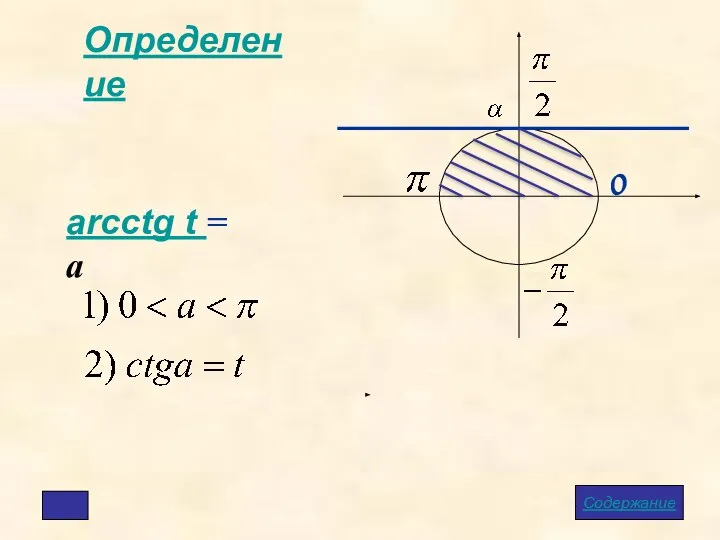
- 7. Определение arctg t = a Содержание
- 8. Определение arcctg t = a Содержание
- 9. у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция у
- 10. у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у = arcсos x
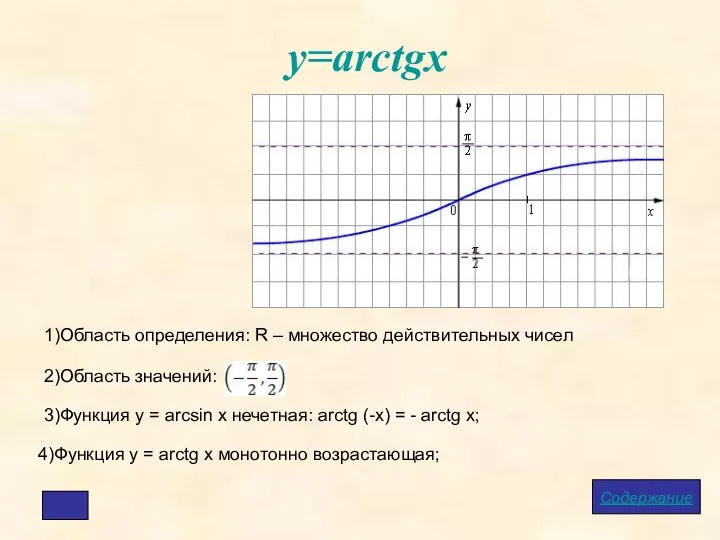
- 11. у=arctgx Содержание 1)Область определения: R – множество действительных чисел 2)Область значений: 3)Функция у = arcsin x
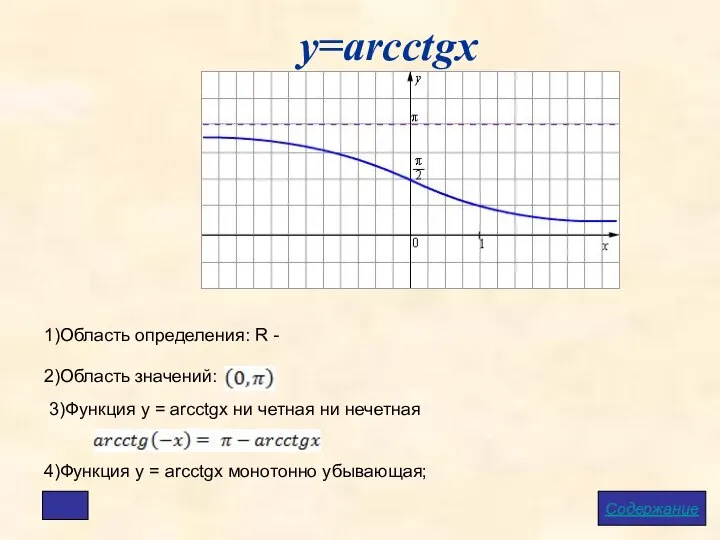
- 12. у=arcctgx Содержание 1)Область определения: R - 2)Область значений: 4)Функция у = arcсtgx монотонно убывающая; 3)Функция у
- 13. Работаем устно Содержание arcsin(-x) = - arcsinx arccos(-x) = - arccosx
- 14. Работаем устно Содержание arctg(-x) = - arctgx arcctg(-x) = - arcctgx
- 16. Скачать презентацию

![у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1081760/slide-8.jpg)
![у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1081760/slide-9.jpg)


 ОГЭ. Приемы решения практико-ориентированных задач
ОГЭ. Приемы решения практико-ориентированных задач Литр. Задачи
Литр. Задачи Презентация на тему Зарождение и история геометрии
Презентация на тему Зарождение и история геометрии  Презентация на тему Устный счет до десяти
Презентация на тему Устный счет до десяти  Алгебра. Города
Алгебра. Города Урок начинается. Занимательная математика
Урок начинается. Занимательная математика Площадь прямоугольника
Площадь прямоугольника Презентация на тему Доли. Обыкновенные дроби (5 класс)
Презентация на тему Доли. Обыкновенные дроби (5 класс)  Свойства сложения и умножения - Презентация_
Свойства сложения и умножения - Презентация_ Презентация на тему СРАВНЕНИЕ ДРОБЕЙ
Презентация на тему СРАВНЕНИЕ ДРОБЕЙ  Задачи на построение
Задачи на построение Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Булева алгебра. Семинар №2
Булева алгебра. Семинар №2 Число е. 2,7182818284…
Число е. 2,7182818284… Презентация на тему Скорость, время, расстояние
Презентация на тему Скорость, время, расстояние  Презентация на тему Деление положительных и отрицательных чисел
Презентация на тему Деление положительных и отрицательных чисел  Проценты. ОГЭ и ЕГЭ
Проценты. ОГЭ и ЕГЭ Деление с остатком
Деление с остатком 797821
797821 Геометрическая оптика. Изображение предметов при преломлении света. Линзы
Геометрическая оптика. Изображение предметов при преломлении света. Линзы Сложение целых чисел
Сложение целых чисел Модуль. Определение. Свойства. Геометрический смысл модуля
Модуль. Определение. Свойства. Геометрический смысл модуля Многоугольники
Многоугольники 38 попугаев
38 попугаев Решение квадратных уравнений
Решение квадратных уравнений Диференціальні рівняння
Диференціальні рівняння ОГЭ 2019. Модуль Геометрия
ОГЭ 2019. Модуль Геометрия Нечеткие дифференциальные уравнения
Нечеткие дифференциальные уравнения