Оценка вероятности поражения обслуживающего персонала при подрыве РКН

Опасность особенно велика в начальный период полета, когда большая часть топлива еще не сгорела. На более поздней стадии полета топлива остается меньше, а горящие куски проходят большой путь, прежде чем удариться о поверхность земли. Поэтому при анализе ситуации аварийного подрыва одним из определяющих параметров является момент его осуществления.
Степень риска для обслуживающего персонала характеризуется вероятностью поражения человека, которая, в свою очередь, определяется математическим ожиданием несчастного случая и позволяет предсказать возможное число этих случаев, если произошло падение обломков и топлива на землю и эти обломки взорвались (дефлагировали).

Для правильной оценки математического ожидания числа несчастных случаев необходимо учитывать следующие факторы, которые могут быть сгруппированы в две категории:
– характеристики ЛА, которые определяют расчетную дальность, вероятность возникновения неисправностей в полете, количество и тип топлива, а также характер разлета частей ЛА под действием аэродинамических сил и в результате срабатывания системы аварийного подрыва;
– характеристики внешних условий, которые определяются расположением стартовой позиции и азимутом пусков, направлением и скоростью ветра, распределением обслуживающего персонала вблизи трассы полета.

20.2. Определение математического ожидания несчастного случая.
Модель строится в предположении, что подверженная опасность падения обломков территория имеет зоны с различной степенью защищенности:
S1 – территория под открытым небом;
S2 – территория легких построек;
S3 – территория фундаментальных зданий.
Пусть в пределах области S имеется n уровней защищенности, а площади, характеризуемые этими уровнями, обозначаются через Si(i=1,2,...,n); Ni – число людей, находящихся в области Si и имеющих уровень защищенности i-й зоны, а Рij – вероятность того, что j-й обломок ЛА упадет на площадь Si. Этому обломку соответствует n зон несчастного случая – по одной для каждого уровня защищенности. Под зоной несчастного случая подразумевается площадь, окружающая точку падения обломка, граница которой является геометрическим местом точек, вероятность несчастных случаев в которых равна 0,5.

Математическое ожидание несчастного случая на площади Sj от j-го обломка ЛА определяется по формуле:
Если просуммировать это выражение по всем обломкам j и по всем уровням защищенности i, то получим математическое ожидание несчастного случая на всей территории от действия всех обломков:
Если S мало, то вероятность падения j-го обломка в заданную точку будет
одинакова по всей площади S и составит:
а уравнение (20.2) примет вид:
(20.4)
(20.1)
(20.3)
(20.2)

Если ввести обозначения
то можно выражение (20.2) записать так:
(20.5)
где – количество обслуживающего персонала,
находящегося на площади S;
– суммарная площадь зон несчастного случая.
Следует отметить, что размеры области, для которой справедливо равенство Р = Рij, зависят от расположения ее относительно точки запуска ЛА и расчетной траектории полета этого аппарата.

20.3. Определение площади зоны несчастного случая от осколков.
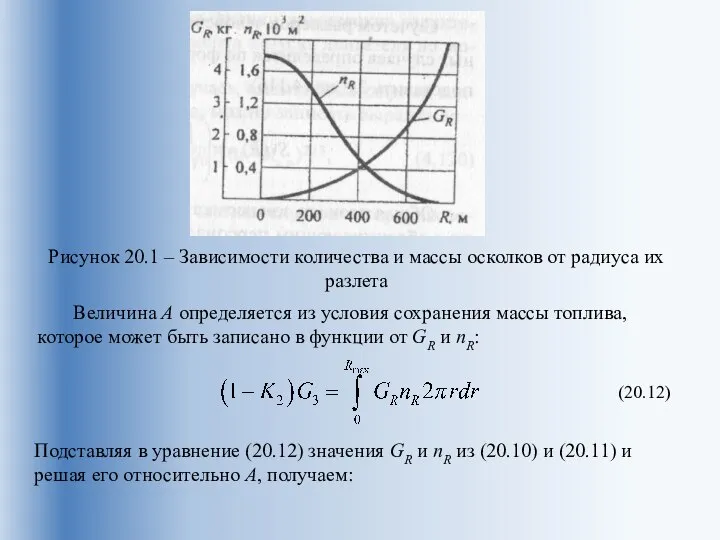
Зоной несчастного случая является та область, на которой человек мог бы получить травму от прямого попадания падающего или рикошетирующего обломка ЛА или избыточного давления, явившегося следствием взрыва ступени ЛА. Эта зона является функцией времени, так как она уменьшается с увеличением времени полета из-за выгорания топлива.
Влияние присутствия человека на величину площади зоны несчастного случая, соответствующей отдельному осколку, может быть учтено увеличением этой зоны на величину площади, занимаемой стоящим человеком равной 0,186 м2. Если осколок очень мал и падает на площадь 0,186 м2, то все равно произойдет несчастный случай, т. е. минимальная зона несчастного случая 0,186 м2. Если осколок имеет площадь большую, занимаемой человеком, то за пределами этой зоны на расстоянии 0,61 м от ее границы, часть тела человека будет поражена.
Следовательно, зона несчастного случая определяется формулой:
(20.6)

20.4. Определение площади зоны несчастного случая от ударной волны.
Для определения избыточного давления в зависимости от расстояния и массы тротила существует несколько эмпирических формул. Одна из них, формула Кингери, выведена с помощью изменения давления при взрывах 5...100 т тротила. Радиус, на котором ожидается данное значение максимального избыточного давления, определяется по формуле:
(20.7)
Избыточное давление 14,7 КПа повреждает барабанные перепонки у человека, 35 КПа – повреждает легкие, а 70 КПа – может оказаться смертельным.
Если под несчастным случаем понимать повреждение барабанных перепонок, то площадь зоны несчастного случая определится из общей формулы:
подстановкой вместо R значения
(20.9)
(20.9)
(20.8)

20.5. Определение площади зоны несчастного случая от горящих осколков топлива.
Оставшаяся невзорвавшаяся часть топлива (1 – K2)G3 разбрасывается вокруг точки падения в виде горящих осколков.
Осколки имеют различную массу в зависимости от радиуса разлета, причем с увеличением радиуса масса осколков увеличивается. Средняя масса осколков на расстоянии R от центра взрыва определяется по формуле:
GR = K3R2 (20.10)
Количество осколков, приходящееся на единицу площади, с увеличением R будет уменьшаться и может быть определено из выражения:
(20.11)
Вид представленных зависимостей (20.10) и (20.11) изображен на рисунке 20.1.

Рисунок 20.1 – Зависимости количества и массы осколков от радиуса их разлета
Величина А определяется из условия сохранения массы топлива, которое может быть записано в функции от GR и nR:
(20.12)
Подставляя в уравнение (20.12) значения GR и nR из (20.10) и (20.11) и решая его относительно А, получаем:

(20.13)
Анализ фотоснимков показывает, что большинство несгоревших кусков – это прямоугольные параллелепипеды с размерами lxlx2l. Поэтому, обозначив через ρ удельный вес топлива, будем иметь:
(20.14)
Подставляя в уравнение (20.14) значение G3 из (20.10) и имея в виду, что зона несчастного случая имеет размеры в плане 2lxl, получаем среднюю площадь, занимаемую одним осколком:
или
(20.15)
С учетом размеров человеческого тела площадь зоны несчастных случаев
определится по формуле (20.6), если в нее вместо подставить 2l2 из (20.15):
(20.16)