Слайд 2Движения
Симметрия
Параллельный
перенос
Поворот
Осевая
симметрия
Центральная
симметрия
Слайд 3Осевая симметрия
Определение
Осевая симметрия –это отображение плоскости на себя, при котором
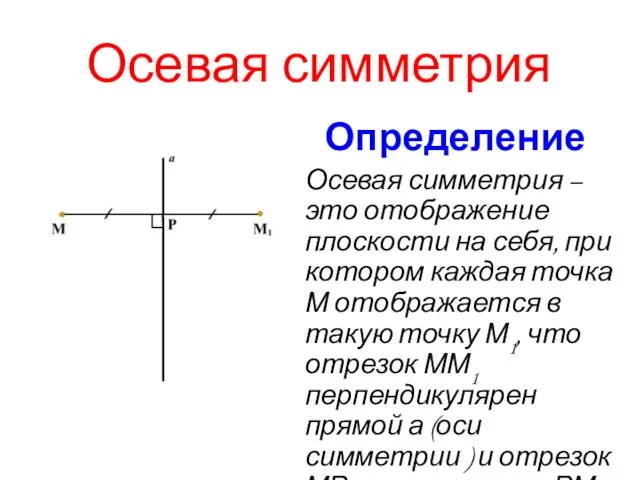
каждая точка М отображается в такую точку М1, что отрезок ММ1 перпендикулярен прямой а (оси симметрии ) и отрезок МР равен отрезку РМ1.
Слайд 4Построение
Пусть а – ось симметрии.
∆АВС – произвольный. Проведем перпендикуляр ВР к
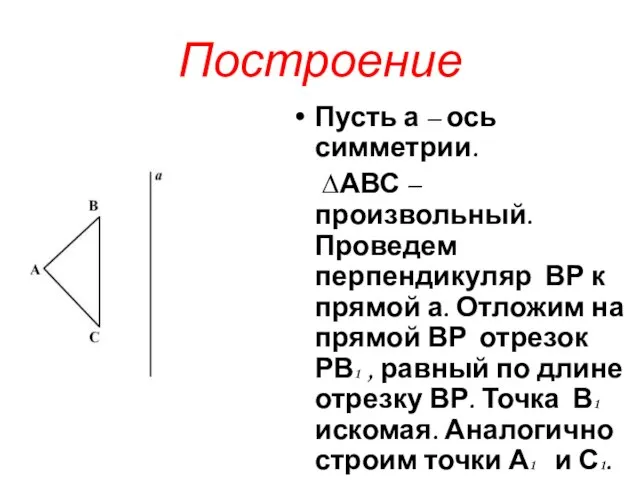
прямой а. Отложим на прямой ВР отрезок РВ1 , равный по длине отрезку ВР. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С 1 симметричен ∆АВС относительно прямой а.
Слайд 7Задача
Сколько осей симметрии имеет равносторонний треугольник?
Сколько осей симметрии имеет квадрат?

Сколько осей симметрии имеет ромб, не являющийся квадратом?
Начертите и убедитесь в правильности своего ответа
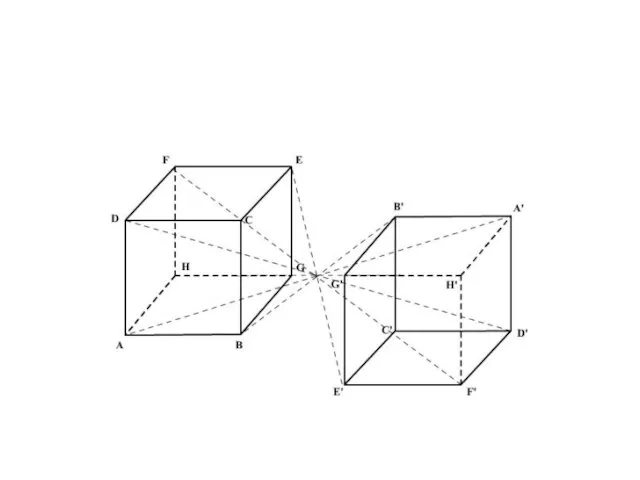
Слайд 8Центральная симметрия
Определение
Центральная симметрия –это отображение плоскости на себя , при котором
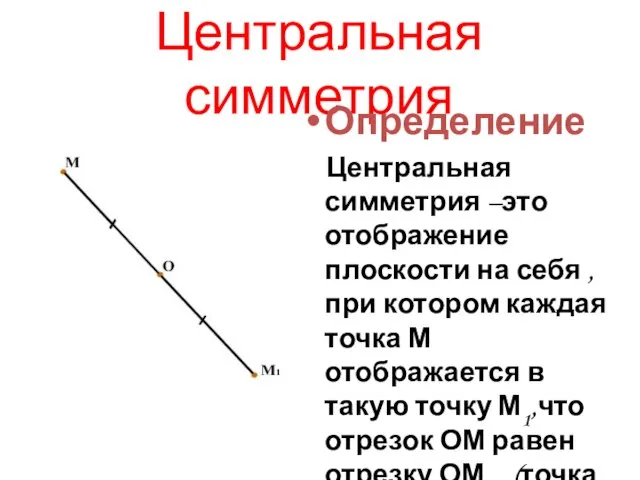
каждая точка М отображается в такую точку М1,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).
Слайд 9Построение
Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч ВО. Отложим
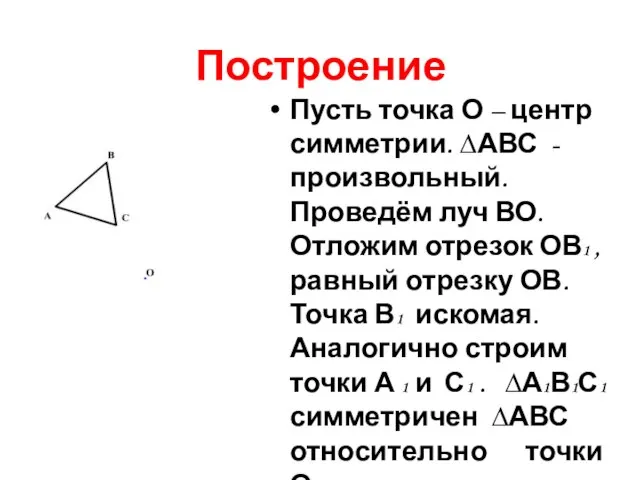
отрезок ОВ1 , равный отрезку ОВ. Точка В1 искомая. Аналогично строим точки А 1 и С1 . ∆А1В1С1 симметричен ∆АВС относительно точки О.
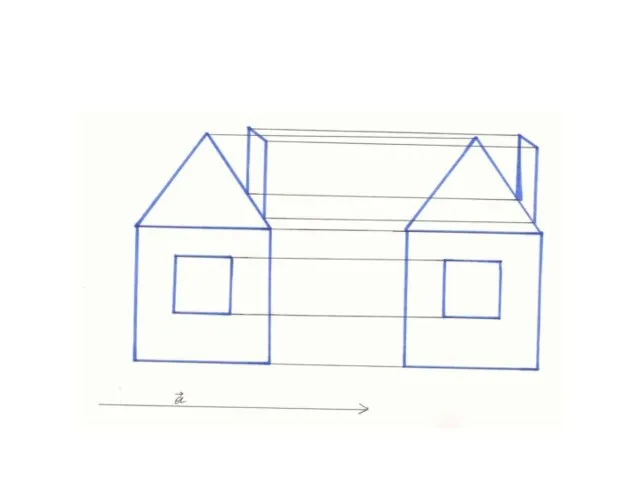
Слайд 12Параллельный перенос
Определение.
Параллельный перенос – это отображение плоскости на себя, при котором
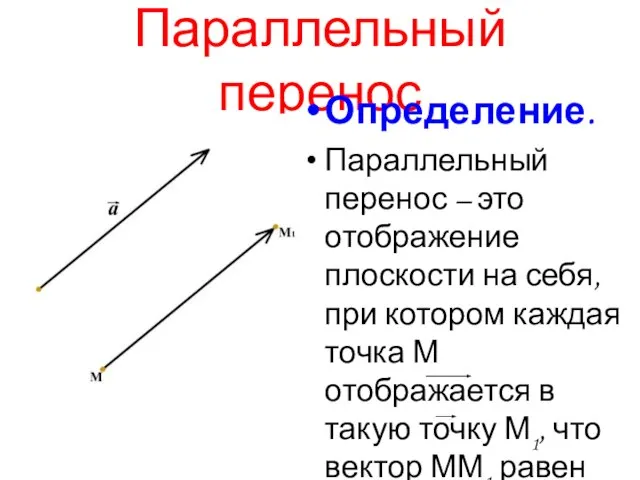
каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а.
Слайд 13Построение
Пусть дан вектор а. ∆АВС произвольный. От точки В отложим вектор ВВ1
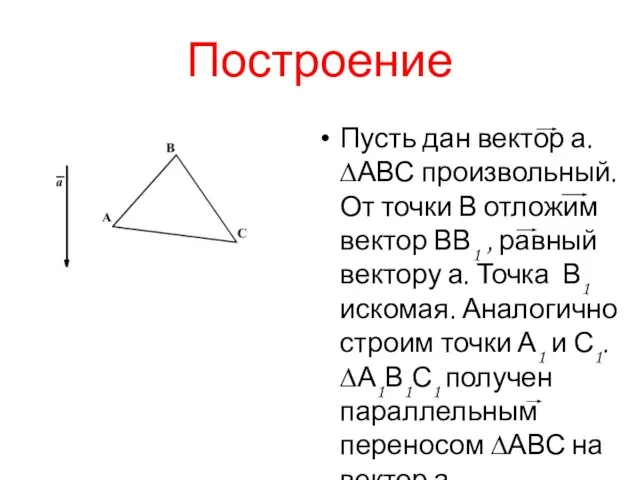
, равный вектору а. Точка В1 искомая. Аналогично строим точки А1 и С1. ∆А1В1С1 получен параллельным переносом ∆АВС на вектор а.
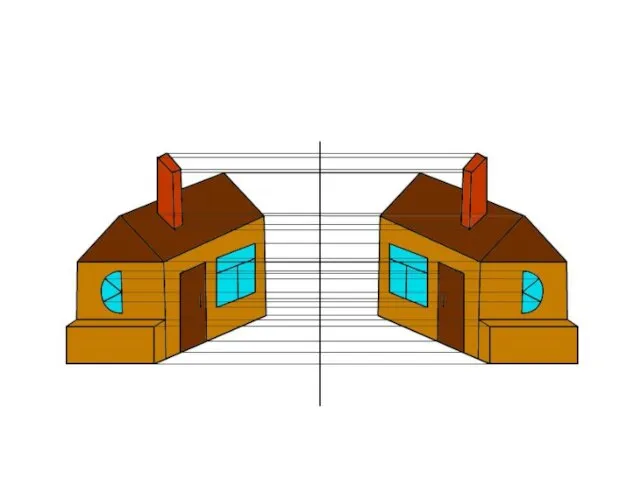
Слайд 16Движение в архитектуре.
Определить вид движения.
АКВИДУК

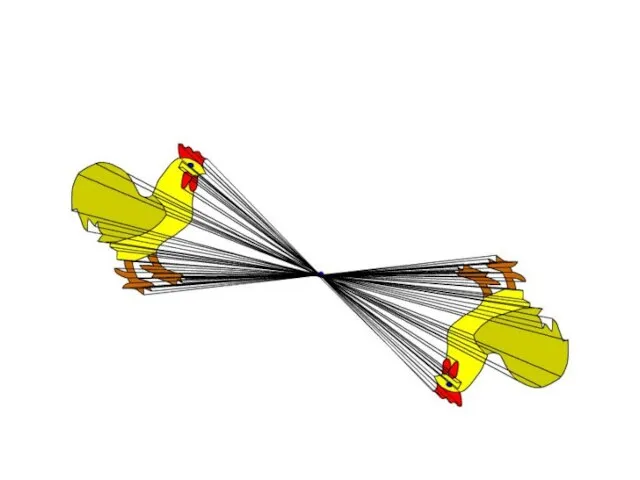
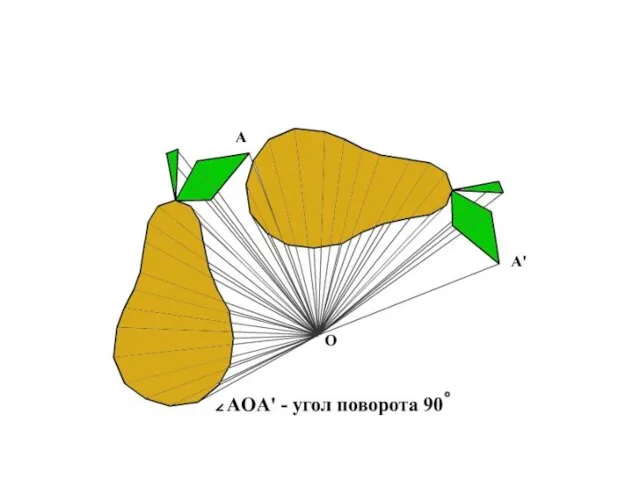
Слайд 17Поворот
Определение
Поворот плоскости вокруг точки О на угол - это
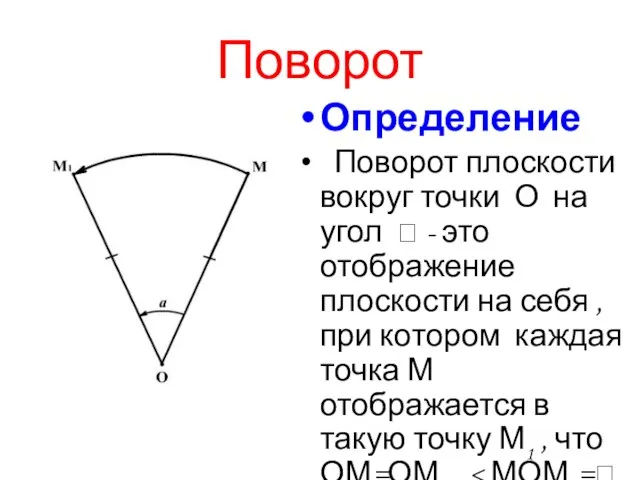
отображение плоскости на себя , при котором каждая точка М отображается в такую точку М1 , что ОМ=ОМ1 , < МОМ1=.
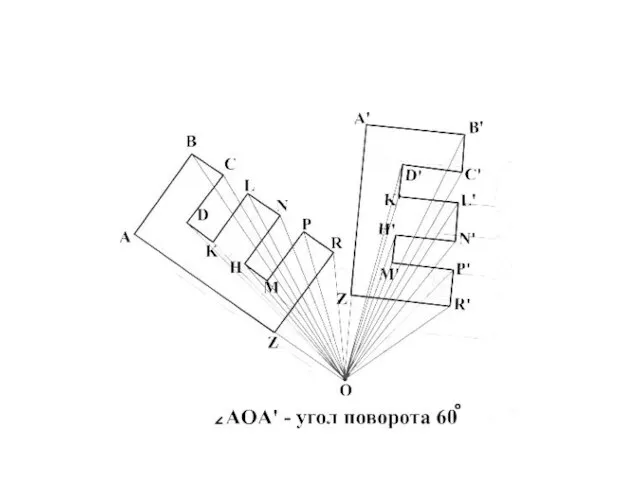
Слайд 18Построение
Пусть О – центр поворота, =90º, ∆АВС – произвольный. Проведём отрезок АВ,
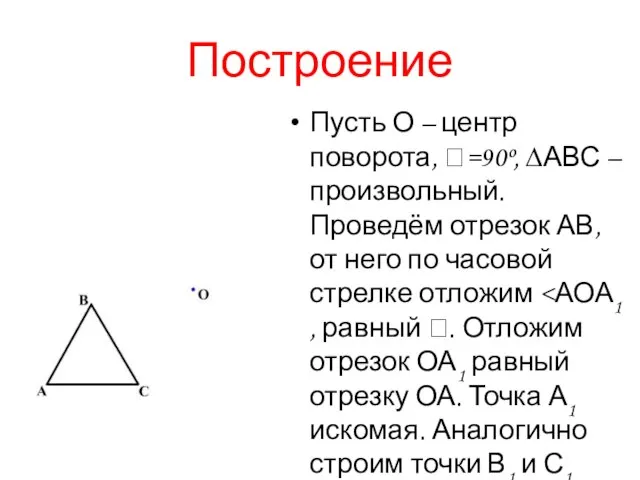
от него по часовой стрелке отложим <АОА1 , равный . Отложим отрезок ОА1 равный отрезку ОА. Точка А1 искомая. Аналогично строим точки В1 и С1
Слайд 21Вопросы
Определить вид симметрии.
Что вам приходилось встречать в природе из известных видов симметрии?

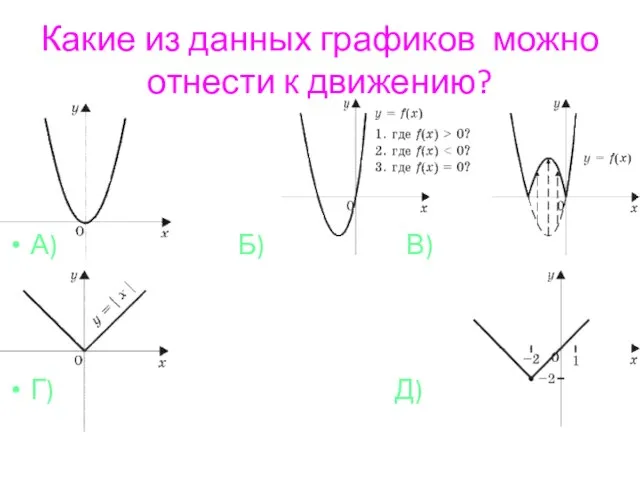
Слайд 28Какие из данных графиков можно отнести к движению?
А) Б) В)
Г) Д)
Слайд 29Выполнение
практической работы
Выполни работу на тот вид движения, который тебе понравился.

Слайд 30Выбери себе задание:
работа в парах
С-11, вар. Б1,2 - №1
С-12, вар. А1,2

- №1
С-12, вар. Б1,2 - №2























 Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша
Геометрическое моделирование объекта шифрования на основе точечного исчисления Балюбы-Найдыша Приемы вычитания с переходом на десяток
Приемы вычитания с переходом на десяток Функция y=ctg x. График
Функция y=ctg x. График Матрицы и определители
Матрицы и определители Дифференциальное исчисление в нормированных пространствах
Дифференциальное исчисление в нормированных пространствах Элементы теории обобщенных функций
Элементы теории обобщенных функций ЛЕКЦИЯ_6
ЛЕКЦИЯ_6 Механический смысл производной. Задания для устного счета
Механический смысл производной. Задания для устного счета Умножение. Координаты точки
Умножение. Координаты точки Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества
Множества и операции над ними. Пустое множество. Способы задания множеств. Подмножества данного множества Решение задач на дроби
Решение задач на дроби Равенство
Равенство Случаи вычитания 11-
Случаи вычитания 11- Веселые ромашки
Веселые ромашки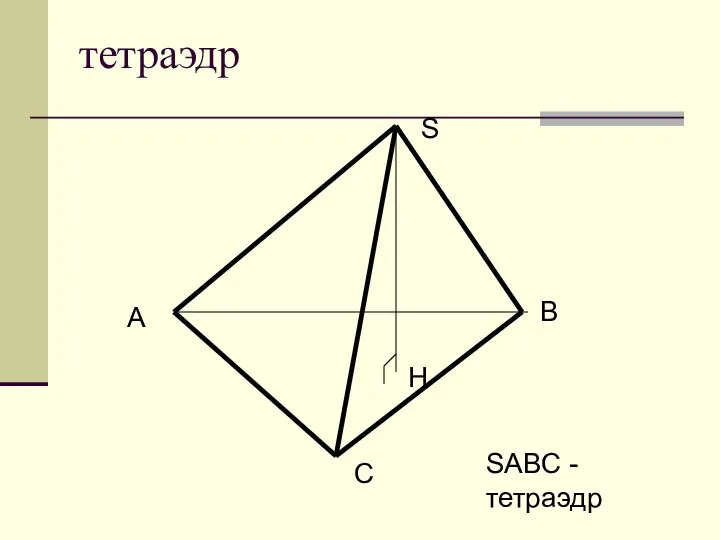 Тетраэдр
Тетраэдр Векторы. Направление вектора
Векторы. Направление вектора Изоморфные графы
Изоморфные графы Функция распределения дискретной случайной величины
Функция распределения дискретной случайной величины Игры. Памятка
Игры. Памятка Многоугольники в жизни
Многоугольники в жизни Методический материал по алгебре
Методический материал по алгебре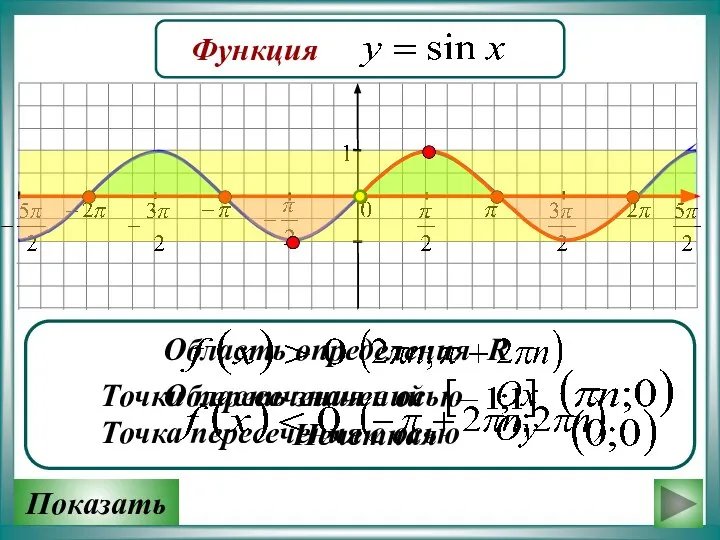 График функции y = sin x
График функции y = sin x Путешествие по морям
Путешествие по морям Возведение двучлена в любую натуральную степень
Возведение двучлена в любую натуральную степень Площадь параллелограмма
Площадь параллелограмма Смежные углы
Смежные углы Сложение целых чисел
Сложение целых чисел Понятие интеграла
Понятие интеграла