Содержание
- 2. Любое число можно отметить точкой на координатной прямой. Каждой точке на координатной прямой соответствует какое-то число.
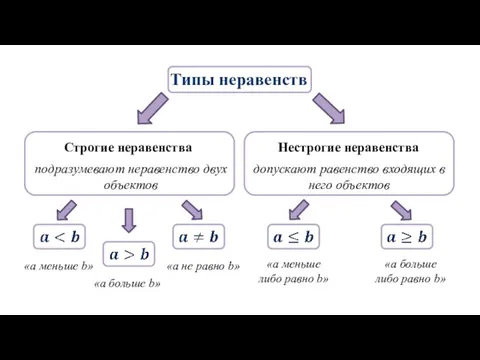
- 3. Типы неравенств Строгие неравенства Нестрогие неравенства подразумевают неравенство двух объектов допускают равенство входящих в него объектов
- 4. Виды числовых промежутков «интервал от минус двух до трех» «отрезок от минус двух до трех»
- 5. «полуинтервал от минус двух до трех, включая минус два» «полуинтервал от минус двух до трех, включая
- 6. Множество действительных чисел изображается всей координатной прямой. Его называют числовой прямой. Виды числовых промежутков «промежуток от
- 7. Виды числовых промежутков «числовой луч от трех до плюс бесконечности» «числовой луч от минус бесконечности до
- 8. Виды числовых промежутков «открытый числовой луч от трех до плюс бесконечности» «открытый числовой луч от минус
- 9. Если граничная точка в промежуток не входит, то на координатной прямой ее изображают пустой точкой и
- 10. интервал числовой отрезок полуинтервал полуинтервал числовой луч числовой луч открытый числовой луч открытый числовой луч
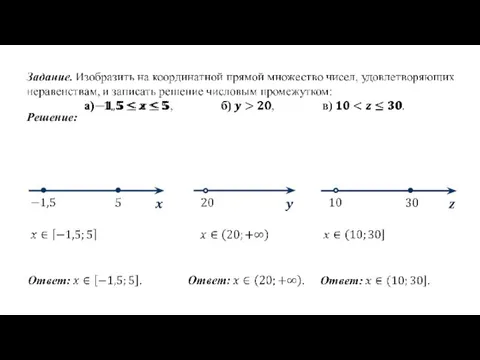
- 11. Решение:
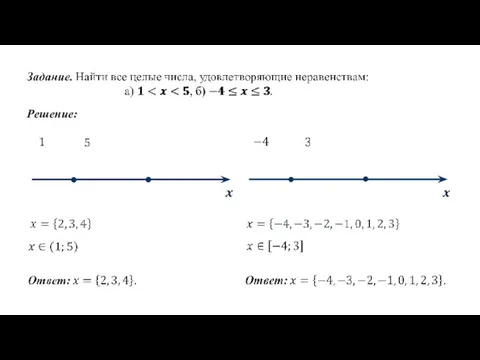
- 12. Решение:
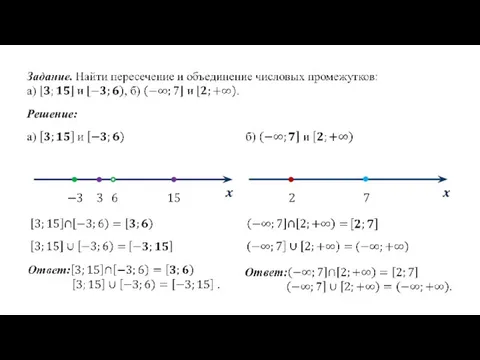
- 13. Решение:
- 14. Решение:
- 15. Интервал – это множество чисел, удовлетворяющих условию ? Отрезок – это множество чисел, удовлетворяющих условию ?≤?≤?
- 16. Решение неравенств с одной переменной
- 18. Такие неравенства называют неравенством с одной переменной или неравенством с одним неизвестным. – неверное числовое неравенство.
- 20. Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое неравенство. Решить
- 21. Свойства числовых неравенств: Если в неравенстве перенести слагаемое из одной части в другую с противоположным знаком,
- 22. Решение:
- 23. Линейные неравенства с одной переменной
- 24. Неравенство такого вида либо не имеют решений, либо их решением является любое число. Например: нет решений
- 26. Скачать презентацию













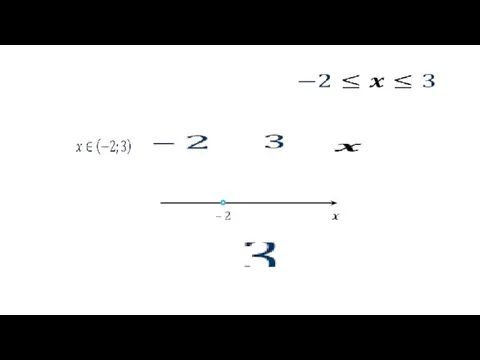





 Решение текстовых задач на ЕГЭ
Решение текстовых задач на ЕГЭ Это страшное слово: Параметр
Это страшное слово: Параметр Работа по формированию математических понятий
Работа по формированию математических понятий Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс
Вычисление значений числовых выражений с действиями разной степени. Проверка деления умножением. 3 класс Внеклассное мероприятие. 5 класс
Внеклассное мероприятие. 5 класс Открытый урок по алгебре в 8 классе
Открытый урок по алгебре в 8 классе Цифровой образовательный ресурс по алгебре. 8 класс
Цифровой образовательный ресурс по алгебре. 8 класс Поворот. Пример построения треугольника
Поворот. Пример построения треугольника Решение задач на вычисление площадей четырехугольников
Решение задач на вычисление площадей четырехугольников Формулы сокращенного умножения и их применение
Формулы сокращенного умножения и их применение Построение треугольника
Построение треугольника Свойства параллельных прямых
Свойства параллельных прямых Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Lecture 7
Lecture 7 Математична статистика
Математична статистика Параллельный перенос
Параллельный перенос Курс по математике ОГЭ 2021
Курс по математике ОГЭ 2021 Система управління технологічного процесу приготування розчинів для піроксилінових порохів
Система управління технологічного процесу приготування розчинів для піроксилінових порохів Задачи на подобие треугольников
Задачи на подобие треугольников Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності
Оптимізація процесів прийняття рішень при плануванні транспортних перевезень в умовах невизначеності Корни. Формулы
Корни. Формулы Многочлен. Задача
Многочлен. Задача Нуль без палочки. Математический турнир
Нуль без палочки. Математический турнир Квадратный трёхчлен и его корни
Квадратный трёхчлен и его корни Высота. Длина. Площадь
Высота. Длина. Площадь Развёртка, как основа объёмной конструкции
Развёртка, как основа объёмной конструкции Алгоритмы на графах
Алгоритмы на графах Функции y=x(-n), их свойства и графики
Функции y=x(-n), их свойства и графики