Определение и способы задания числовой функции

Переменная х – независимая переменная или аргумент.
Переменная у – зависимая переменная.
Область определения обозначают Х или D(у).
Область значений – Y или Е(у).

Функция считается заданной, если указано правило, согласно которому по любому произвольно выбранному значению х ∊ D(f) можно вычислить соответствующее значение у.
Аналитический способ

Функции, заданные аналитически:
y = 2x
y = x2
у = 5х – 6

Преимущества: всегда можно найти значение функции с определенной точностью и быстро.
Недостатки: по формуле невозможно определить характер изменения функции.

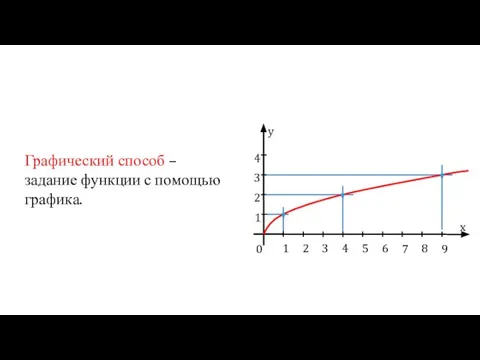
Графический способ –
задание функции с помощью графика.

Кардиограф
Барограф
Термограф

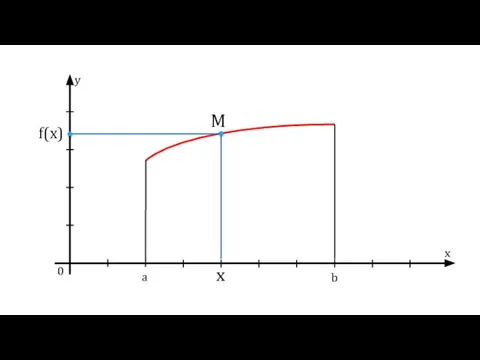
y
x
0
a
b
x
f(x)

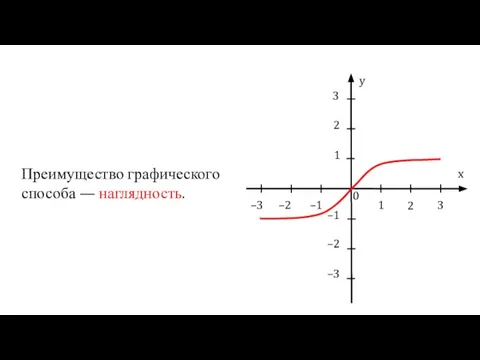
Преимущество графического
способа — наглядность.

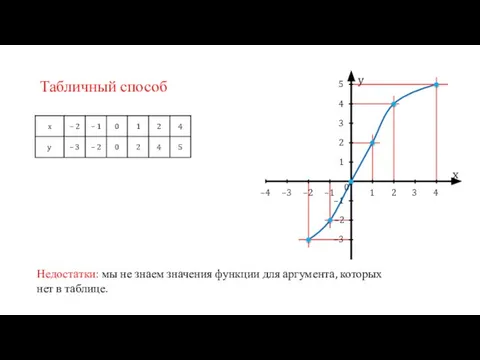
Табличный способ
Недостатки: мы не знаем значения функции для аргумента, которых нет в таблице.
y
x
0
1
2
3
4
1
2
3
4
5
–1
–2
–3
–4
–1
–2
–3

Словесный способ
Правило задания функции описывается словами.
Пример: у = 3х –
каждому действительному значению аргумента х ставится в соответствие его утроенное значение.